The magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
A
tan−1(2−√3−12+√3+1)
B
tan−1(1−√3+11+√3+√2)
C
tan−1(()1−√3−√2))1+√3−√2)
D
tan−1(1+√3+√21−√3+√2
Video Solution
Text Solution
The correct Answer is:B
Let OA+OB=OC=P
Componet fo −−→OA along x-axis
=Pcos30∘=P√32
Component of −−→OA along y-xis =Psin30∘=P2
Component of −−→OB along x-axis=Pcos60∘=P2.
Component of OB along y-axis<br>=- P sin 60^2 =( -P sqrt 3)/2 <br>Compo≠ntof vec (OP)alongx−aξs<br> =- P sin 45^@= (-P)/(sqrt 2)<br>Compo≠ntof vec (OC)alongy−aξs<br> P= cos 45^@ = P/(sqrt 2)<br>∴x−compo≠ntof vec (OA) + vec (OB) - vec (OC),<br> | vec P_x| = (Psqrt 3)/2 + P/2 - ( (-P)/(sqrt 2)) = P/2 (sqrt 3 + 1 + sqrt2)<br>y−compo≠ntof vec (OA) +vec (OB) - vec (OC),<br> | vec P_y| = P/2+ ((-P sqrt 3)/2) - P/(sqrt 2) = P/2 (-1 sqrt 2)<br>Ang≤of vec (OA) + vec (OB)- vec (OC)withx−aξsis<br> theta = tan^(-1) (P_y//P_x)= tan^(-1) [(P/2(1 - sqrt 3 - sqrt 2))/(P/2 (1+ sqrt + sqrt 2))]<br>= tan^(-1)(1−√3−√21+√3+√2).
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 NCERT multiple Choice10videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 4 NCERT Integer type4videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 NCERT multiple15videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
The resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure is
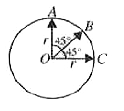 ArB2rCr(1+√s)Dr(√2−1)
ArB2rCr(1+√s)Dr(√2−1) - Question 2 - Select One
Two vector →A and →B have equal magnitudes. Then the vector →A+→B is perpendicular :
A→A×→BB→A−→BC3→A−3→BDAll of these - Question 3 - Select One
Let O, O' and G be the circumcentre, orthocentre and centroid of a ΔABC and S be any point in the plane of the triangle.
Statement -1: −−−→O'A+−−−→O'B+−−−→O'C=2−−−→O'O
Statement -2: −→SA+−−→SB+−−→SC=3−−→SGAStatement - 1 is True, Statement - 2 is True , Statement - 2 is a correct explanation for Statement - 1.BStatement -1 is True, Statement - 2 is True, Statement -2 is not a correct explanation for Statement - 1.CStatement - 1 is True, Statement - 2 is False.DStatement - 1 is False, Statement - 2 is True.
The resultant of vectors −−→OAand−−→OB is peerpendicular to vec(OA). Find the angle AOB.
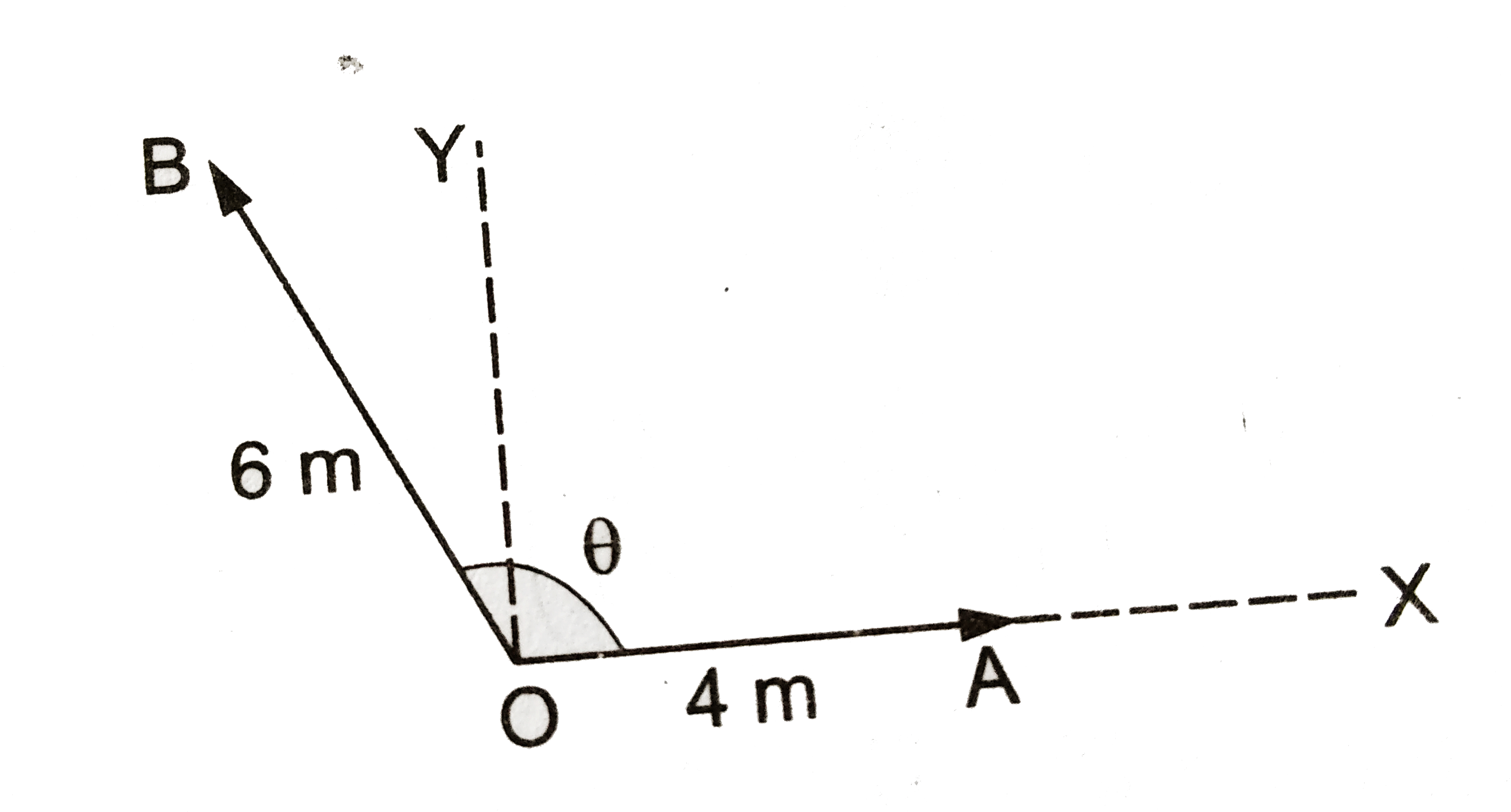 View Solution
View SolutionGiven a parallelogram OACB. The lengths of the vectors −−→OA, −−→OB & −−→AB are a, b & c respectively. The scalar product of the vectors −−→OC & −−→OB is
(A) a2−3b2+c22
(B) 3a2+b2−c22
(C) 3a2−b2+c22
(D) a2+3b2−c22View SolutionFind the resultant of the three vectors →OA,→OB and →OC each of magnitude r as shown in figure?
View SolutionThe sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors −−→OBand−−→OC.
View SolutionIf →a and →b are vectors of equal magnitude, write the value of (→a+→b).→a−→b.
View Solution


