Forces of √2N and 6√2N are acting on a body of mass 10 kg at an angle of 60∘ to each other . Find the acceleration , distance covered and velocity of the body after 10 second , if the body is initially at rest .
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the Resultant Force
We have two forces acting at an angle of 60∘:
- F1=√2N
- F2=6√2N
The formula for the resultant force R when two forces F1 and F2 act at an angle θ is given by:
R=√F21+F22+2F1F2cosθ
Substituting the values:
R=√(√2)2+(6√2)2+2(√2)(6√2)cos(60∘)
=√2+72+2⋅√2⋅6√2⋅12
=√2+72+12
=√86
Step 2: Calculate the Acceleration
Using Newton's second law, F=ma, we can find the acceleration a:
a=Rm
Where m=10kg:
a=√8610
Calculating √86:
√86≈9.27
Thus,
a≈9.2710≈0.927m/s2
Step 3: Calculate the Velocity after 10 seconds
Using the equation of motion:
v=u+at
Where u=0 (initial velocity), a≈0.927m/s2, and t=10s:
v=0+(0.927)(10)≈9.27m/s
Step 4: Calculate the Distance Covered after 10 seconds
Using the equation:
s=ut+12at2
Where u=0:
s=0+12(0.927)(102)
=12(0.927)(100)≈46.35m
Summary of Results
- Acceleration a≈0.927m/s2
- Velocity after 10 seconds v≈9.27m/s
- Distance covered after 10 seconds s≈46.35m
We have two forces acting at an angle of 60∘:
- F1=√2N
- F2=6√2N
R=√F21+F22+2F1F2cosθ
R=√(√2)2+(6√2)2+2(√2)(6√2)cos(60∘)
=√2+72+2⋅√2⋅6√2⋅12
=√2+72+12
=√86
Using Newton's second law, F=ma, we can find the acceleration a:
a=Rm
Where m=10kg:
a=√8610
√86≈9.27
Thus,
a≈9.2710≈0.927m/s2
Using the equation of motion:
v=u+at
Where u=0 (initial velocity), a≈0.927m/s2, and t=10s:
v=0+(0.927)(10)≈9.27m/s
Using the equation:
s=ut+12at2
Where u=0:
s=0+12(0.927)(102)
=12(0.927)(100)≈46.35m
- Acceleration a≈0.927m/s2
- Velocity after 10 seconds v≈9.27m/s
- Distance covered after 10 seconds s≈46.35m
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - conceptual problmes
45 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Very short answer questions
73 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions
17 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
Similar Questions
Forces of 5√2 and 6√2N are acting on a body of mass 1000 kg at an angle of 60∘ to each other. Find the acceleration, distance covered and the velocity of the mass after 10 s.
View SolutionThe force acting on a body of mass 10 kg is (2ˆi+j−ˆk) N. If the body is initially at rest, then velocity at the end of 20 sec will be
View Solution
Knowledge Check
A body of mass 10 kg is acted upon by two forces each of magnitude 10 N making an angle of 60∘ with each other. Find the net acceleration of the body
A2√3ms−2B√3ms−2C3√3ms−2D4√3ms−2Two forces 25 N and 16 N act on a body of mass 1.0 kg. the minimum acceleration will be
A25ms−2B16ms−2C9ms−2D41ms−2A body of mass 2 kg is at rest. Two forces of 6 N and 8 N act on the body at right angles to each other. What is the velocity of the body after 3 second?
A10m/sB15m/sC5m/sD20m/s
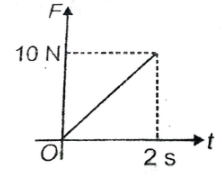
A variable force acts on a body of mass 2 kg initially at rest as shown in figure . Calculate the impulse of the force in first 2 seconds and speed of the body after 2 seconds .
View SolutionTwo forces 25 N and 16 N act on a body of mass 1.0 kg. The minimum acceleration will be
View SolutionTwo forces 25 N and 16 N act on a body of mass 1.0 kg. The minimum acceleration will be
View SolutionFind the acceleration produced by a force of 36 N acting on a body of 6 kg
View SolutionTwo forces 25 n and 16 N act on a body of mass 1.0 kg . The minimum acceleration will be
View Solution