A wooden block of mass 2 kg rests on a soft horizontal floor . When aniron cylinder of mass 25 kg is placed on top of the block , the floor yields steadily , and the block and the cylinder go down with an acceleration of What is the action of the block on the floor (a) before and (b) after the floor yields ? Take . Identify the action reaction pairs in the problem .
To solve the problem, we need to analyze the forces acting on the wooden block before and after the iron cylinder is placed on it.
1. Identify the forces acting on the block:
- The weight of the block (downward force) is given by W=mg, where m=2kg and g=10m/s2.
- The normal force N exerted by the floor on the block acts upward.
2. Calculate the weight of the block:
W=mg=2kg×10m/s2=20N
3. Apply Newton's Third Law:
- According to Newton's Third Law, the action of the block on the floor is equal in magnitude and opposite in direction to the normal force exerted by the floor on the block.
- Therefore, the action of the block on the floor is 20N downward.
(b) Action of the block on the floor after the floor yields:
1. Identify the new system:
- Now, the iron cylinder of mass 25kg is placed on the block, making the total mass M of the system 2kg+25kg=27kg.
2. Calculate the weight of the combined system:
Wtotal=Mg=27kg×10m/s2=270N
3. Apply Newton's Second Law:
- The system is accelerating downward at 0.1m/s2.
- The net force acting on the system can be expressed as:
Wtotal−N=Ma
where a=0.1m/s2.
4. Substituting the known values:
270N−N=27kg×0.1m/s2
270N−N=2.7N
5. Solving for N:
N=270N−2.7N=267.3N
6. Action of the block on the floor:
- Again, by Newton's Third Law, the action of the block on the floor is equal to the normal force exerted by the floor on the block.
- Therefore, the action of the block on the floor after the floor yields is 267.3N downward.
Summary of Results:
- (a) The action of the block on the floor before the floor yields is 20 N.
- (b) The action of the block on the floor after the floor yields is 267.3 N.
Identifying Action-Reaction Pairs:
1. Before the floor yields:
- Action: Block exerts a downward force of 20N on the floor.
- Reaction: The floor exerts an upward normal force of 20N on the block.
2. After the floor yields:
- Action: The block (with the cylinder) exerts a downward force of 267.3N on the floor.
- Reaction: The floor exerts an upward normal force of 267.3N on the block.
- The weight of the block (downward force) is given by W=mg, where m=2kg and g=10m/s2.
- The normal force N exerted by the floor on the block acts upward.
W=mg=2kg×10m/s2=20N
- According to Newton's Third Law, the action of the block on the floor is equal in magnitude and opposite in direction to the normal force exerted by the floor on the block.
- Therefore, the action of the block on the floor is 20N downward.
- Now, the iron cylinder of mass 25kg is placed on the block, making the total mass M of the system 2kg+25kg=27kg.
Wtotal=Mg=27kg×10m/s2=270N
- The system is accelerating downward at 0.1m/s2.
- The net force acting on the system can be expressed as:
Wtotal−N=Ma
where a=0.1m/s2.
270N−N=27kg×0.1m/s2
270N−N=2.7N
N=270N−2.7N=267.3N
- Again, by Newton's Third Law, the action of the block on the floor is equal to the normal force exerted by the floor on the block.
- Therefore, the action of the block on the floor after the floor yields is 267.3N downward.
- (a) The action of the block on the floor before the floor yields is 20 N.
- (b) The action of the block on the floor after the floor yields is 267.3 N.
1. Before the floor yields:
- Action: Block exerts a downward force of 20N on the floor.
- Reaction: The floor exerts an upward normal force of 20N on the block.
- Action: The block (with the cylinder) exerts a downward force of 267.3N on the floor.
- Reaction: The floor exerts an upward normal force of 267.3N on the block.
Similar Questions
A wooden block of mass 1 kg rests on a soft horizontal floor. When an iron cylinder of mass 20kg is placed on top of the block, the floor yields steadily and booth go down with an acceleration of 0.1ms−2. What is the action of the block on the floor (a) before and (b) after the floor yields? (Take g=10ms−2). Identify the action and reaction pairs in the problem.
 View Solution
View SolutionA steel block of 10 kg rests on a horizontal floor as shown. When three iron cylinders are placed on it as shown, the block and cylinders go down with an acceleration 0.2m/s2. The normal reaction R' by the floor if mass of the iron cylinders are equal and of 20 kg each, is ______ N. [Take g=10m/s2andμs=0.2]
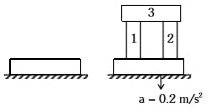 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Block A of mass 35 kg is resting on a frictionless floor.
 A0.8ms−2B2.4ms−2C0.4ms−2D4.4ms−2
A0.8ms−2B2.4ms−2C0.4ms−2D4.4ms−2 - Question 2 - Select One
On the floor of an elevator a block of mass 50 kg is placed on which another block of mass 20 kg is also placed. The elevator is moving up with a constant acceleration 1.5m/s2 Force exerted by 20 kg block on the 50 kg block is nearly:
 A250 NB230 NC170 ND150 N
A250 NB230 NC170 ND150 N - Question 3 - Select One
A block of mass 3kg is placed on a rough horizontal surface (μs=0.4) . A force of 8.7N is applied on the block. The force of friction between the block and floor is .
A8.7NB12NC10NDzero
.A block is kept on the floor of an elevator at rest.The elevator starts descending with an acceleration of 12m/s^(2) .Find the displacement of the block during the first 0*2safter the start.Take g=10m/s^(2)
View SolutionThe elevator shown in fig. is descending with an acceleration of 2ms−2. The mass of the block A=0.5kg. Find the force (in Newton) exerted by block A on block B.
 View Solution
View SolutionA block of mass 2 kg is placed on the floor (μ=0.4). A horizontal force of 7 N is applied on the block. The force of friction between the block & floor is fs. Find the fs.
View SolutionA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-
 View Solution
View SolutionOn the floor of an elevator a block of mass 50 kg is placed on which another block of mass 20 kg is also placed. The elevator is moving up with a constant acceleration 1.5m/s2 Force exerted by 20 kg block on the 50 kg block is nearly:
 View Solution
View Solution

