A bullet of mass 10 gram is fired horizontally into a 5 kg wooden block at rest on a horizontal surface The coefficient of kinetic friction between the block and the surface is 0.1 Calculate the speed of the bullet striking the block if the combination moves 20 m before coming rest .
To solve the problem step by step, we will follow the principles of conservation of momentum and the equations of motion under uniform acceleration.
Step 1: Identify the Given Data
- Mass of the bullet, m1=10grams=0.01kg
- Mass of the block, m2=5kg
- Coefficient of kinetic friction, μk=0.1
- Distance moved before coming to rest, s=20m
Step 2: Conservation of Momentum
When the bullet strikes the block, we can apply the conservation of linear momentum. Before the collision, the block is at rest, and the bullet has an initial velocity u. After the collision, the bullet and block move together with a common velocity v.
The conservation of momentum can be expressed as:
m1u+m2⋅0=(m1+m2)v
This simplifies to:
m1u=(m1+m2)v
From this, we can express v:
v=m1um1+m2
Step 3: Calculate the Deceleration Due to Friction
The frictional force acting on the block and bullet combination is given by:
Ffriction=μk⋅N
where N=(m1+m2)g is the normal force, and g is the acceleration due to gravity (approximately 9.8m/s2). Thus,
N=(0.01+5)⋅9.8=5.01⋅9.8≈49.198N
The frictional force becomes:
Ffriction=0.1⋅49.198≈4.9198N
The deceleration a due to friction is given by:
a=Ffrictionm1+m2=4.91985.01≈0.981m/s2
Step 4: Use the Equation of Motion
We can use the equation of motion to relate the initial velocity v, final velocity (which is 0), acceleration (which is negative due to deceleration), and distance s:
v2=u2+2as
Substituting the known values:
0=v2−2⋅0.981⋅20
This simplifies to:
v2=39.24⟹v=√39.24≈6.26m/s
Step 5: Substitute Back to Find Initial Velocity u
Now we substitute v back into the momentum equation:
v=m1um1+m2
Rearranging gives:
u=v(m1+m2)m1
Substituting the values:
u=6.26⋅(0.01+5)0.01=6.26⋅5.010.01≈313.26m/s
Final Answer
The speed of the bullet striking the block is approximately 313.26m/s.
- Mass of the bullet, m1=10grams=0.01kg
- Mass of the block, m2=5kg
- Coefficient of kinetic friction, μk=0.1
- Distance moved before coming to rest, s=20m
When the bullet strikes the block, we can apply the conservation of linear momentum. Before the collision, the block is at rest, and the bullet has an initial velocity u. After the collision, the bullet and block move together with a common velocity v.
m1u+m2⋅0=(m1+m2)v
This simplifies to:
m1u=(m1+m2)v
From this, we can express v:
v=m1um1+m2
The frictional force acting on the block and bullet combination is given by:
Ffriction=μk⋅N
where N=(m1+m2)g is the normal force, and g is the acceleration due to gravity (approximately 9.8m/s2). Thus,
N=(0.01+5)⋅9.8=5.01⋅9.8≈49.198N
The frictional force becomes:
Ffriction=0.1⋅49.198≈4.9198N
The deceleration a due to friction is given by:
a=Ffrictionm1+m2=4.91985.01≈0.981m/s2
We can use the equation of motion to relate the initial velocity v, final velocity (which is 0), acceleration (which is negative due to deceleration), and distance s:
v2=u2+2as
Substituting the known values:
0=v2−2⋅0.981⋅20
This simplifies to:
v2=39.24⟹v=√39.24≈6.26m/s
Now we substitute v back into the momentum equation:
v=m1um1+m2
Rearranging gives:
u=v(m1+m2)m1
Substituting the values:
u=6.26⋅(0.01+5)0.01=6.26⋅5.010.01≈313.26m/s
The speed of the bullet striking the block is approximately 313.26m/s.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISES40videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Additional Examples / Exercises6videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Short Answer Questions26videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension4videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
Similar Questions
A bullet of mass 0.01 kg is fired horizontal into a 4 kg wooden block block at rest , on a horizontal surface. The coefficient of kinetic friction between the block and surface is 0.25 the combination moves 20 m before coming to rest . With what speed did the bullet strike the block ?
View SolutionA block of mass 1 kg lies on a horizontal surface in a truck. The coefficient of static friction between the block and the surface is 0.6. If the acceleration of the truck is 5m/s2, the frictional force acting on the block is…………newtons.
View Solution
Knowledge Check
- Question 1 - Select One
A block of 5 kg is resting on a horizontal surface. The coefficient of kinetic friction between the block and the surface is 0.2. What is the acceleration with which the block will remove if a force of 9.8 N is applied to it ?
A2m/s2B3m/s2C1.5m/s2D2.5m/s2 - Question 2 - Select One
A bullet of mass 50 g moving horizontally with a velocity 210ms−1 gets embedded in a block of mass 1 kg kept on a rough horizontal surface. If the coefficient of kinetic friction between the block and surface is 0.5. The block- bullet system will move a distance of ______ before coming to res t(Acceleration due to gravity =10ms−2).
A40 mB30 mC20 mD10 m - Question 3 - Select One
A block placed on a rough harizontal surface is imparted a velocity of 10 m/s. the coefficient of kinetic friction between the block and the surface is 0.5 and g=10m/s2. How much distance the block will cover, before coming to rest?
A5 mB7.5 mC12 mD10 m
A 441 gm bullet strikes an d becomes embedded in a 1.54 kg block of wood placed on a horizonatal surface just in front of the gun. If the coefcient of kinetic friction between the block and the surface is 0.28, and the impact drives the block a distance of 18 m before it comes to rest, what was the muzzle speed of the bullet ?
View SolutionWhat is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
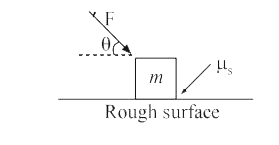 View Solution
View SolutionA block of mass 4 kg is resting on a horizontal table and a force of 10 N is applied on it in the horizontal direction. The coefficient of kinetic friction between the block and the table is 0.1. The work done in √20 s
View SolutionA wooden block of mass M rests on a horizontal surface. A bullet of mass m moving in the horizontal direction strikes and gets embedded in it. The combined system covers a distance x on the surface. If the coefficient of friction between wood and the surface is μ , the speed of the bullet at the time of striking the block is (where m is mass of the bullet)
View SolutionA wooden block of mass M resting on a rough horizontal surface is pulled with a force F at an angle with the horizontal. If is the coefficient of kinetic friction between the block and the surface, then acceleration of the block is -
View Solution

