In the arrangement shown in show that tension in the string between masses m2 and m3 is T=2m1m3gm1+m2+m3
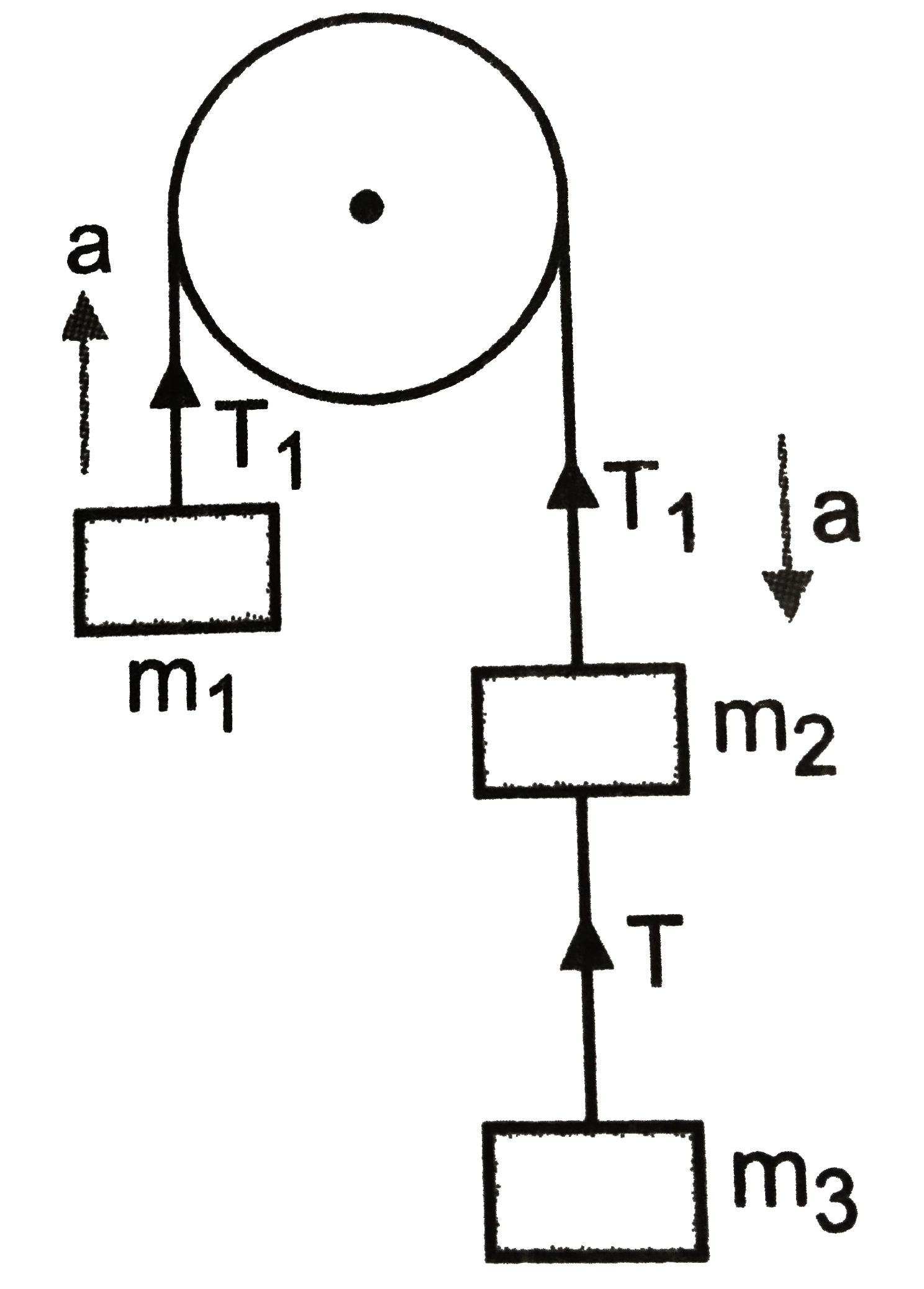
Let T1 be the tension in the string between m1 and
m2 and T be the tension in the string between m2
and m3 If a is acceleration of the system in the
direction shown then
m1a=T1−m1g ….(i)
(m2+m3)a=(m2+m3)g−T1 ....(ii)
and m3a=m3g−T ...(iii)
Adding (i) and(ii) (m1+m2+m3a=(m2+m3−m1)g
a=(m2+m3−m1)g/(m1+m2+m3)
put in (iii) m3(m2+m3−m1)gm1+m2+m3=m3g−T
T=m3g−m3(m2+m3−m1)gm1+m2+m3
T=2m1m3g/(m1+m2+m3) .
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - JEE (Main and Advanced)/ Medical Entrance Special
93 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Integer Type Questions
7 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Fill in the blanks
20 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
Similar Questions
Three blocks arranged with pullwy and spring as shown in fig. If the string connecting blocks m2 and m3 is cut at point A, find the acceleration of masses m1,m2 and m3. Just after the string is cut at point A.
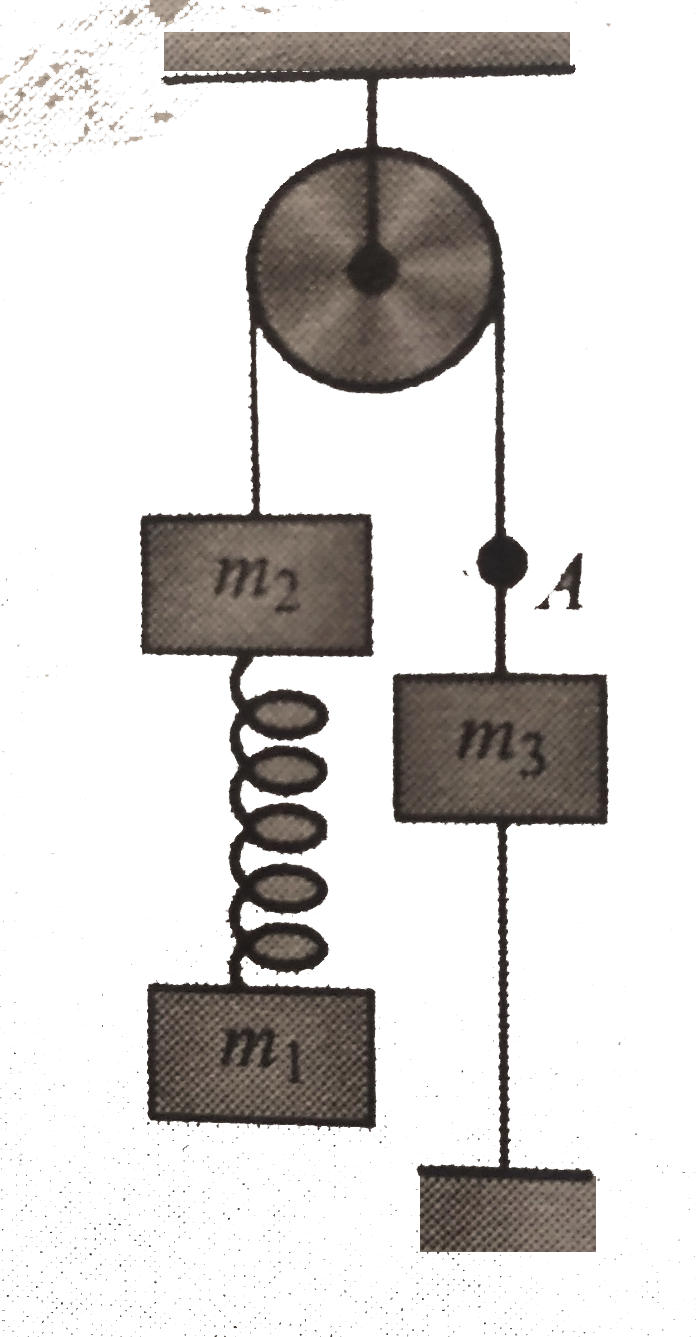
View SolutionThree blocks arranged with pullwy and spring as shown in fig. If the string connecting blocks m2 and m3 is cut at point A, find the acceleration of masses m1,m2 and m3. Just after the string is cut at point A.

View Solution
Knowledge Check
In the arrangement shown in the all contact surfaces are smooth strings and pulleys are massless
Given M1=1kg,M2=2kg,M3=4kg and g=10ms−2
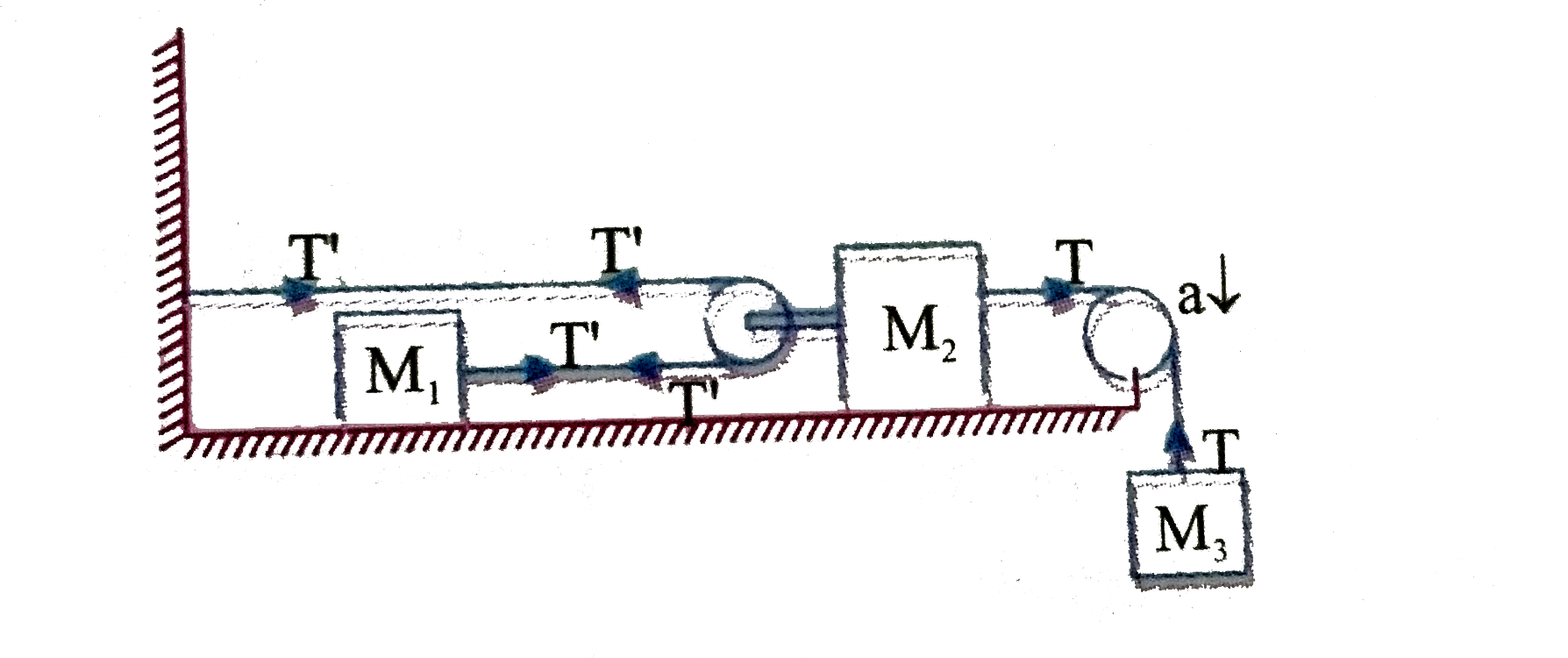 .AThe acceleration of block of mass M3 is 4ms−2BThe acceleration of block of mass M1 is 4ms−2CThe tension (T) in the string connecting blocks of masses M3 and M2 is 24N .DThe tension (T) in the string connecting blocks of masses M1 and M2 is 24N .
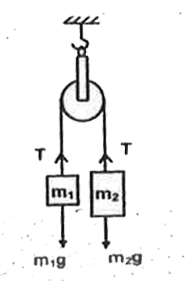
.AThe acceleration of block of mass M3 is 4ms−2BThe acceleration of block of mass M1 is 4ms−2CThe tension (T) in the string connecting blocks of masses M3 and M2 is 24N .DThe tension (T) in the string connecting blocks of masses M1 and M2 is 24N .Consider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
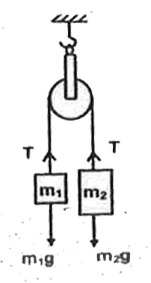
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?A75NB150NC300ND500NConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
What is the tension in the string?A60NB75NC100ND600N
The tension in the string connected between blocks is

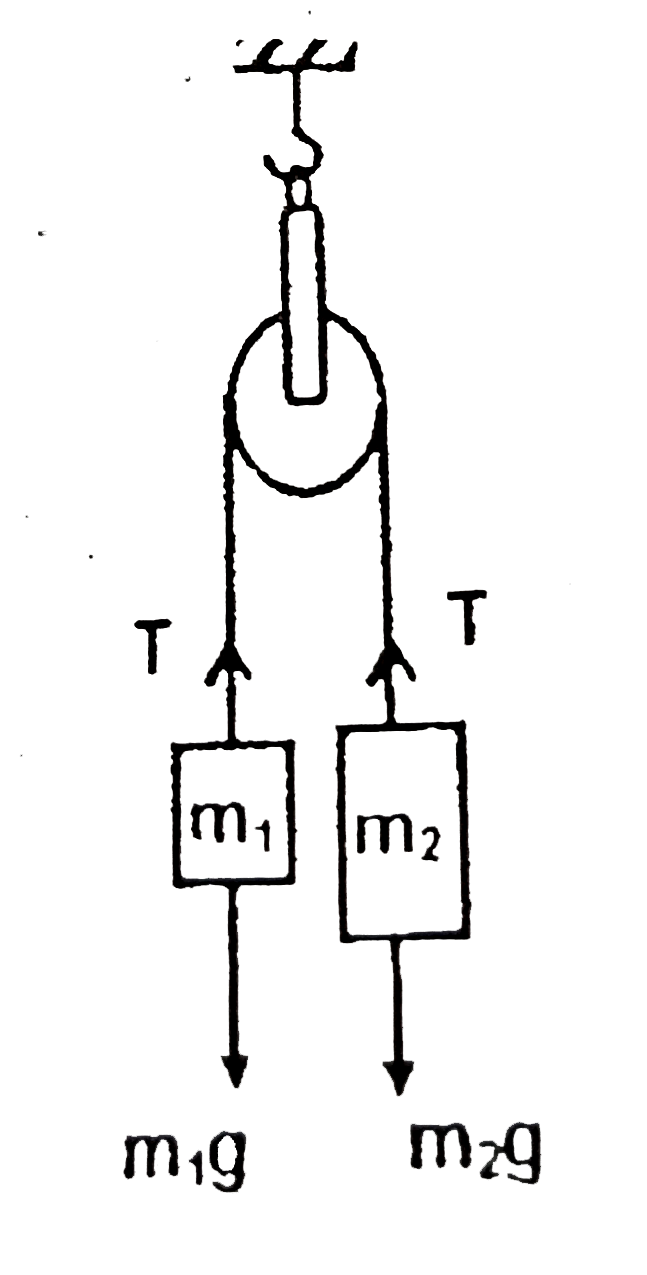
View SolutionConsider the case of two bodies of masses m1 and m2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations :
(i) when m1>m2. In this case
a=(m1−m2m1+m2)g and T=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)g and T=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0, T=mg
If m1=10kg, m2=6kg and g=10m/s2
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string
View SolutionFigure shows two shells of masses m1 and m2 . The shells are concentric. At which point, a particle of mass m shall experience zero force?
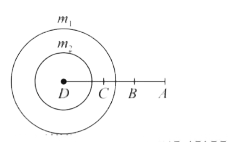
View SolutionFigure shows two shells of masses m1 and m2 . The shells are concentric. At which point, a particle of mass m shall experience zero force?
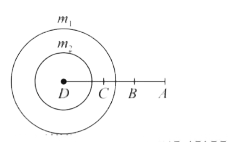
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
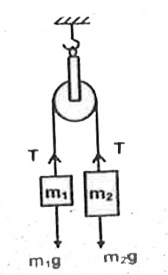
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
If m1=10kg,m2=6kgandg=10m/s2 then what is the acceleration of masses?
View Solution
