A point particle of mass m, moves long the uniformly rough track PQR as shown in figure. The coefficient of friction, between the particle and the rough track equals μ. The particle is released, from rest from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR.
The value of the coefficient of friction μ and the distance x (=QR), are, respectively close to:

0.2 and 6.5m
0.2 and 3.5m
0.29 and 3.5m
0.29 and 6.5m
The correct Answer is:C
As energy lost over PQ= energy lost over QR
∴(μmgcosθ)PQ=(μmg)QR
or QR=PQcosθ .....(i)
From figure, sinθ=sin30∘=2PQ=12
PQ=4m
From (i), QR=4cos30∘=4√32=2√3m=3.5m
Again, decrease in P.E.= loss of energy due to friction in PQ and QR
mgh=(μmgcosθ)PQ+μmg×QR
h=μcosθ×PQ+μmg×QR
h=μcosθ×PQ+μ×QR
2=μcos30∘×4+μ×2√3
=μ(4×√32+2√3)=μ×4√3
μ=24√3=12√3=0.29
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Comprehension
9 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Integer Type Questions
9 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - NCERT( Multiple choide questions-1)
21 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
A small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
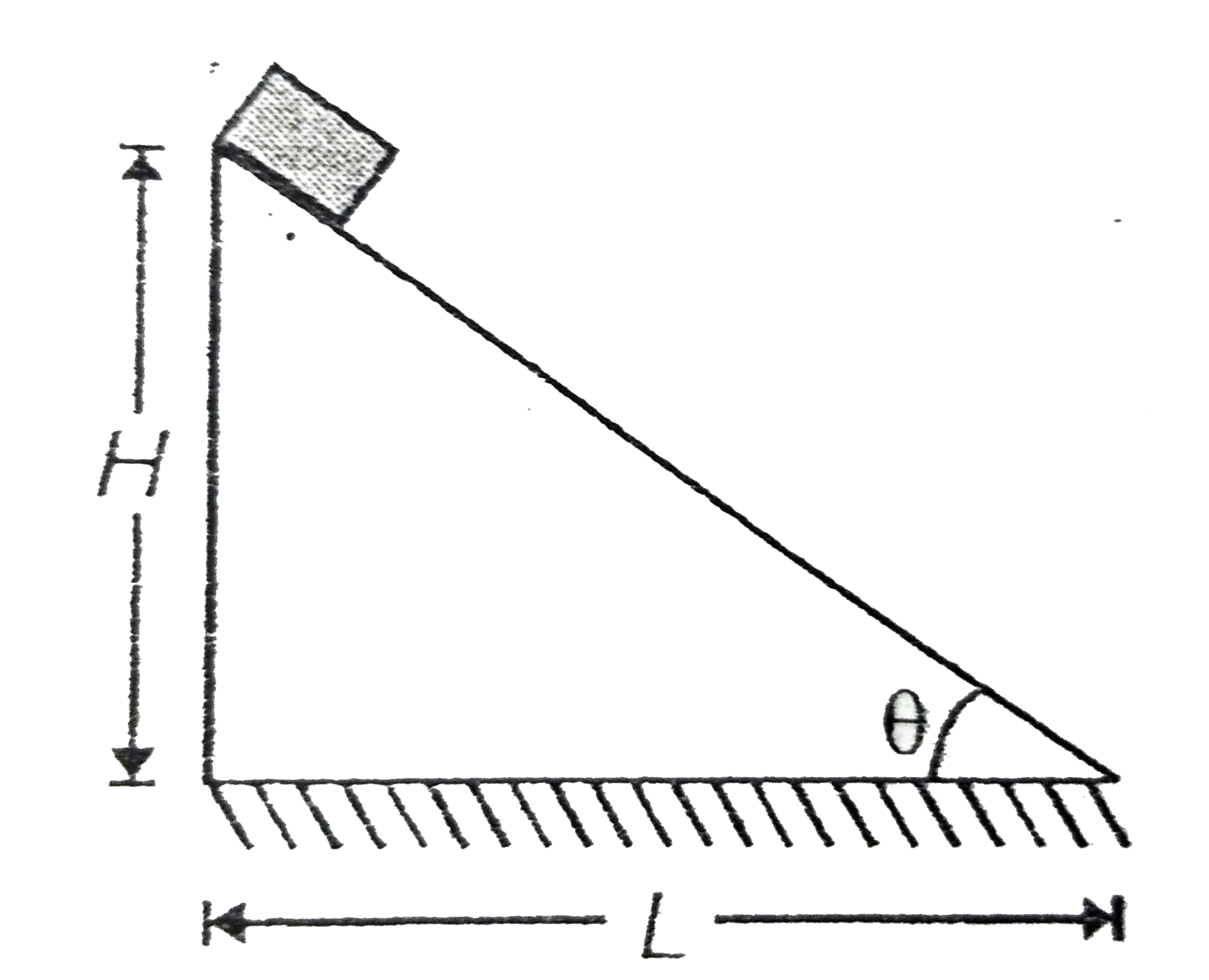
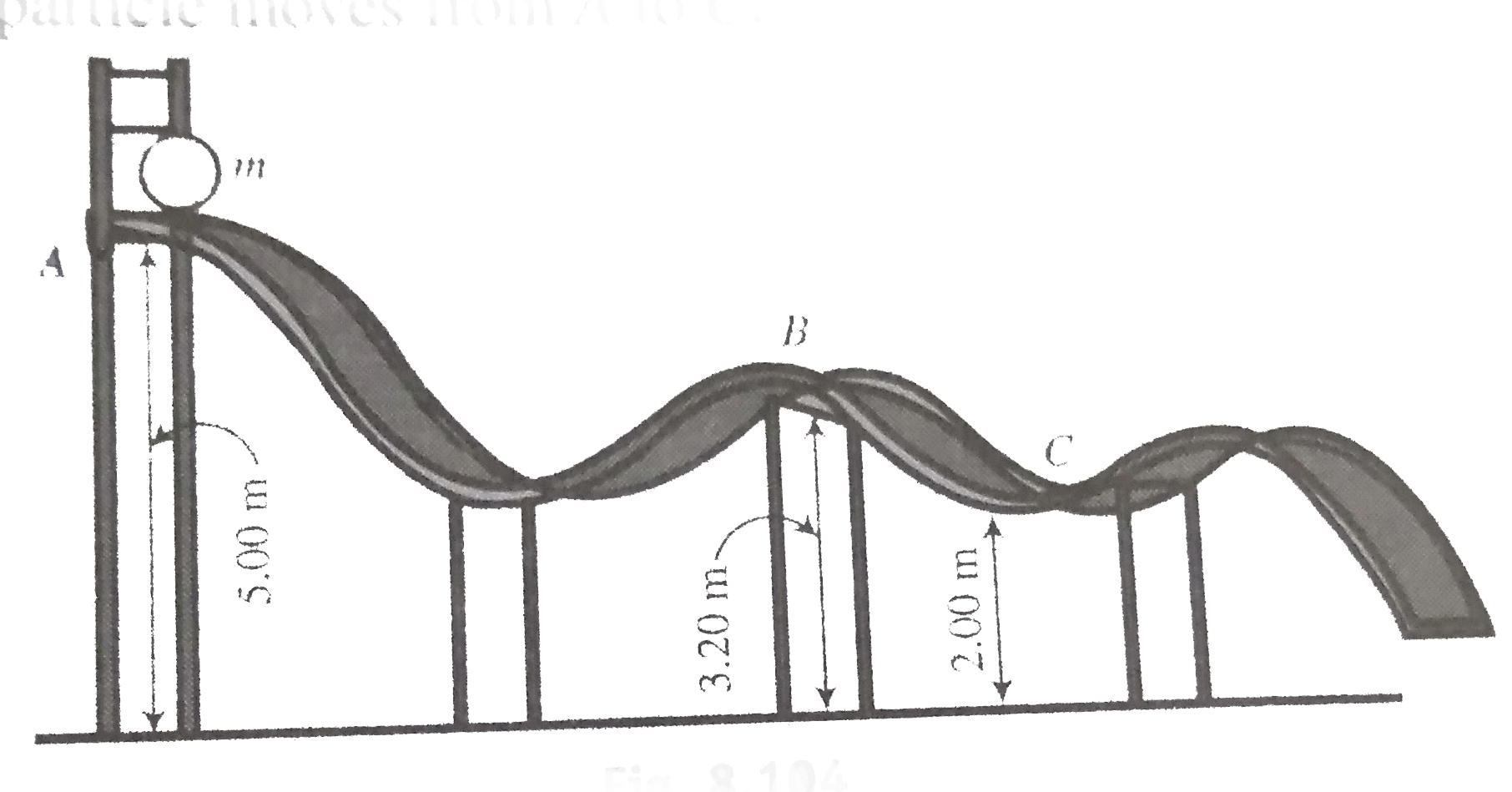
View SolutionA particle of mass m=5.00kg is released from point A and it slides on the frictionless track shown in figure. Determine (a) the particle's speed at points B and C and (b) the net work done by the gravitational force as the particle moves from A to C.
View Solution
Knowledge Check
A particle of mass m is released from rest and follows a particle as a function of time?
 A
A B
B C
C D
D
Figure shows an irregular wedge of mass m placed on a smooth horizontal surface. Part BC is rough.
If the coefficient of friction between the block and wedge is μ, and the block comes to rest with respect to wedge at a point E on the rough surface then BE will beAHμBH−hμChμDnone of theseA particle of mass m slides along a curved-flat-curved track. The curved portions of the track are smooth. If the particle is released at the top of one of the curved portions, the particle comes to rest at flat portion of length l and of μ=μkinetic after covering a distance of
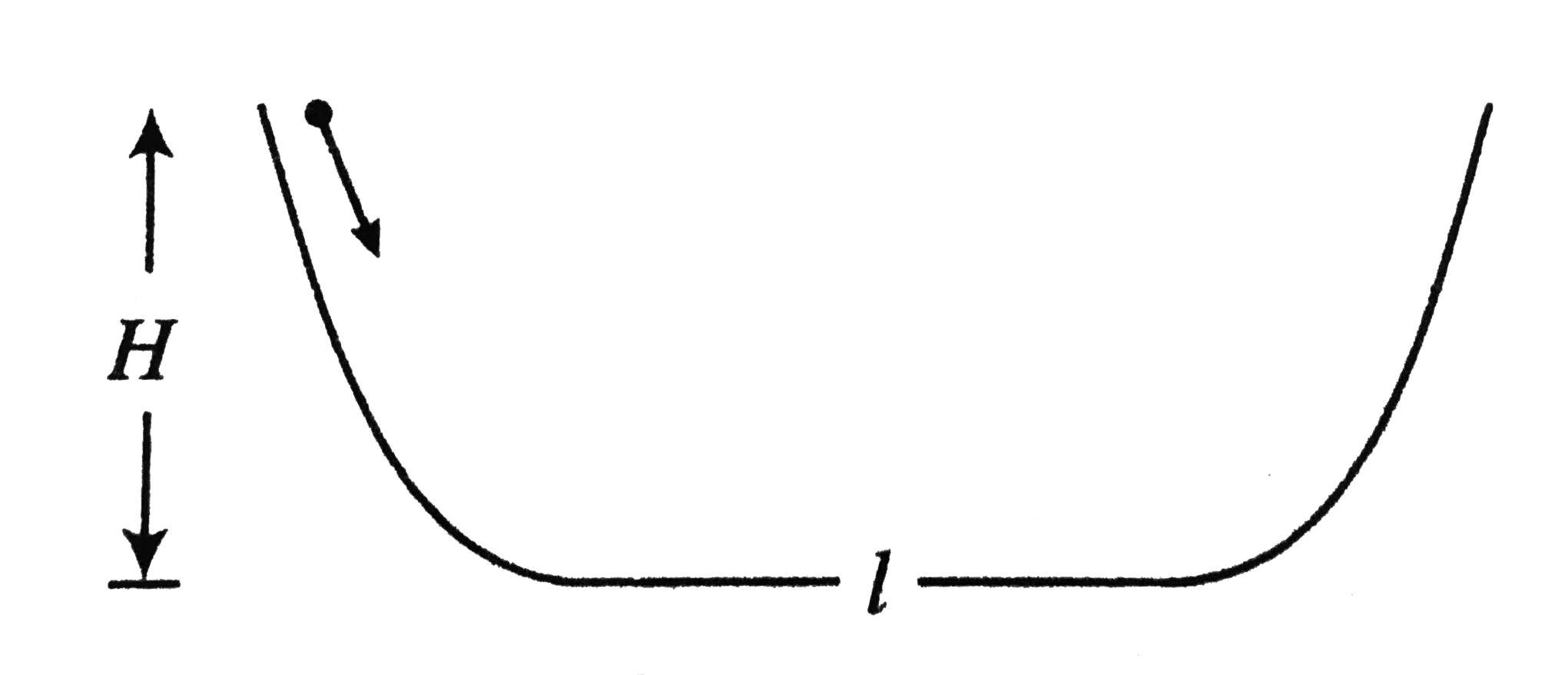 A(a) l3μB(b) H2μkineticC(c) l6D(d) Hμkinetic
A(a) l3μB(b) H2μkineticC(c) l6D(d) Hμkinetic
A point particle of mass m is released from a distance √3R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.

View SolutionA block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
View SolutionA small roller coaster starts at point A with a speed u on a curved track as shown in the figure
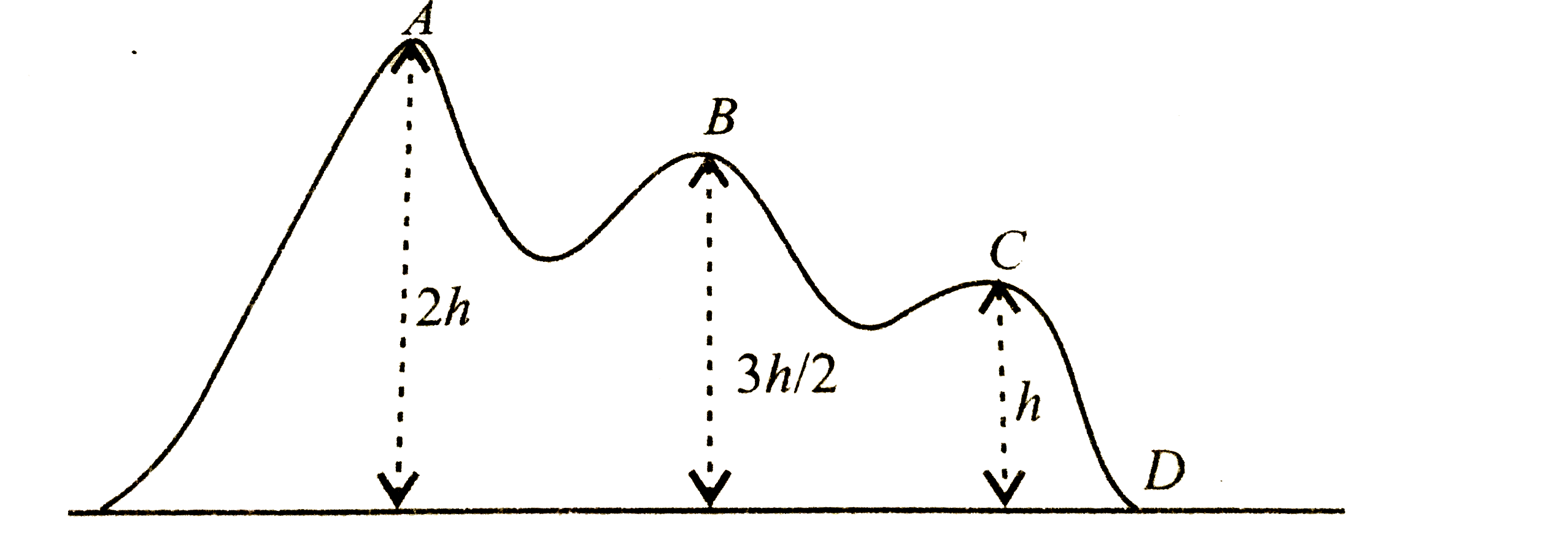
The friction between the roller coaster and the track is negligible and it always remains in contact with the track. The speed of roller coaster at point D on the track will be
View SolutionA particle initially at rest is released from A as shown in figures. The approximate variation of direction of resultant acceleration as particle moves from A to B is :

View SolutionA particle moves in one dimension in a conservation force field. The potential energy is depicted in the graph below.
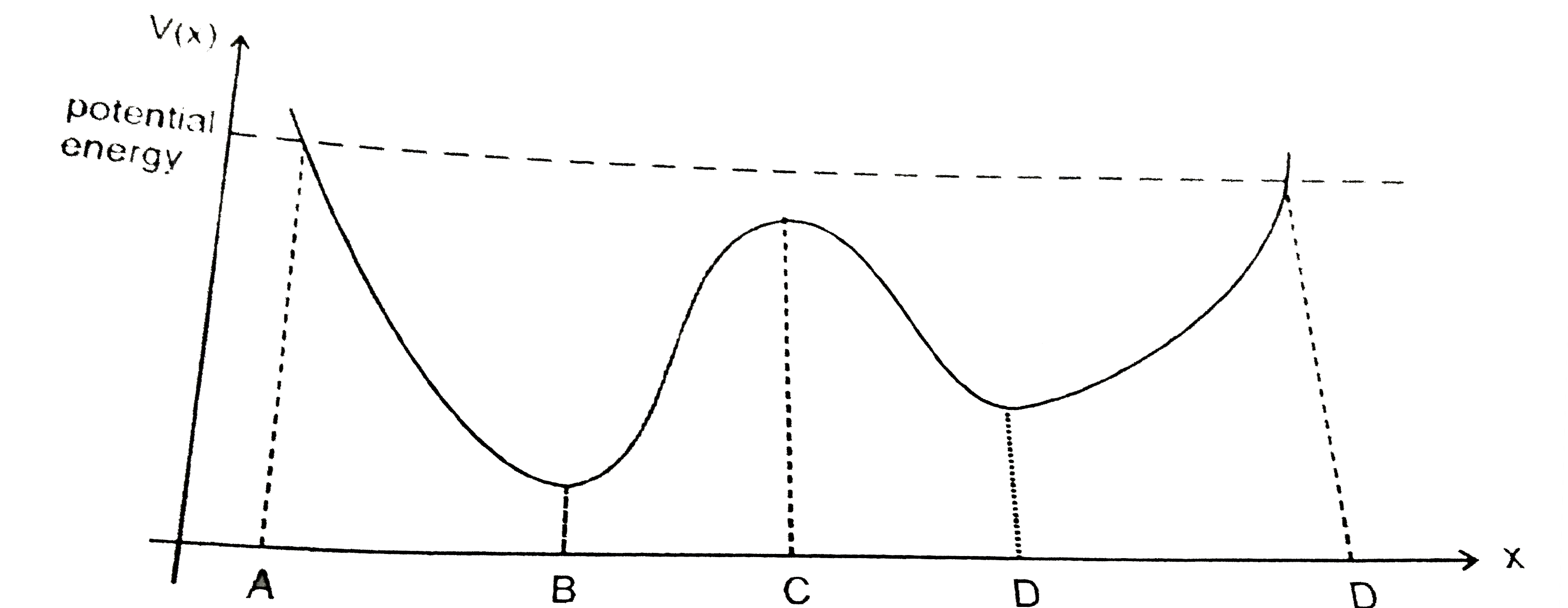
If the particle starts to move from rest from the point A, then
View Solution
