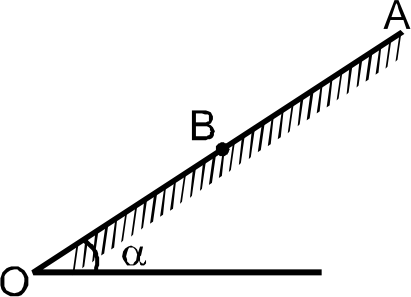
O is a point at the bottom of a rough plane inclined at an angle α to the horizontal. Coefficient of friction
between AB is
Tanα2
and between BO is 3Tanα2
. B is the mid–point of AO. A block is released from rest at A. Then identify which graphs are correct during motion of block from point A to O taking direction down the incline plane as positive (sinα=1/5) :
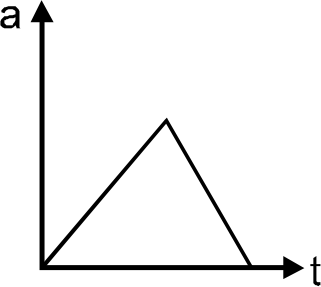
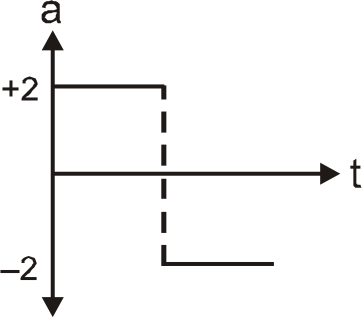
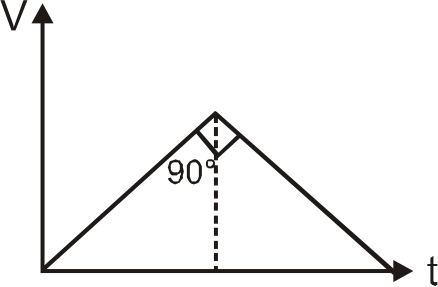
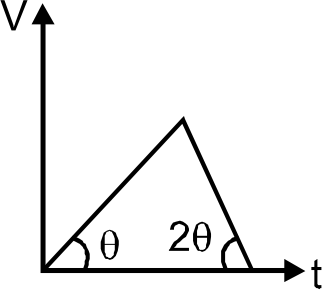
The correct Answer is:C
For motion between AB
ma=mgsinα−tanα2mgcosα
a=gsinα2 (downward)
For motion between BO
ma=3tanα2mgcosα−mgsinα
a=gsinα2 (upward)
The velocity increases from zero to maximum value of B and then starts decreasing with same rate and finally becomes zero at O.
Topper's Solved these Questions
Similar Questions
A block rests on a rough inclined plane making an angle of 30° with the horizontal. The coefficient of static friction between the block and inclined plane is 0.8. If the frictional force on the block is 10 N, the mass of the block is
View SolutionA block is at rest at the top of a rough inclined plane of inclination 30° with the horizontal. What is the coefficient of kinetic friction between the block and the plane, if the . block slides down with an acceleration of g5 ?
View Solution
Knowledge Check
O is a point at the bottom of a rough plane inclined at an angle α to horizontal Coefficient of friciton between AB is tanα2 and between BO is 3tanα2B is the middle point of AO, A block if released from rest at A, then which of the following graphs are correct :
 A
A B
B C
C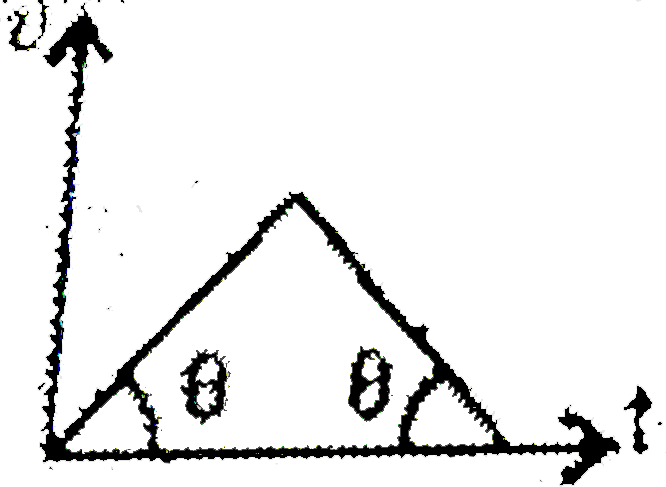 D
D
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A9.8NB0.7×9.8×√3NC9.8×√3ND0.7×9.8NA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
Amg cos θBmgCmg sin θDNone of these
A block rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.8. If the frictional force on the block is 10N, the mass of the block (in kg) is
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
View SolutionA block is lying on an inclined plane which makes 60∘ with the horizontal. If coefficient of friction between block and plane is 0.25 and g=10m/s2, , then acceleration of the block when it moves along the plane will be
View SolutionA block rests on a rought inclined plane making an angle of 30∘ with horizontal. The coefficient of static friction between the block and inclined plane is 0.8 . If the frictional foerce on the block is 10N, the mass of the block in kg is (g=10m/s2)
View Solution
