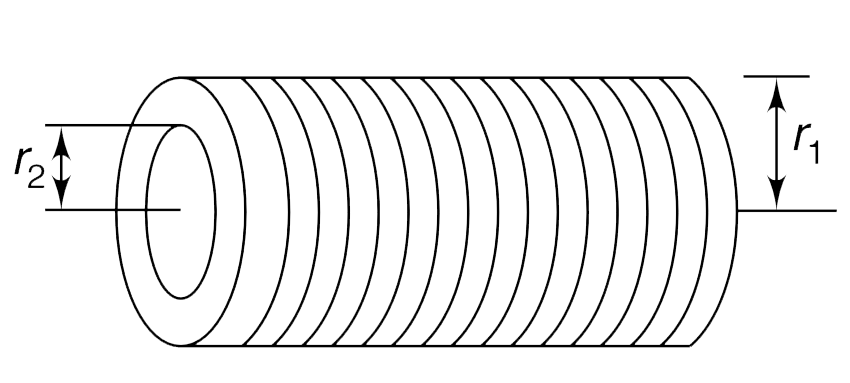
Two coaxial long solenoids of equal length have current, i1,i2, number of turns per unit length n1,n2 and radius r1,r2 respectively. If n1i1=n2i2 and the two solenoids carry current in opposite sence, the magnetic energy stored per until length is [r2>r1]
μ02n21π(r22−r21)
μ0n21i21π(r22r21)
μ02n21i21πr21
μ02n22i22πr22
Magnetic field is non zero only in the region between the two solenoids, where B=μ0n2i2
∴ energy stored per unit volume =B22μ0=μ0n22i222
The energy per unit length.=energy per unit volume x area of cross section where B≠0
=μ0n22i222[π(r22−r21)]=μ0n21i212[π(r22−r21)] , since nii1−n2i2
Topper's Solved these Questions
Similar Questions
Two long co-axial solenoids have radii, and number of turns per unit length equal to r1,r2 and n1,n2 respectively where suffix 1 refers to the outer solenoid and 2 refers to the inner solenoid. Length of both is l. The current in the outer solenoid is made to grow as I1=kt where t is time. Resistance of the wire used in inner solenoid is R. Write the current induced in the inner solenoid assuming that it is shorted.
 View Solution
View SolutionThere are two long co-axial solenoids of same length l. The inner and other coils have redii r1 and r2 and number of turns per unti length n1 and n2 respectively .The reatio of mutual inductance to the self - inductance of the inner- coil is :
View Solution
Knowledge Check
- Question 1 - Select One
A long solenoid with 40 turns per cm carries a current of 1 A. The magnetic energy stored per unit volume is..... J m−3.
A3.2πB32πC1.6πD6.4π - Question 2 - Select One
Two coaxil solenoids 1 and 2 of the same length are set so that one is inside the other. The number of turns per unit length are n1 and n2. The current i1 and i2 are flowing in opposite directions. The magnetic field inside the inner coil is zero. This is possible when
Ai_(2)cancel(=)i_(2) and n1=n2Bi2=i2 and n_(1)cancel(=)n_(2)Ci2=i2 and n1=n2Di1n1=i2n2 - Question 3 - Select One
Magnetic field of a straight solenoid carrying carried 1 and having a n turns per unit length given by:
AB=μ0nI2BB=μ0nICB=μ0n2IDμ0n2I4
Find the mutual inductance of two long concentric solenoids for a length I. The area of cross-section of inner solenoid is A and number of turns per unit length are n1 and n2.
View SolutionTwo coaxial solenoids having same number of turns per unit length n, and radius R and 2R respectively have no current initially. Current in both grows uniformly such that current in the inner one is twice that of the outer one, at any instant of time in the same direction. Current in outer one at time t is Kt then induced electric field at a distance r from axis is (R<r<2R).
View SolutionIn a solenoid, the corrent flowing through the wire is I and number of turns per unit length is n. This gives a magnetic field B inside the solenoid. If number of turn per unit length is increased to 2n, what will be the value of magnetic field in the solenoidgt
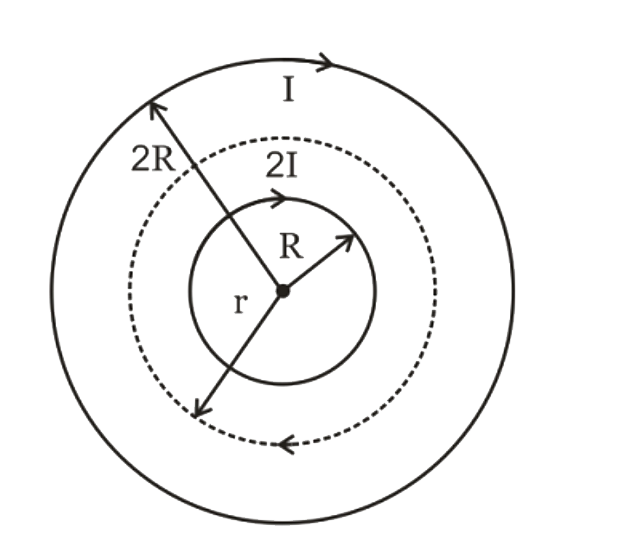
View SolutionTwo long coaxial solenoids of radius R and 2R have equal number of turns per unit length. They carry time-varying currents. i1=2ktandi2=kt respectively, in the same direction. A point charge released between the solenoids at a distance r, is seen to move along a circular path. Then the value of r is
 View Solution
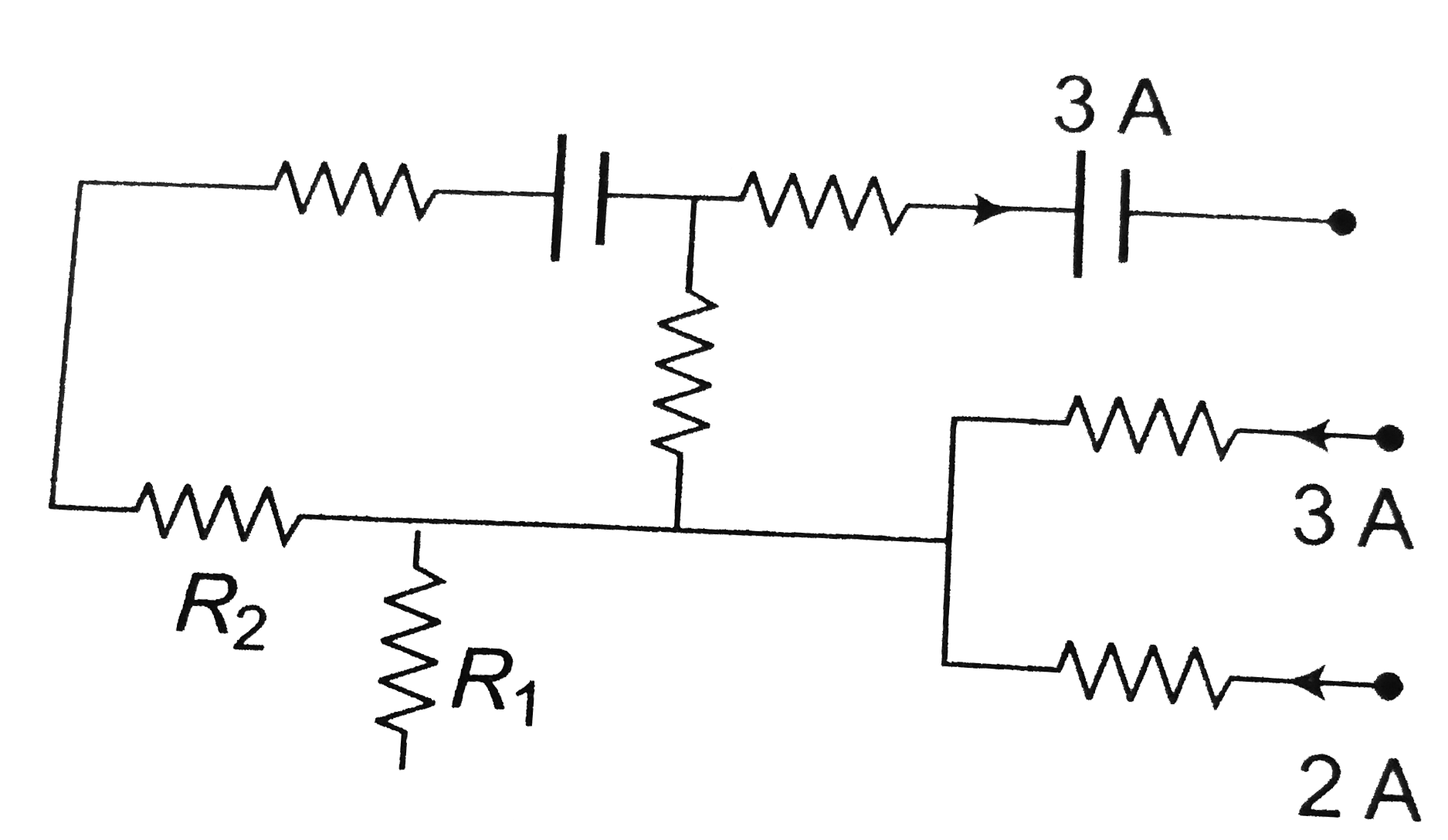
View SolutionIn the given circuit if I1 and I2 be the current in resistance R1 and R2 respectively then:
 View Solution
View Solution

