Two coaxial solenoids having same number of turns per unit length n, and radius R and 2R respectively have no current initially. Current in both grows uniformly such that current in the inner one is twice that of the outer one, at any instant of time in the same direction. Current in outer one at time t is Kt then induced electric field at a distance r from axis is (R<r<2R).
Not possible
μ0nK2r(2R2+r2)
2μ0nKR2r
2μ0nKr(2R2−r2)
The correct Answer is:B
To solve the problem, we need to determine the induced electric field at a distance r from the axis of two coaxial solenoids. Here's a step-by-step solution:
Step 1: Define the currents in the solenoids
Let the current in the outer solenoid be Iouter=Kt. Since the current in the inner solenoid is twice that of the outer one, we have:
Iinner=2Iouter=2Kt
Step 2: Determine the magnetic field produced by each solenoid
The magnetic field B inside a solenoid is given by:
B=μ0nI
where μ0 is the permeability of free space, n is the number of turns per unit length, and I is the current.
For the inner solenoid:
Binner=μ0n(2Kt)=2μ0nKt
For the outer solenoid:
Bouter=μ0n(Kt)=μ0nKt
Step 3: Calculate the total magnetic field at a distance r (where R<r<2R)
In the region between the two solenoids (i.e., R<r<2R), the magnetic field due to the inner solenoid will dominate since the outer solenoid's field is zero in that region. Thus, the total magnetic field B at distance r is:
B=Binner=2μ0nKt
Step 4: Calculate the magnetic flux through a circular loop of radius r
The magnetic flux Φ through a circular loop of radius r is given by:
Φ=B⋅A=B⋅πr2
Substituting for B:
Φ=(2μ0nKt)⋅πr2=2μ0nKtπr2
Step 5: Determine the induced electric field using Faraday's Law
According to Faraday's Law of electromagnetic induction, the induced electromotive force (emf) is equal to the negative rate of change of magnetic flux:
E=−dΦdt
Calculating the derivative:
dΦdt=2μ0nKπr2
Thus, the induced emf is:
E=−2μ0nKπr2
Step 6: Relate the induced emf to the electric field
The induced emf around a circular path of radius r is also given by:
E=E⋅2πr
Setting the two expressions for emf equal gives:
E⋅2πr=−2μ0nKπr2
Solving for E:
E=−2μ0nKπr22πr=−μ0nKr1
Thus, the induced electric field at a distance r from the axis is:
E=−μ0nKr1
Final Answer
The induced electric field at a distance r from the axis, where R<r<2R, is:
E=−μ0nKr1
Let the current in the outer solenoid be Iouter=Kt. Since the current in the inner solenoid is twice that of the outer one, we have:
Iinner=2Iouter=2Kt
The magnetic field B inside a solenoid is given by:
B=μ0nI
where μ0 is the permeability of free space, n is the number of turns per unit length, and I is the current.
Binner=μ0n(2Kt)=2μ0nKt
Bouter=μ0n(Kt)=μ0nKt
In the region between the two solenoids (i.e., R<r<2R), the magnetic field due to the inner solenoid will dominate since the outer solenoid's field is zero in that region. Thus, the total magnetic field B at distance r is:
B=Binner=2μ0nKt
The magnetic flux Φ through a circular loop of radius r is given by:
Φ=B⋅A=B⋅πr2
Substituting for B:
Φ=(2μ0nKt)⋅πr2=2μ0nKtπr2
According to Faraday's Law of electromagnetic induction, the induced electromotive force (emf) is equal to the negative rate of change of magnetic flux:
E=−dΦdt
Calculating the derivative:
dΦdt=2μ0nKπr2
Thus, the induced emf is:
E=−2μ0nKπr2
The induced emf around a circular path of radius r is also given by:
E=E⋅2πr
Setting the two expressions for emf equal gives:
E⋅2πr=−2μ0nKπr2
Solving for E:
E=−2μ0nKπr22πr=−μ0nKr1
Thus, the induced electric field at a distance r from the axis is:
E=−μ0nKr1
The induced electric field at a distance r from the axis, where R<r<2R, is:
E=−μ0nKr1
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Similar Questions
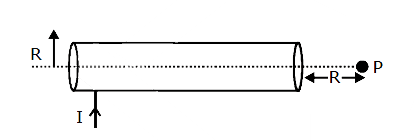
An infinite long solenoid having n turns per unit length is shown in figure. The magnetic field at P, when a current I is flowing through it would be
 View Solution
View SolutionA long solenoid of radius 2R contains another coaxial solenoid of radius R. The coils have the same number of turns per unit length and initially both carry zero current. At time, t=0, current start increasing linearly with time in both solenoids. At any moment the current flowing in the inner coil is twice as large as that in the outer one and their directions are same. A charged particle, initially at rest between the two solenoids, start moving along a circular trajectory due to increasing current in the solenoid as shown in the figure What is the radius of the circle ? (Assume magnetic field due to each solenoid remains uniform over its cross-section.)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The magnetic field on the axis of a long solenoid having n turns per unit length and carrying a current is
Aμ0niBμ0n2iCμ0ni2Dnone of these - Question 2 - Select One
The current flowing in two coaxial coils in the same direction. On increasing the distance the two, the electric current will
AincreaseBdecreaseCremain unchangedDthe information is incomplete - Question 3 - Select One
The magnetic field B within the solenoid having n turns per unit length and carrying a current I is given by
Aμ0nIB4πμ0nICnIDμ0nIl
A long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
View SolutionA current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor of the cable, then the magnetic induction at any point outside the conductor at a distance r meter from the axis is
View SolutionA solenoid of radius R and length L has a current I=I0 cosωt. The value of induced electric field at a distance of r outside the solenoid, is
View SolutionA long solenoid of radous R has n turns of wire per unit length and carries a time-varying current that varies sinusiodally as I=Imaxcosωt, where Imax is the maximum current and ω I the angular frequancy of the alternating current source (shows in Fig.)

The magnitude of the induced electric field inside tha solenoid, a distance r<R from its long central axis isView SolutionThe hollow cylinder of length l and inner and outer radius R1 and R2 respectively. Find resistance of cylinder if current flows radially outward in the cylinder. Resistivity of material of cylinder id ρ .
View Solution

