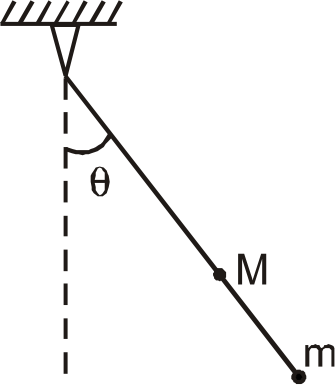
A massless stick of length L is hinged at one end and a mass m attached to its other end. The stick is free to rotate in vertical plane about a fixed horizontal axis passing through frictionless hinge. The stick is held in a horizontal position. At what distance x from the hinge should a second mass M = m be attached to the stick, so that stick falls as fast as possible when released from rest

√2L
√3L
(√2−1)L
(√3−1)L
Angular acceleration or rod
α=m(x+L)gsinθm(x2+L2)
For rod to fall as fast as possible, dαdx=0
or x=(√2−1)L
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
17:56View SolutionWhen p−n junction diode is forward biased then
05:28View SolutionA metre stick weighing 240 g is pivoted at its upper end in such a way that it can freely rotate in a vertical plane through this end figure. A particle of mass 100 g is attached to the upper end of the stick through a light sting of length 1 m. Initially the rod is kept veritcal and the string horizontal when the system is released from rest. The particle colides with the lower end of the stick and sticks there. Find the maximum angle through which the stick will rise.
 03:17View Solution
03:17View SolutionA rod of uniform cross-section of mass M and length L is hinged about an end to swing freely in a vertical plane. Howerver, its density is non uniform and varies linearly from hinged end to the free end doubling its value. The moment of inertia of the rod, about the rotation axis passing through the hinge point
02:10View SolutionA uniform stick of length l is hinged so as to rotated about a harmonic axis perpendicular to the stick, at a distance from the center . Find the value of x, for which the time period is minimum.
View SolutionA uniform stick of mass M is placed in a frictionless well as shown. The stick makes an angle θ with the horizontal. Then the force which the vertical wall exerts on right end of stick is :
 02:24View Solution
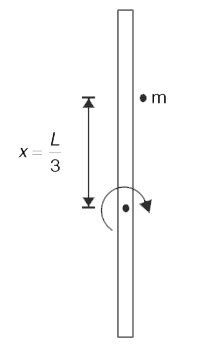
02:24View SolutionA uniform thin stick of mass M=24kg and length L rotates on a friction less horizontal plane, with its centre of mass stationary. A particle of mass m is placed on the plane at a distance x=L3 from the centre of the stick . This stick hits the particle elastically
(a) Find the value of m so that after the collision, there is no rotational motion of the stick
(b) For what minimum of x can we get a value of ‘m’ so that the rod has no rotational motion after elastic collision ?
 01:48View Solution
01:48View SolutionA uniform stick of mass m and length l with I=1/12 ml^(2) spins around on a frictionless horizontal plane, with its CM stationary A mass M is placed on the plane, and the stick collides elastically with it, as shown (with the contact point being the end of the stick) What should be the ratio of m//M be so that after the collision the stick has translational motion but no rotational motion?
02:47View SolutionA uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity ω about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
01:50View SolutionA uniform stick of mass M and length L is kept vertical on a frictionless horizontal floor. If the stick is allowed to fall, then mark the correct alternatives
02:39View SolutionThe M.I. of a thin uniform stick of mass 9 gm about an axis passing through one end perpendicular to the length of a meter stick is
04:06View SolutionA uniform rod of mass m and length / is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity vo collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
02:12View SolutionA rod of uniform cross-section of mass M and length L is hinged about an end to swing freely in a vertical plane. Howerver, its density is non uniform and varies linearly from hinged end to the free end doubling its value. The moment of inertia of the rod, about the rotation axis passing through the hinge point
03:54View SolutionA uniform stick of length l and mass m lies on a smooth table. It rotates with angular velocity ω about an axis perpendicular to the table and through one end of the stick. The angular momentum of the stick about the end is
04:19View SolutionA uniform stick of length l is hinged so as to rotated about a harmonic axis perpendicular to the stick, at a distance from the center . Find the value of x, for which the time period is minimum.
05:03View Solution

