A small block is kept on a platform executing SHM in the horizontal plane, described by x=Asinωt. The time period of SHM is T and the coefficient of friction between the block and the platform is μ. The condition that the block does not slip on the platform at any instant is μ≥xπ2AgT2 then write the value of 'x'

N=Mg
f=ma
As f must be static friction (No slip condition)
f≤μN⇒ma≤μmg
or ma0≤μmg
∴mAω2≤μmg
∴Ω≤√μgA
ω=2πT≤√μgA
∴T≥2π√Aμg⇒μ≥4π2AgT2
Topper's Solved these Questions
Similar Questions
A block is kept on a horizontal table that is executing simple harmonic motion of frequency v in the horizontal plane. The coefficient of static friction between the block and the table is μ. Determine the maximum amplitude of the table for which the block does not slip on the surface of the table.
View SolutionA block of mass m is kept on horizontal turn table at x distance from the centre. If coefficient of friction between block and surface of turn table is μ, then maximum angular speed of the table so that block does not slip
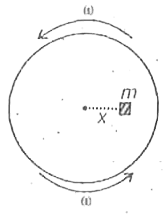
View Solution
Knowledge Check
A block is resting on a horizontal plate in the xy plane and the coefficient of friction between block and plate is μ. The plate begins to move with velocity v=bt2 in x direction At what time will the block start sliding on the plate?
AμbgBμbg2CμgbDμg2bA block is kept on a rough horizontal plank. The coefficient of friction between the block and the plank is 12. The plank is undergoing SHM of angular frequency 10 rad/s. The maximum amplitude of plank in which the block does not slip over the plank is (g= 10 m/s2)
A4cmB5cmC10 cmD16 cmA cart of mass M has a block of mass m in contact with it as shown in the figure-2.133. The coefficient of friction between the block and the cart is μ. What is the minimum acceleration of the cart so that the block m does not fall ?
 AμgBg/μCμ/gDMμg/m
AμgBg/μCμ/gDMμg/m
A rod AB of length 2m is hinging at point A and its other end B is attached to a platform on which a point of mass m is kept. Rod rotates about point A maintain angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path. If the coefficient of static friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the platform (g=10ms−2)
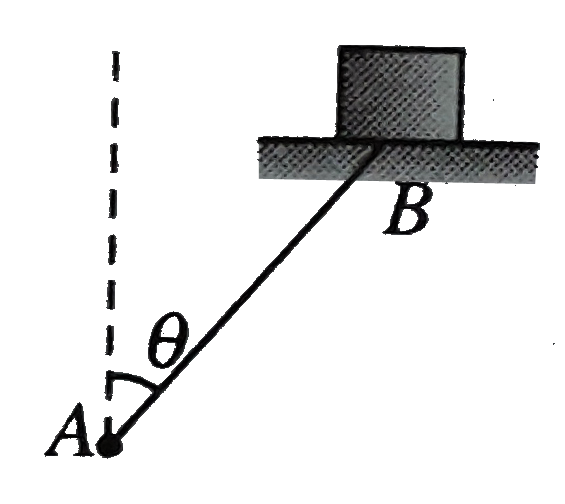
View SolutionTwo block of masses m1 and m2 are connected with a massless unstretched spring and placed over a plank moving with an acceleration 'a' as shown in figure. The coefficient of friction between the blocks and platform is μ
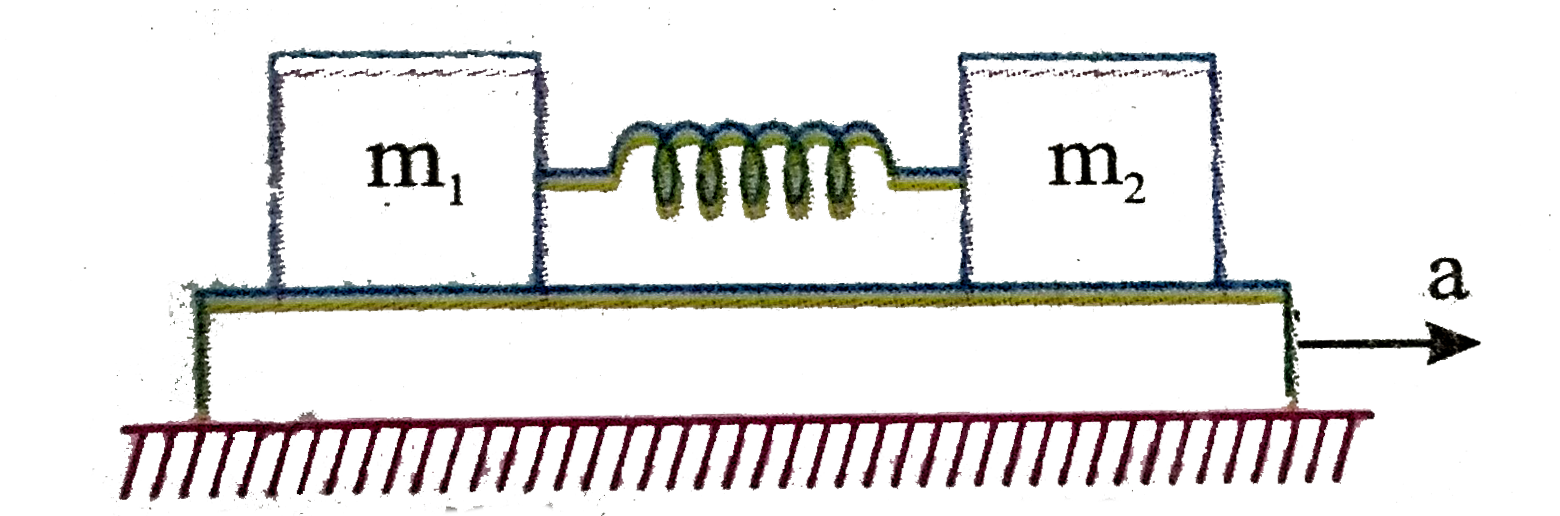
View SolutionA block of mass m slides down a rough inclined plane of inclination θ with horizontal with zero initial velocity. The coefficient of friction between the block and the plane is μ with θ>tan−1(μ). Rate of work done by the force of friction at time t is
View SolutionA solid block of mass m=1kg is reasting on a horizontal platform as shown in figure. The z direction is vertically up. Coefficient of friction between the block and the paltform is μ=0.2. The platform is moved with a time dependent velocity given →V=(2tˆi+tˆj+3ˆk)m/s. Then the magnitude of the net force exerted by the block on the platform is : (Take g=10m/s2)
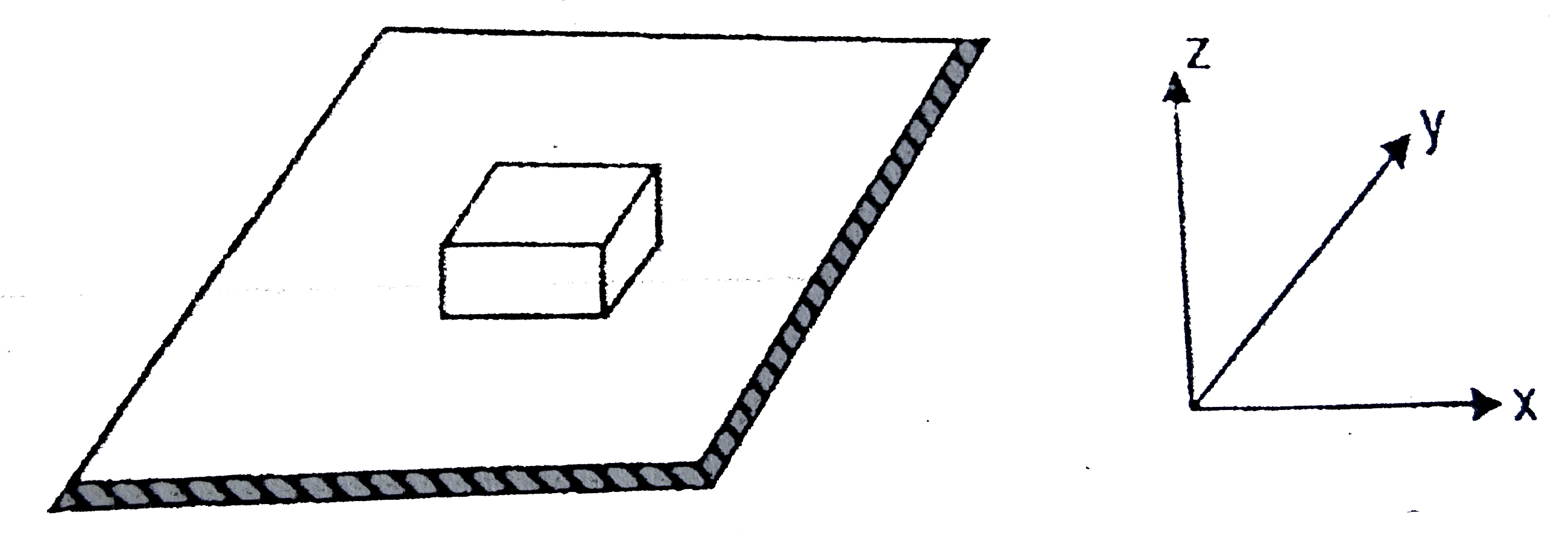
View SolutionA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When

View Solution
