There are two ideal springs of force constants K1 and K2 respectively. When both springs are relaxed the separation between free ends is L. Now the particle of mass m attached to free end of left spring is displaced by distance 2L towards left and then released. assuming the surface to be frictionless. (K1K2=43). (Neglect size of the block)

The maximum compression produced in right spring will be
6L/7
7L/6
L/3
2L/3
Time taken by particle to go from
x=0 to x=A/2 is T/12
∴ time interval =T2+T12=7T12
=712.2π√mK1=7π6√mK1
Assume, maximum compression in right spring is x. hence
12K1(2L)2=12K1(L+x)2+12K2x2
Put K2=34K1, we get x=6L7
When mass m in equilibrium both spring will be in extended state.
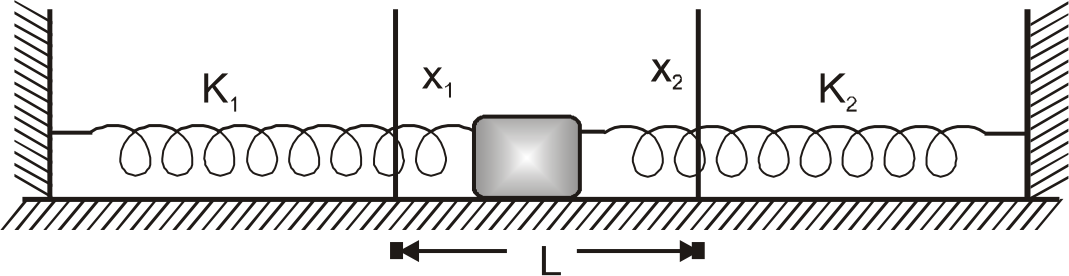
K1x1=K2x2 and x1+x2=L
x1=3L7.
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
04:45View SolutionWhen p−n junction diode is forward biased then
04:04View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards abnother block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 The spring constant of the spring fixed at one end is 10 N/m. Find the maximum compression of the spring.
05:37View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is mu then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
05:37View SolutionThere are two ideal springs of force constants K_1 and K_2 respectively. When both springs are relaxed the separation between free ends is L. Now the particle of mass m attached to free end of left spring is displaced by distance 2L towards left and then released. assuming the surface to be frictionless. ((K_(1))/(K_(2))=4/3) . (Neglect size of the block) The time interval after which mass 'm' hits the right spring will be
03:45View SolutionThere are two ideal springs of force constants K_1 and K_2 respectively. When both springs are relaxed the separation between free ends is L. Now the particle of mass m attached to free end of left spring is displaced by distance 2L towards left and then released. assuming the surface to be frictionless. ((K_(1))/(K_(2))=4/3) . (Neglect size of the block) Suppose mass m hits the right spring and sticks to it. The extension in left spring when mass ‘m’ is in equilibrium position during its motion is :
03:43View Solutionspring of force constant k clamped rigidly at onoe end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?
 03:46View Solution
03:46View Solutionचित्र 15.53 में एक द्रव्यमान M को दो स्प्रिंगों A तथा B से लटकाया गया है | स्प्रिंगों के बल नियतांक क्रमश : K1 तथा K2 हैं | दोनों स्प्रिंगों के खिंचावों का योग होगा :
 02:37View Solution
02:37View SolutionForce constants of two springs are k_1 and k_2 One end of a spring is connected with one end of the other. Equivalent force constant of the spring system will be
04:16View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released when the spring is initially unstretched. Then the maximum extension in the spring is
03:23View SolutionForce constants of two springs are k_1 and k_2 . One end of a spring is connected with one end of the other. Equivalent force constant of the spring system will be
02:49View SolutionFigure a) shows a spring of force constant k clamped rigidly at once end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in figure is stretched by the same force F.
(a) What is the maximum extension of the spring in the two cases ?
(b) If the mass in figure and the two masses in figure are released free, what is the period of oscillation in each case?
 04:05View Solution
04:05View SolutionFigure 14.26 (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure 14.26 (b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in Fig. 14.26(b) is stretched by the same force F.

What is the maximum extension of the spring in the two cases ?03:22View Solution6kg तथा 3kg द्रव्यमान के दो ब्लॉक 2π2N/m स्प्रिंग नियतांक की द्रव्यमानहीन स्प्रिंग के दोनों सिरो से जड़े हुए हैं। यदि स्प्रिंग संपीडीत की जाती है तथा घर्षणरहित क्षैतिज सतह पर छोड़ी जाती है तो प्रत्येक ब्लॉक का आवर्त काल (सैकण्ड में) ज्ञात करो।
04:35View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is mu then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
04:56View Solution

