The limbs of a manometer consists of uniform capillary tubes of radii 1.44×10−3m and 7.2×104m. If the level of the liquid in the narrower tube stands 0.2 m above that in the broader tube, pressure difference between A and B is found to be 310λN/m2. Here λ is an integer. Find λ (density = 103kg/m3, surface tension = 72×10−3N/m). (take g=9.8m/s2)
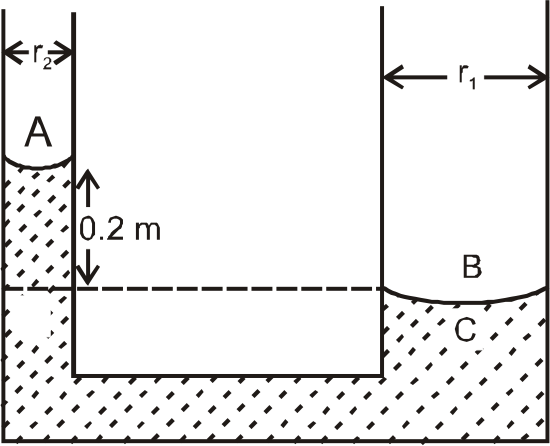
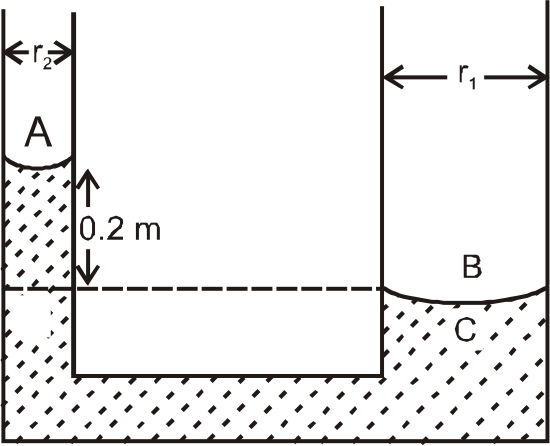
r1=1.44×10−3m,r2=0.72×10−3m
Equating pressures at points (B) and C
PA−2σr2+(0.2)ρg=PC and PB−2σr1=PC
so PB−PA=2σ(1r1−1r2)+0.2ρg
=2×72×10−3Nmp[10−31.44−1030.72]+(0.2)×103×938
=144×(−0.72)1.44×0.72+1960=−100+1960=1860N/m2.
Topper's Solved these Questions
Similar Questions
The limbs of a manometer consist of uniform capillary tubes of radii are 10−3&7.2×10−4m find out the correct pressure difference if the level of the liquid in narrower tube stands 0.2 m above that in the broader tube. (density of liquid =103kg/m3, surface tension =72×10−3N/m)
View SolutionA barometer contains two uniform capillries of radii 1.44×10−3m and 7.2×10−4m. If the height of the liquid in the narrow tube is 0.2m more than that in the wide tube, calculate the true pressure difference. Density of liquid =103kg/m3, surface tension =72×10−3N/m and g=m/s2.
View Solution
Knowledge Check
Water rises in a capillary tube of diameter 0.2×102m upto a height of 1.5 cm. The surface tension of water is-
A73.5×101N/mB73.5×10−3dyne/cmC35.7×10−3N/mD43.5×10−3A capillary tube of radius r can support a liquid of weight 6.28×10−4N. If the surface tension of the liquid is 5×10−2N/m. The radius of capillary must be
A2×10−3mB2×10−4mC1.5×10−3D12.5×10−4mTwo seperate soap bubbles of radii 3×10−3 m and 2×10−3 m respectively, formed of same liquid (surface tension 6.5×10−2 N/m) come together to form a double bubble. The radius of interface of doubl bubble is
A6×10−3 mB4×10−3 mC1.5×10−3 mD0.66×10−3 m
A barometer contains two uniform capillaries of radii 1.4×10−3m and 7.2×10−4m. If the height of liquid in narrow tube is 0.2m more than that in wide tube, calculate the true pressure difference. Density of liqid =103kg/m3, surface tension =72×10−3N/m and g=9.8ms−12.
View SolutionMercury in a capillary tube suffers a depression of 13.2 mm. Find the diameter of the tube. If angle of contact of mercury is 140∘ and density 13.6×103kgm−3 Surface tension of mercury is 540×10−3Nm−1
View SolutionA glass capillary tube of inner diameter 0.28mm is lowered verically into water in a vessel. The pressure to be applied on the water in the capillary tube so that water level in the tube is same as that in the vessel is λ×105N/m2. Then find λ in nearest integer (surface tension of water =0.07N/m and atmospheric pressure =105N/m2) :
View SolutionThe surface energy of a soap film formed on a frame of area 2×10−3m2is(T=40×10−3 N/m)
View SolutionA capillary tube of internal radius 2×10−3 m immersed vertically in beaker containing a liquid rising in the capillary tube is 9×105 kg , the surface tension of the liquid is
View Solution