In the figure , M is the midpoint of QR .
∠PRQ=90∘.
Prove that ,
PQ2=4PM2−3PR2 .
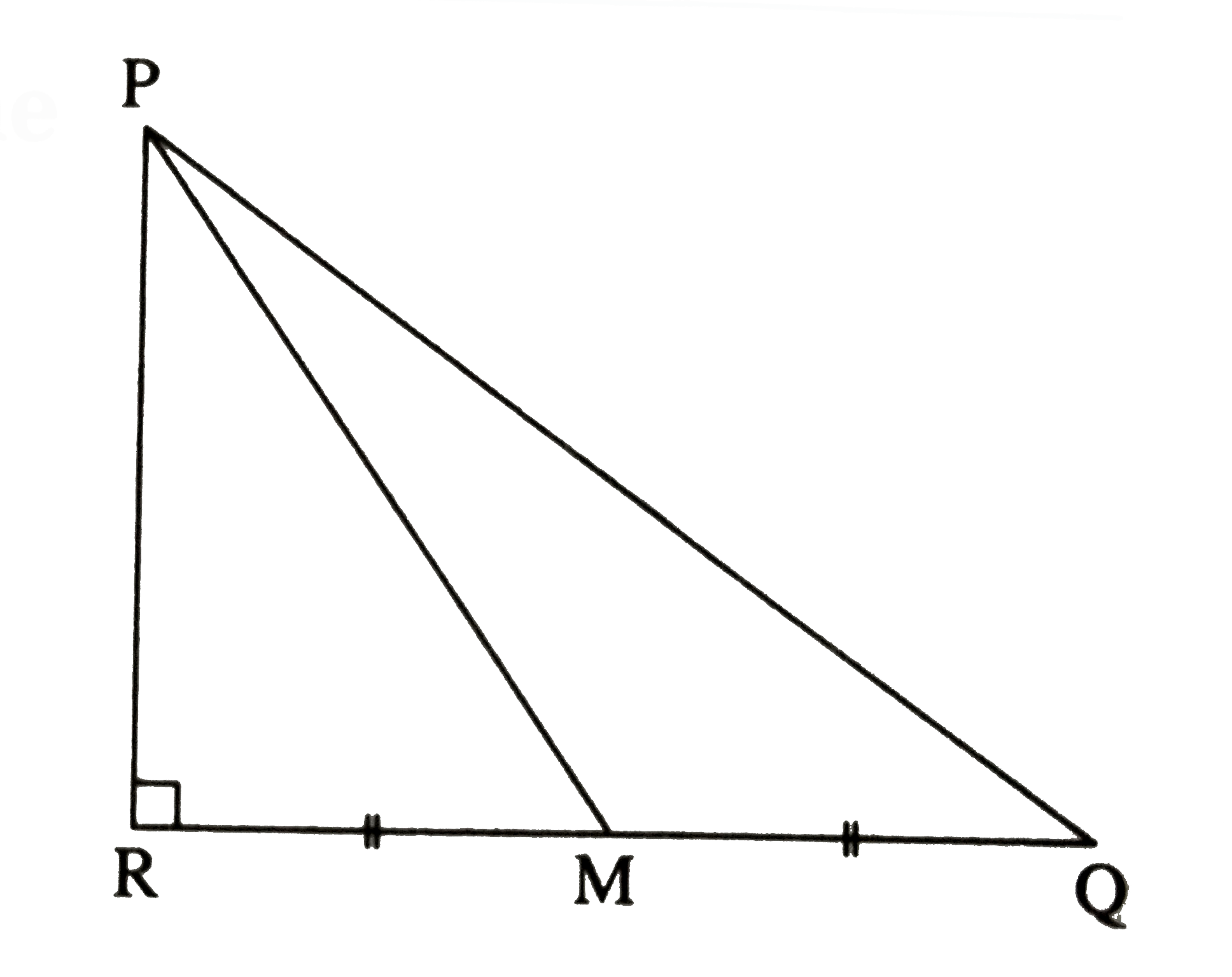
The correct Answer is:PQ2=4PM2−3PR2 .
Step by step video & image solution for In the figure , M is the midpoint of QR . angle PRQ = 90^(@). Prove that , PQ^(2) = 4PM^(2) - 3PR^(2) . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - PRACTICE SET 2.2
5 Videos
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - PROBLEM SET-2
30 Videos
- PYTHAGORAS THEOREMBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PYTHAGORAS THEOREMEXERCISE - EXAMPLES FOR PRACTICE ( 2 MARK QUESTIONS )
2 Videos
- PROBABILITY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY EXERCISE - ASSIGNEMENT 5.4
12 Videos
- QUADRATIC EQUATION BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUADRATIC EQUATION EXERCISE - CHALLENGIN QUESTIONS
2 Videos
Similar Questions
In the given figure, M is the midpoint of QR. ∠PQR=90∘.
Prove that, PQ2=4PM2−3PR2.
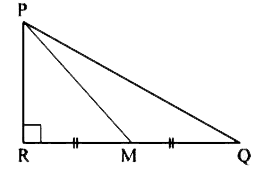
View SolutionIn the figure, M is the midpoint of QR. ∠PRQ=90∘. Prove that PQ2=4PM2−3PR2
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
View SolutionIn adjoining figure, seg PS is the median of ΔPQRadnPT⊥QR. Prove that
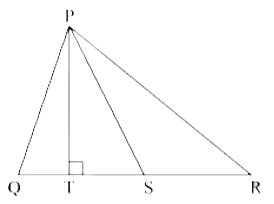
(1) PR2=PS2+QR×ST+(OR2)2
(2) PQ2=PS2+QR×ST+(QR2)2
View SolutionIn PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
View SolutionIn ΔPQR, point S is the midpoint of side QR. If PQ =11, PR =17 PS =13 , find QR.
View Solution
In the figure , S is the midpoint of seg PQ . Line ST || side QR and PT =5 cm , then find PR. Justify your answer.
View SolutionIn the given figure, PR > PQ and PS bisects ∠ QPR. Prove that ∠PSR>∠PSQ.
View Solution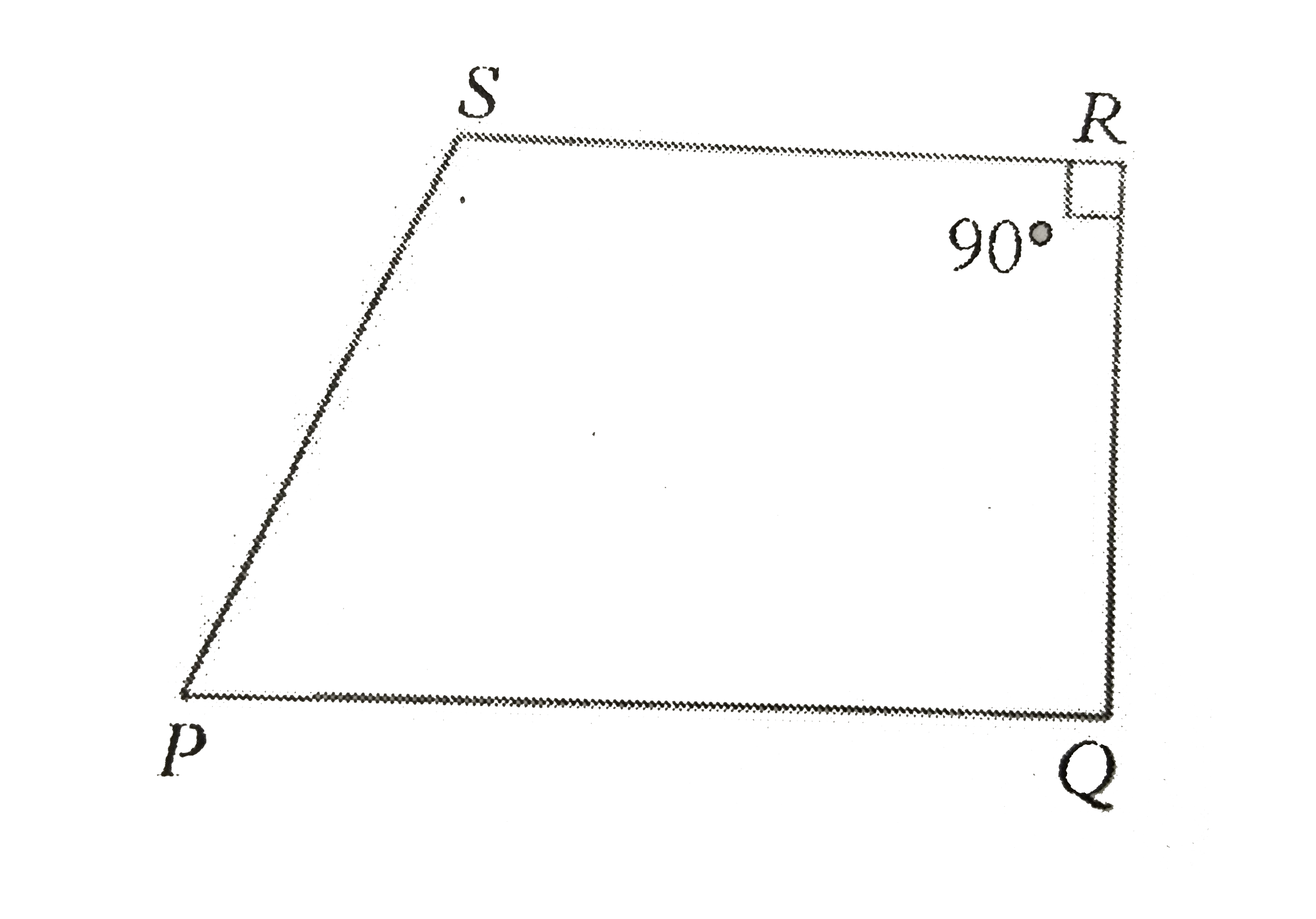
In the figure above, PQRS is a trapezium , PQ//SR, QR=RS, and ∠QRS=90∘. If QR=24 cm and PS=25 cm , then find the length of PQ.
View SolutionIn the adjoining figure, PQR, is a right triangle, right angled at Q. X and Y are the points on PQ and QR such that PX:XQ=1:2 and QY:YR=2:1. Prove that 9(PY2+XR2)=13PR2
View Solution
