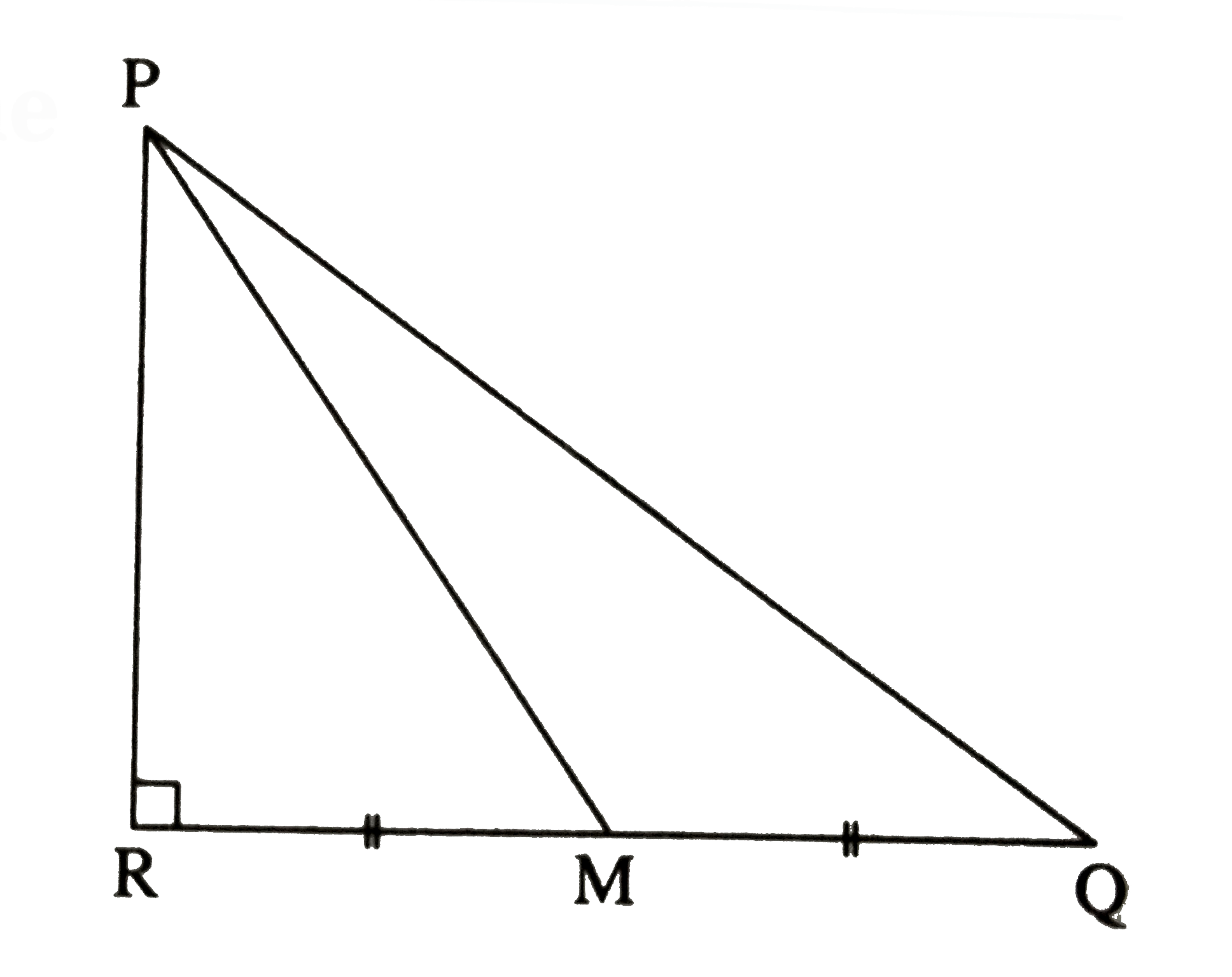
In the given figure, M is the midpoint of QR. ∠PQR=90∘.
Prove that, PQ2=4PM2−3PR2.
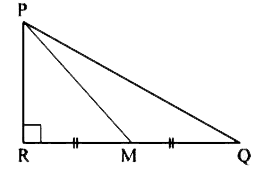
The correct Answer is:PQ2+PR2=4PM2−2PR2
Topper's Solved these Questions
- PYTHAGORS THEORMBOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - PRACTICE SET 2.2
4 Videos
- PYTHAGORS THEORMBOOK - UNIQUE PUBLICATIONCHAPTER - PYTHAGORS THEORMEXERCISE - PROBLEM SET 2
30 Videos
- PROBABILITY BOOK - UNIQUE PUBLICATIONCHAPTER - PROBABILITY EXERCISE - PROBLEM SET 5
23 Videos
- QUADRATIC EQUATIONS BOOK - UNIQUE PUBLICATIONCHAPTER - QUADRATIC EQUATIONS EXERCISE - ASSIGNMENT
6 Videos
Similar Questions
Knowledge Check
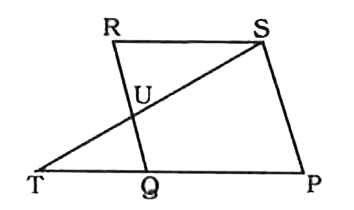
In the given figure, PQRSis a parallelogram and U is the mid point of QR. If PQ=4cm, then what is the value of PT (in cm.)?
 A6B6.5C7.5D8
A6B6.5C7.5D8
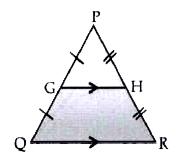
In the given figure G is the mid-point of the side PQ of ΔPQR and GH || QR .Prove that H is the mid -point of the side PR of the triangle PQR .
View SolutionIn the given figure, seg PM is a median of ΔPQR.PM=9andPQ2+PR2=290, then find QR.

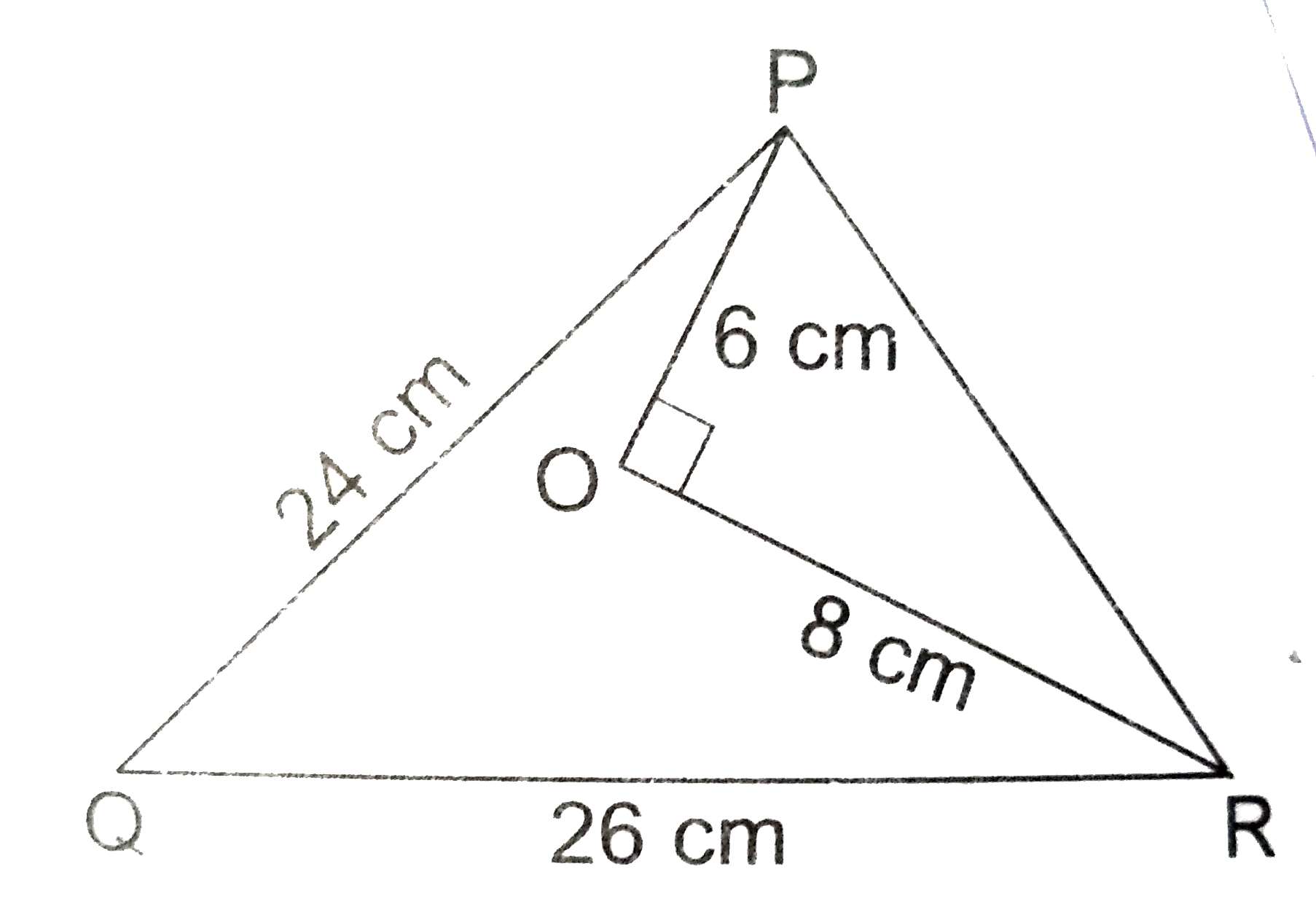
View SolutionIn the given figure, O is point inside a ΔPQR such that ∠POR=90∘,OP=6cmandOR=8cm. If PQ=24cmandQR=26cm, prove that ΔPQR is right angled.
View SolutionM and N are mid point on sides QR and PQ respectively of △PQR, right-anggled at Q. Prove that :
4PM2=4PQ2+QR2.
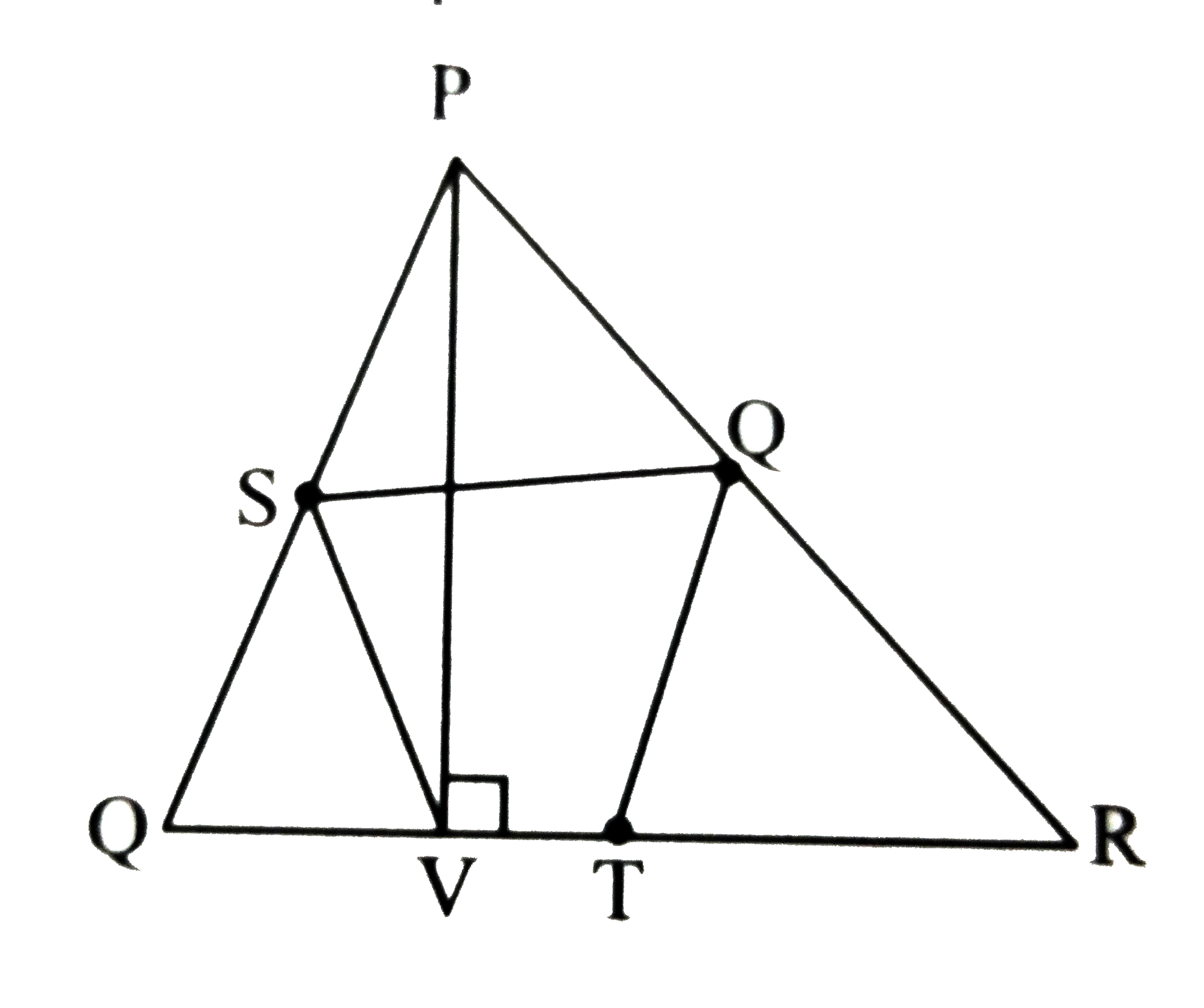
View SolutionIn the given figure, points S,T and U are the midpoints of sides PQ,QR and PR respectively. IF PV⊥QR, then prove that □ SVTU is a cyclic quadrilateral.
View SolutionIn PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
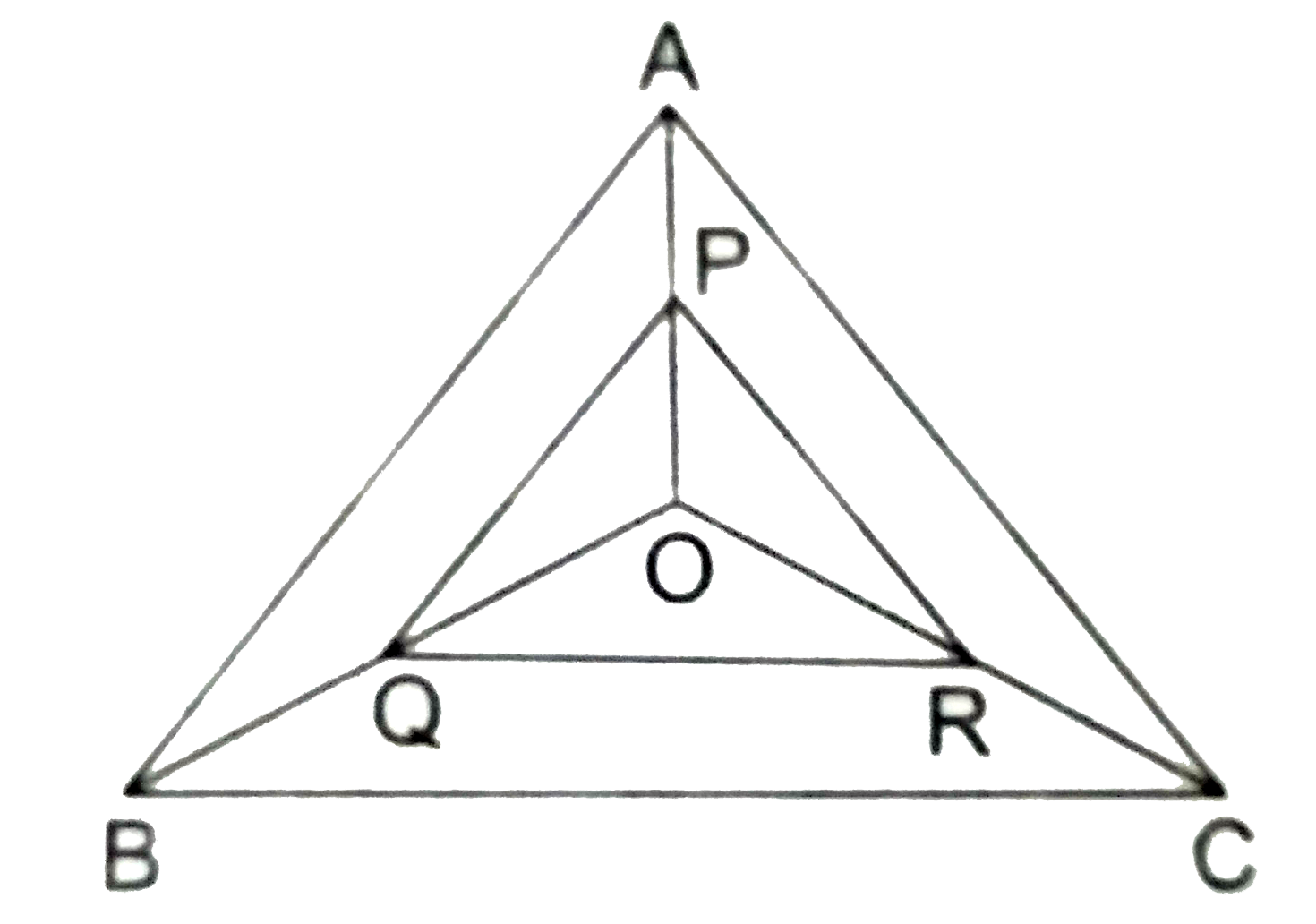
View SolutionIn the given figure, PQ||ABandPR||AC.
Prove that QR∣∣BC
View Solution