The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
Video Solution
|
Answer
Step by step video & image solution for The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PROBLEM SET 3
50 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
Knowledge Check
The quadrilateral formed by the bisectors of the angles of a parallelogram is a
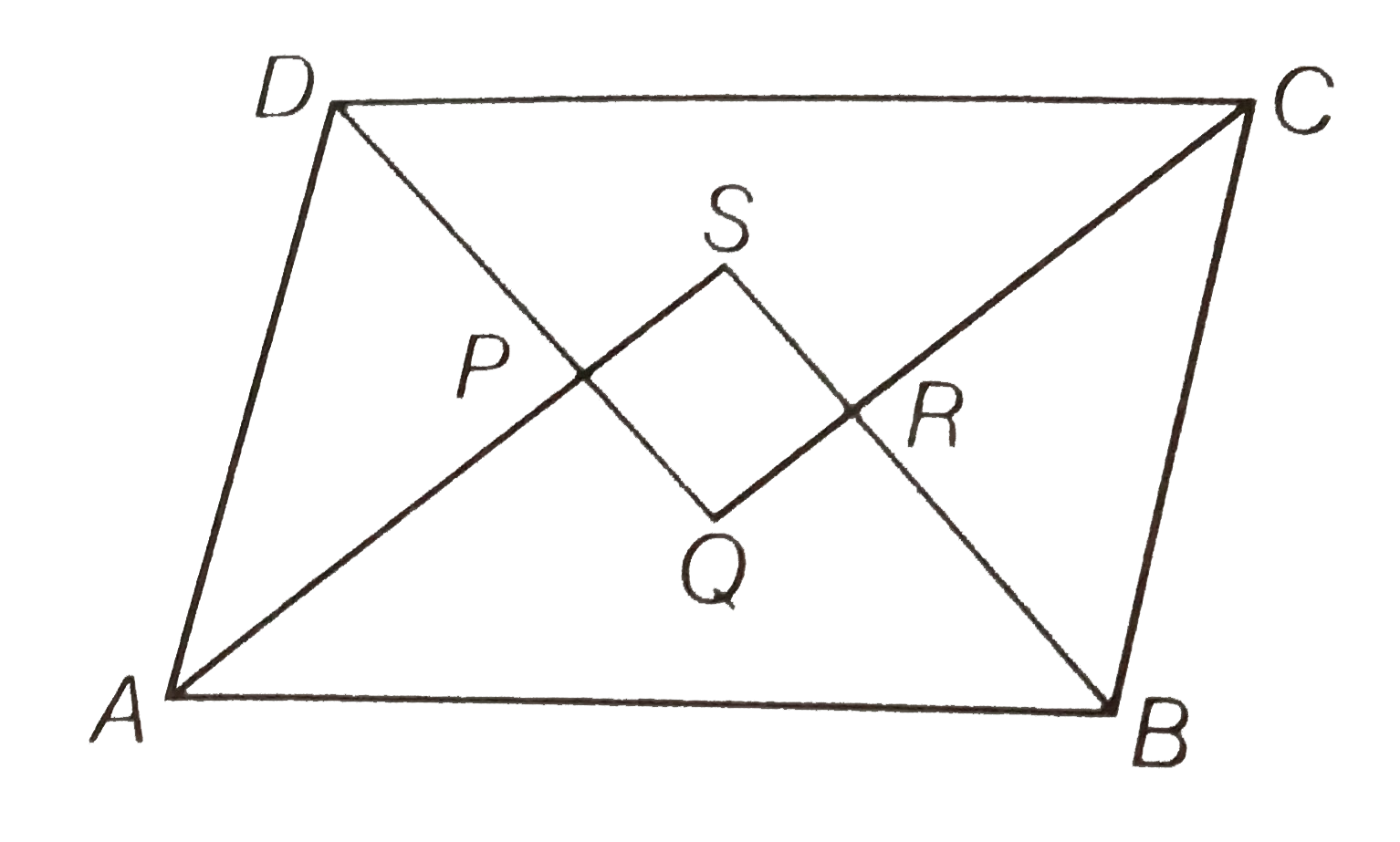 ArectangleBsquareCparallelogramDcyclic quadrilateral
ArectangleBsquareCparallelogramDcyclic quadrilateralWhich of the following statements is/are correct?
The intersections of the angle bisectors of the quadrilateral are the vertices of the cyclic quadrilateral
If diagonals of a cyclic quadrilateral perpendicularly intersect at point P, then the line through P, perpendicular to any side bisects the opposite side.
The product of the lengths of the two diagonals of a cyclic quadrilateral is equal to the sum of the products of opposite sides.A(i) and (ii)B(ii) and (iii)C(i) and (iii)Dall of theseThe quadrilateral formed by the bisectors of the angles of a parallelogram is a
 ATrapeziumBKiteCRectangleDNone
ATrapeziumBKiteCRectangleDNone
Prove that, any rectangle is a cyclic quadrilateral.
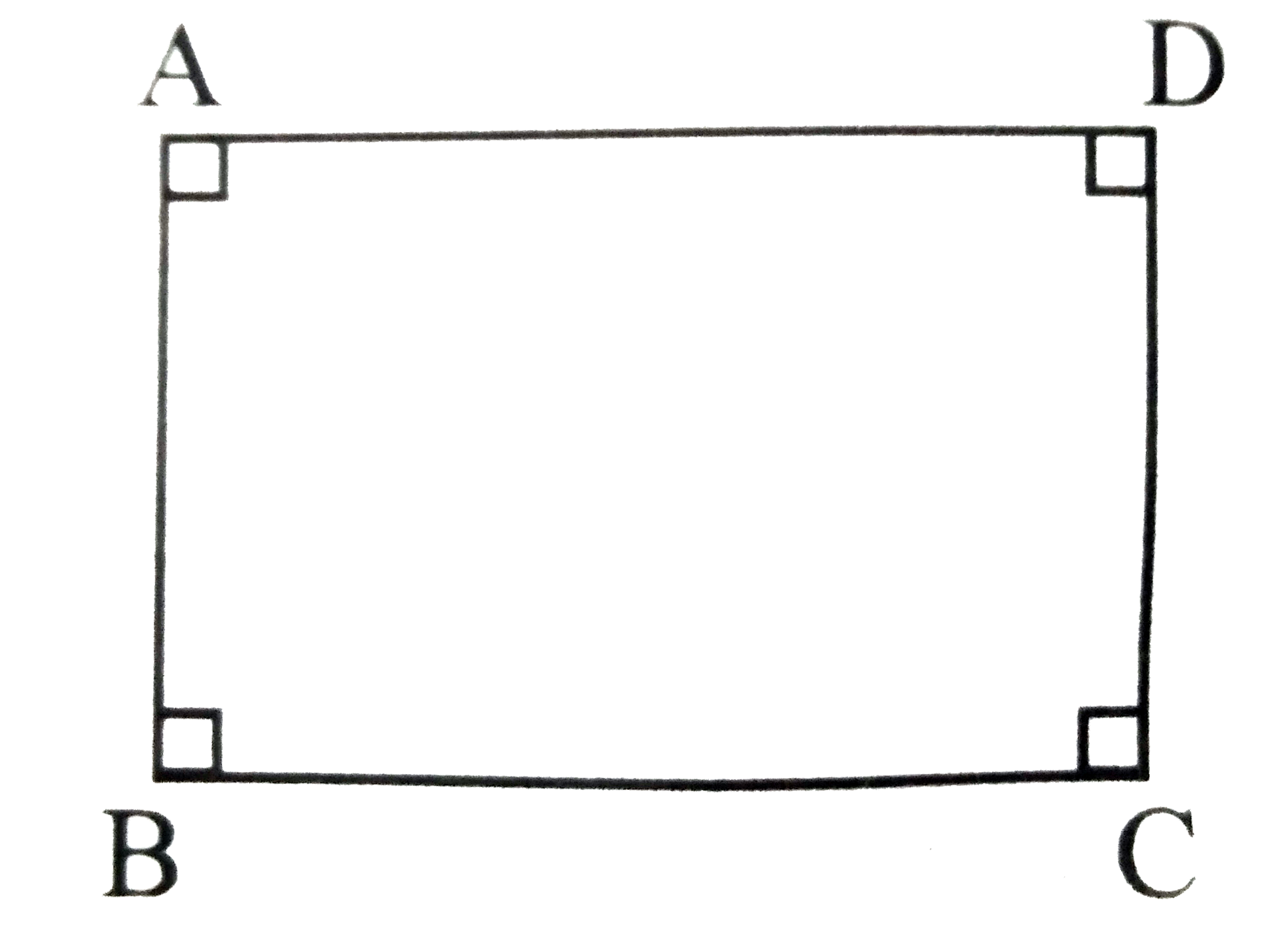
View SolutionProve that, any rectangle is a cyclic quadrilateral.
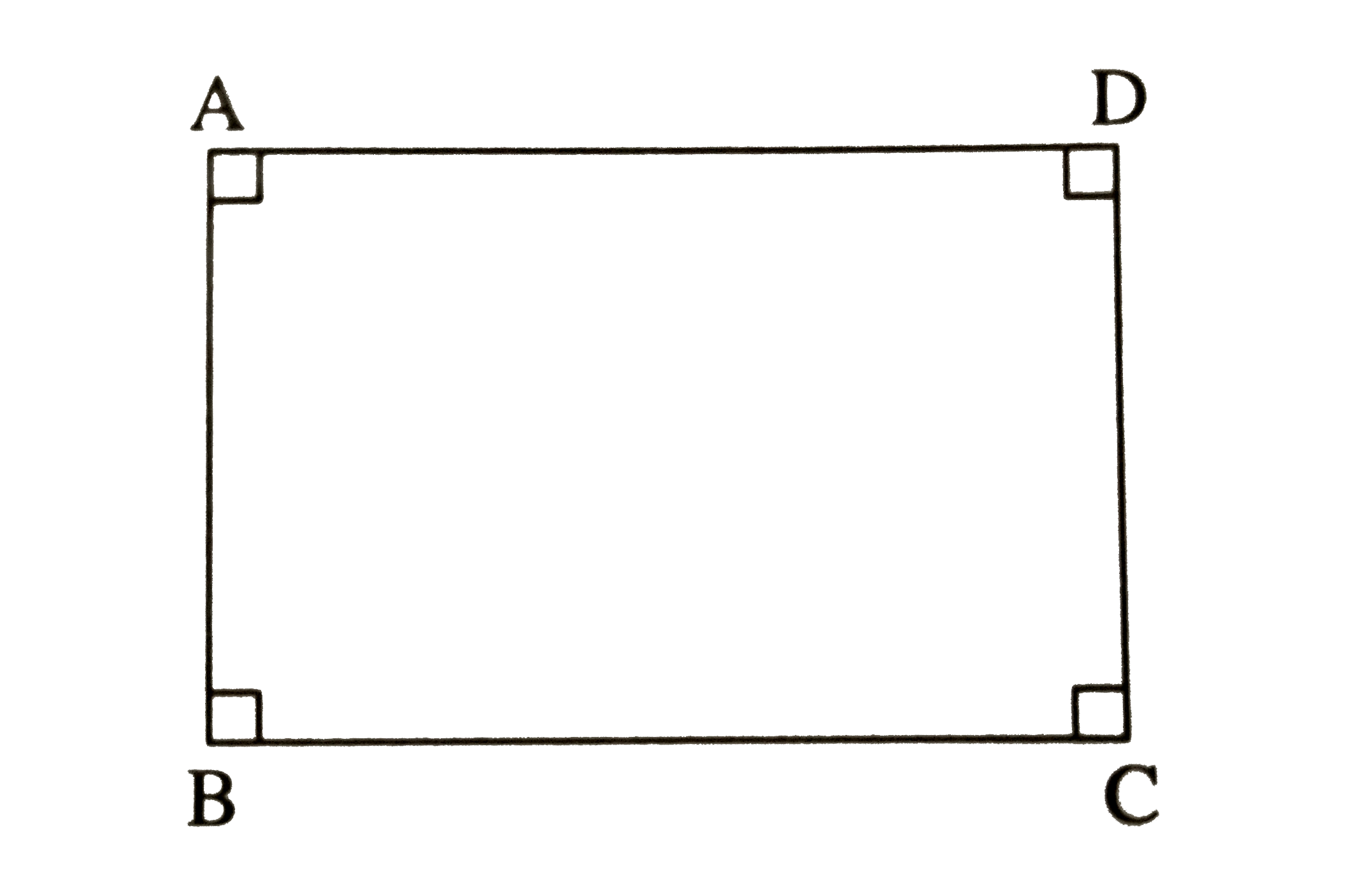
View SolutionProve that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
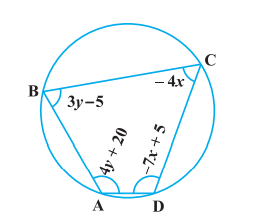
View SolutionABCD is a cyclic quadrilateral (see Figure). Find the angles of the cyclic quadrilateral.
View SolutionThe bisectors of the angles formed by producing the opposite sides of a cyclic quadrilateral (provided that they are not parallel) intersect at right angle.
View Solution
