In the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove ∠CPA≅∠DPB.
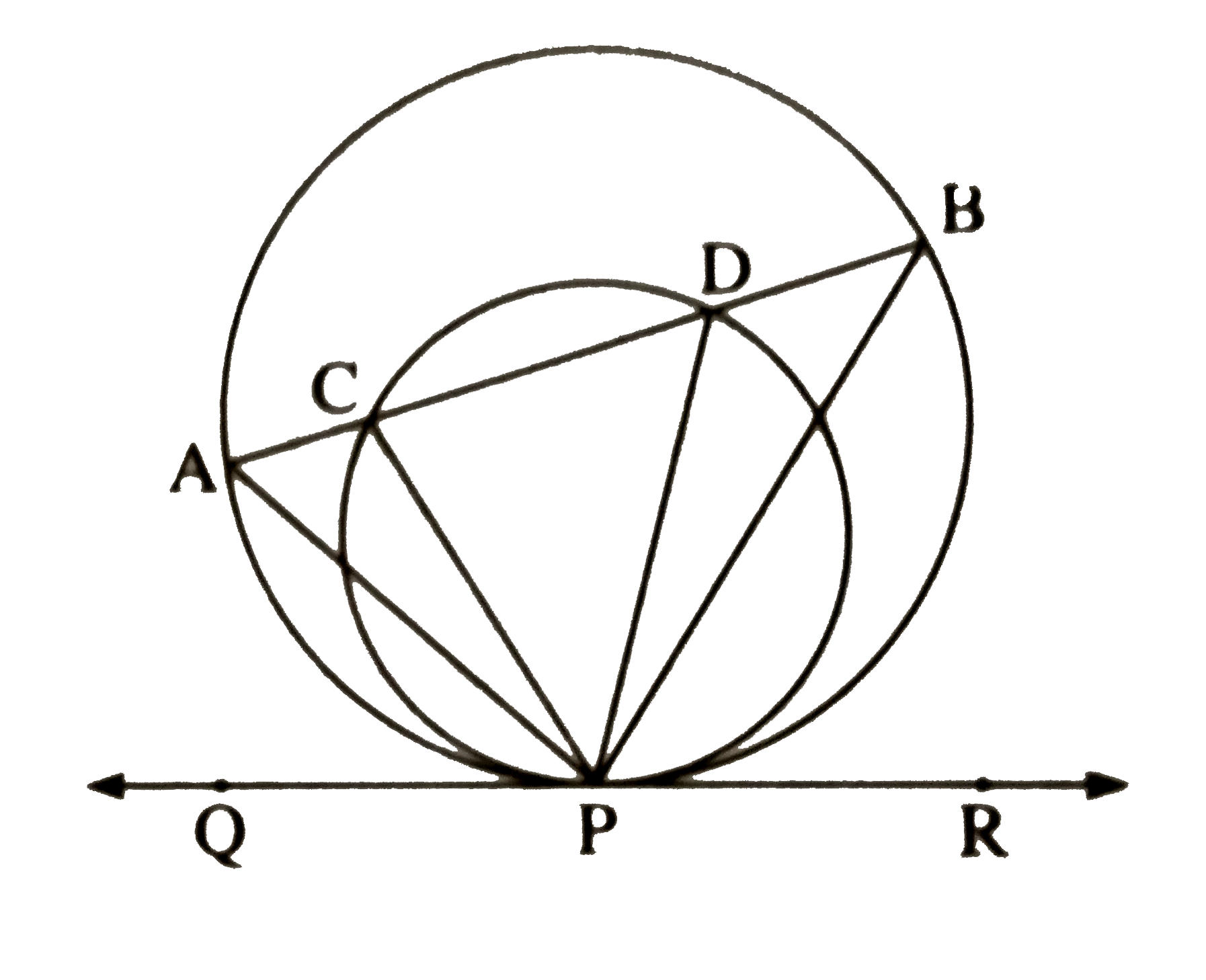
Step by step video & image solution for In the figure, two circles touch internally at point P. chord AB of the larger circle intersects the smaller circle in C and D. Prove /_CPA cong /_DPB. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PROBLEM SET 3
50 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
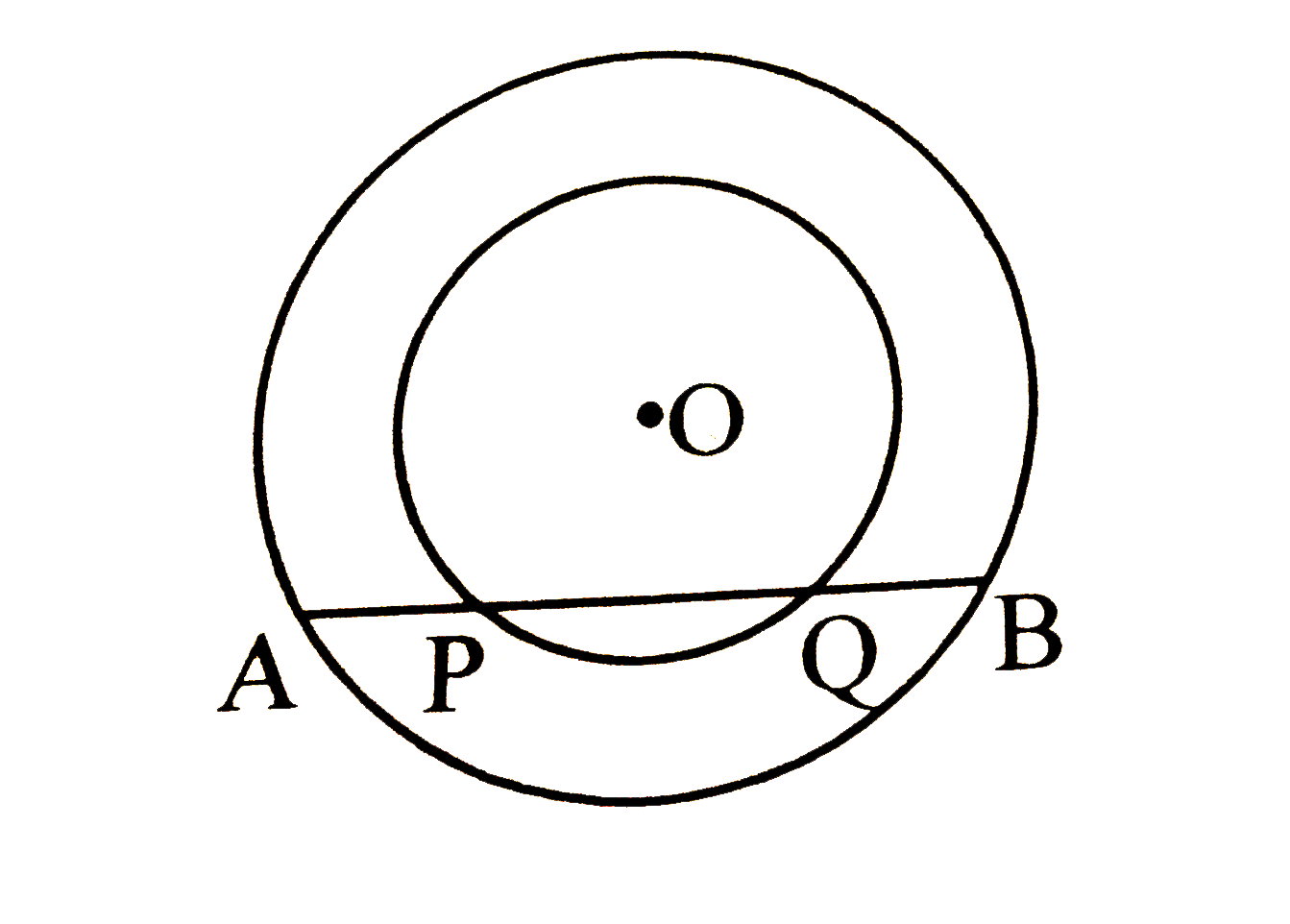
In the given figure, centre of two circles is O. Chord AB of bigger circle intersects the smaller circle in points P and Q . Show that AP = BQ.
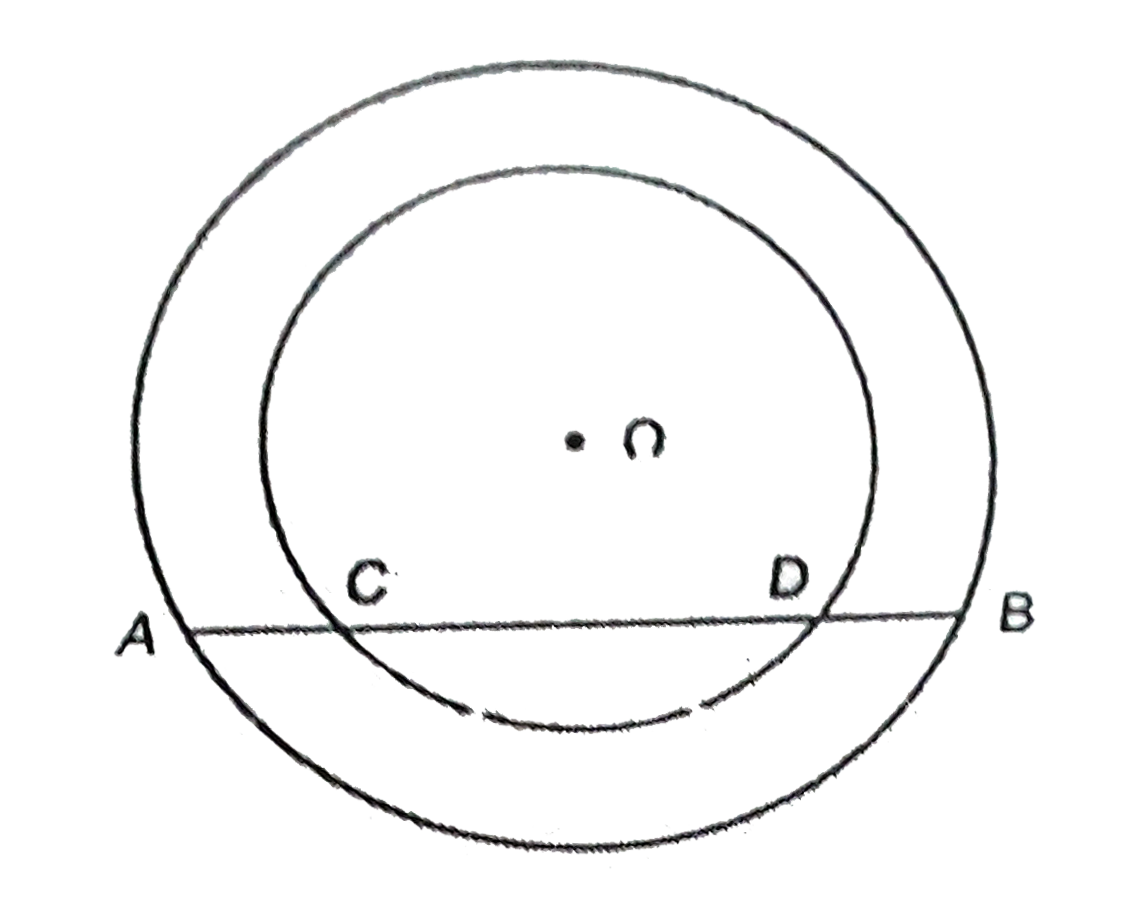
View SolutionIn the adjoining figure,O is the centre of two concentric circles. The chord AB of larger circle intersects the smaller circle at C and D.
(i) Find AC:BD.
(ii) If AC=2cm, then find the length of BD.
View Solution
Knowledge Check
Let two chords AB and AC of the larger circle having same centre touch the smaller circle having same centre at X and Y. Then XY = ?
ABCB12BCC13BCD14BC
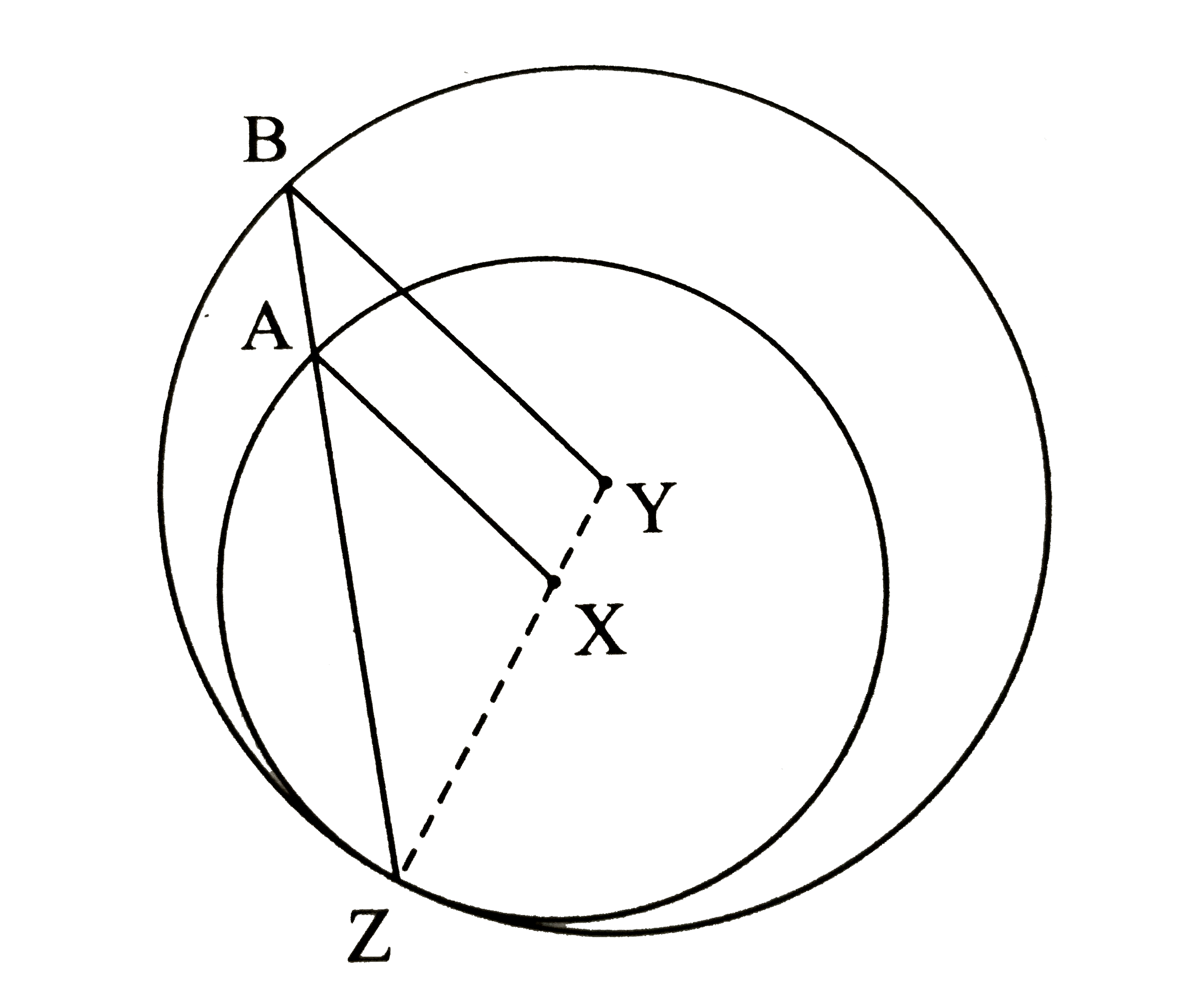
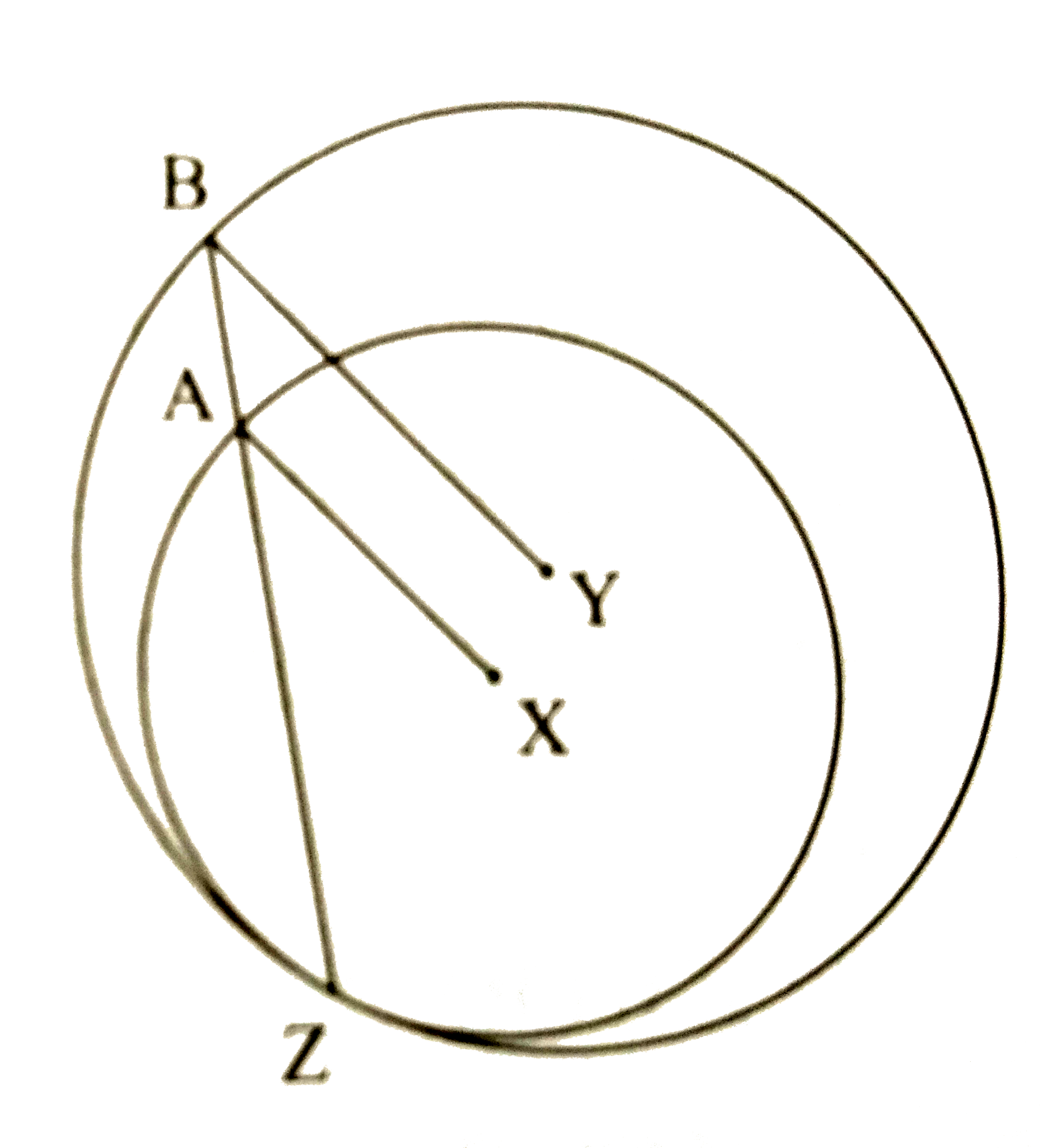
In the figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circle at point A. Prove that, seg AX || seg BY.
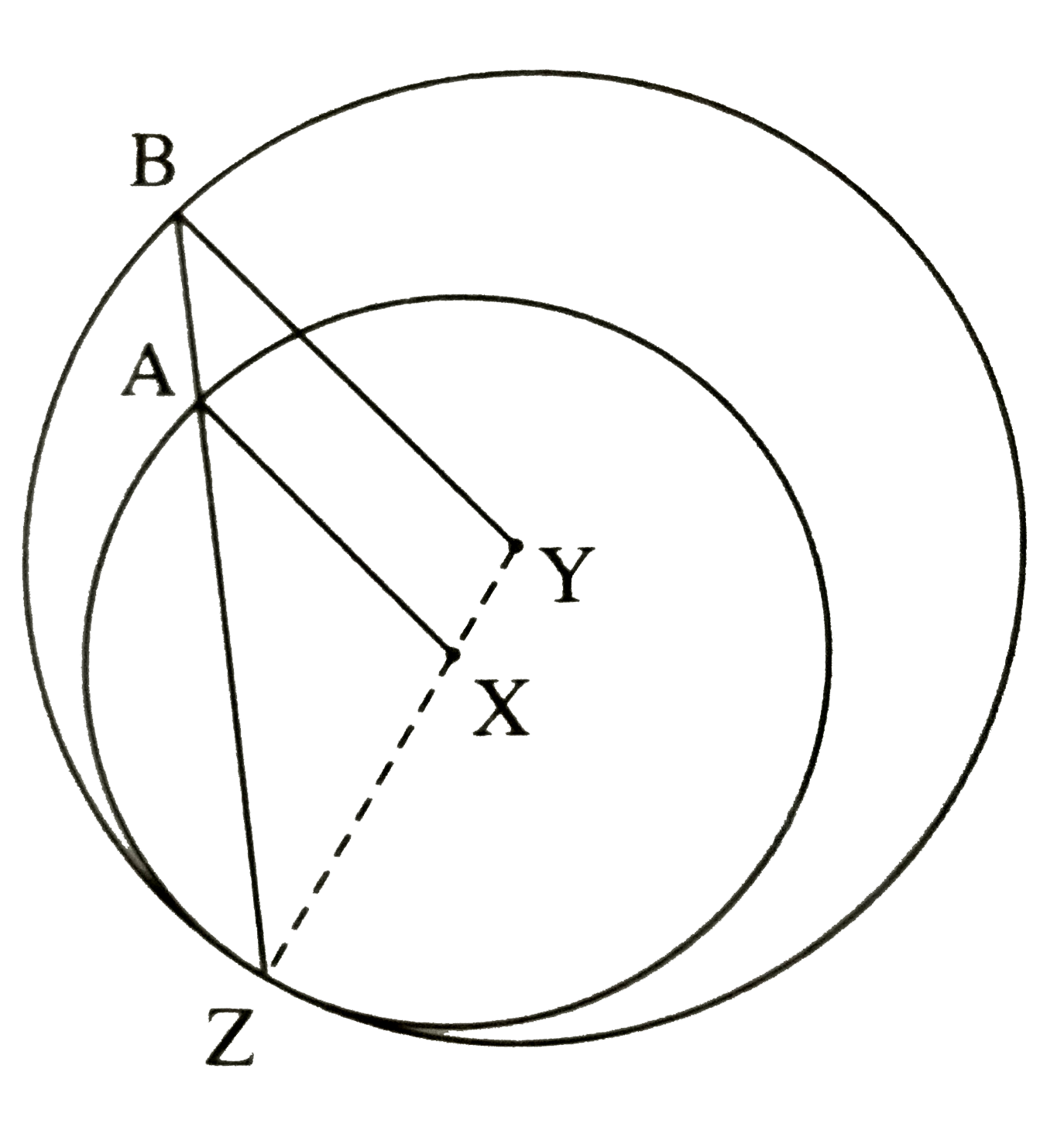
View SolutionIn the figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circlea t point A. Prove that , seg AX ∣∣ seg BY
View SolutionIn the figure , two concentric circles of radii a&b(a>b) are given.The chord AB of larger circle touches the smaller circle at C .The length AB is :
View SolutionIn the figure , circles with centres X and Y touch internally at point Z. Seg BZ is the chord of bigger circle and it intersects smaller k circle at point A.
Prove that seg AX∣∣ seg BY.
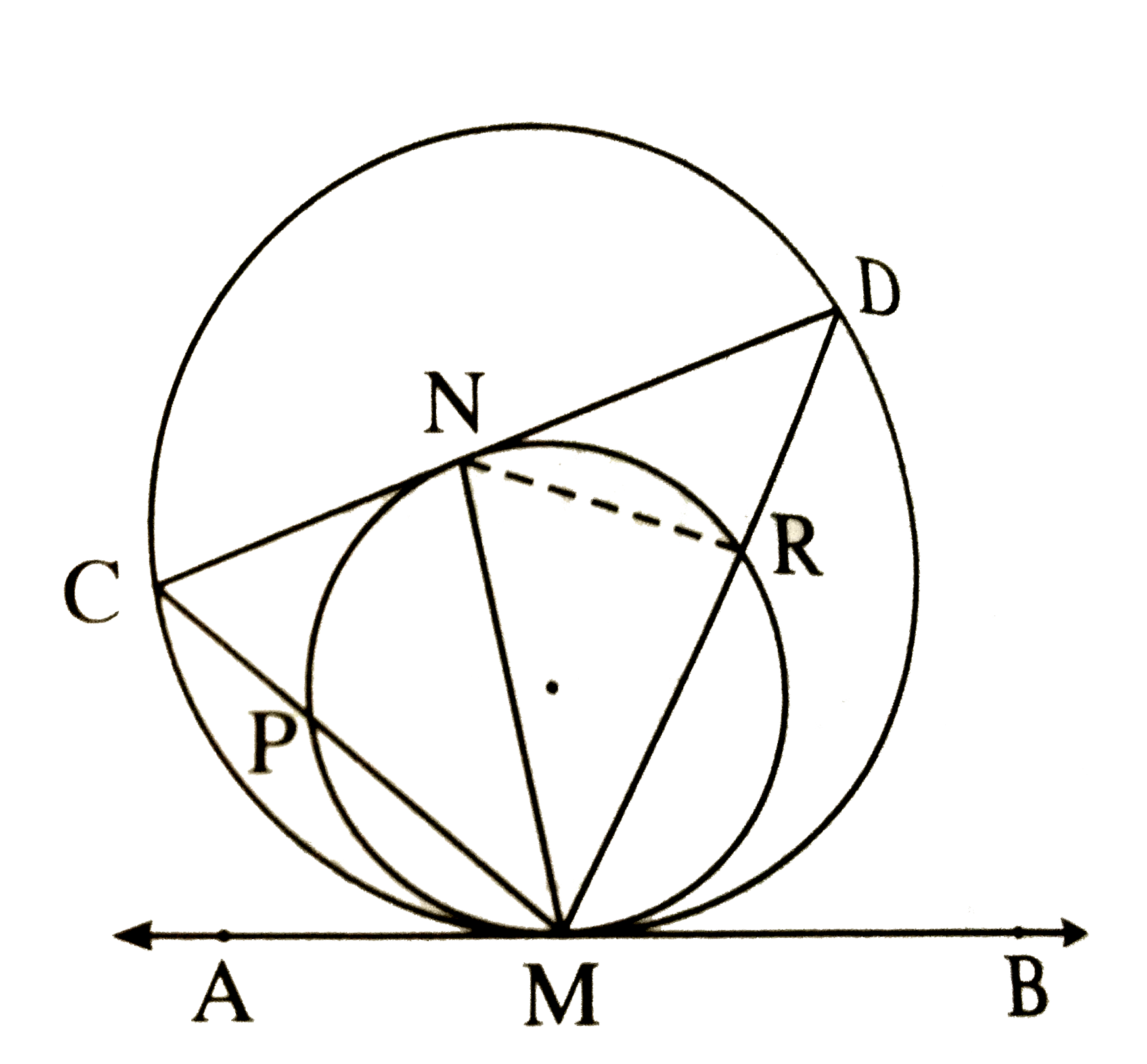
View SolutionLet M be a point of contact of two internally touching circles. Let line AMB be their common tangent. The chord CD of the bigger circle touches the smaller circle at the point N. Chord CM and chord DM of the bigger circler intersect the smaller circle at the points P and R respectively.
Prove that ∠CMN≅∠DMN.
Construction : Draw seg NR.
View SolutionTwo circles are tangent internally at P and a chord, AB of the larger circle is tangent to the smaller circle at C. PB and PA cut the smaller circle at E and D, respectively. If AB = 15 cm, While PE = 2 cm and PD = 3 cm. Find AC
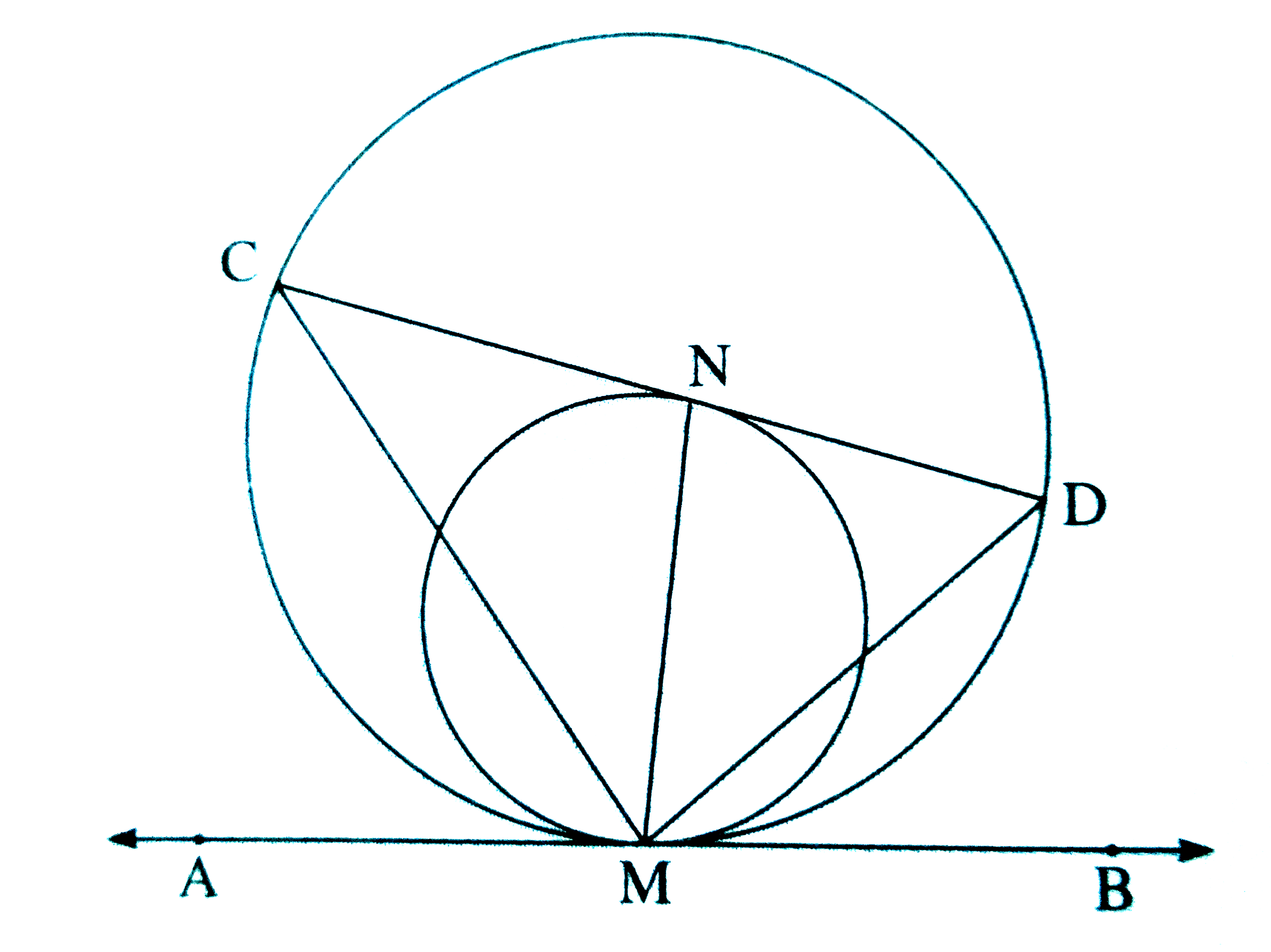
View SolutionIn the figure, M is the point of contact of two internally touching circles. The chord CD of the bigger circle touches the smaller circle at point N. Line AMB is their common tangent. Prove MN bisects ∠CMD
View Solution
