A particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
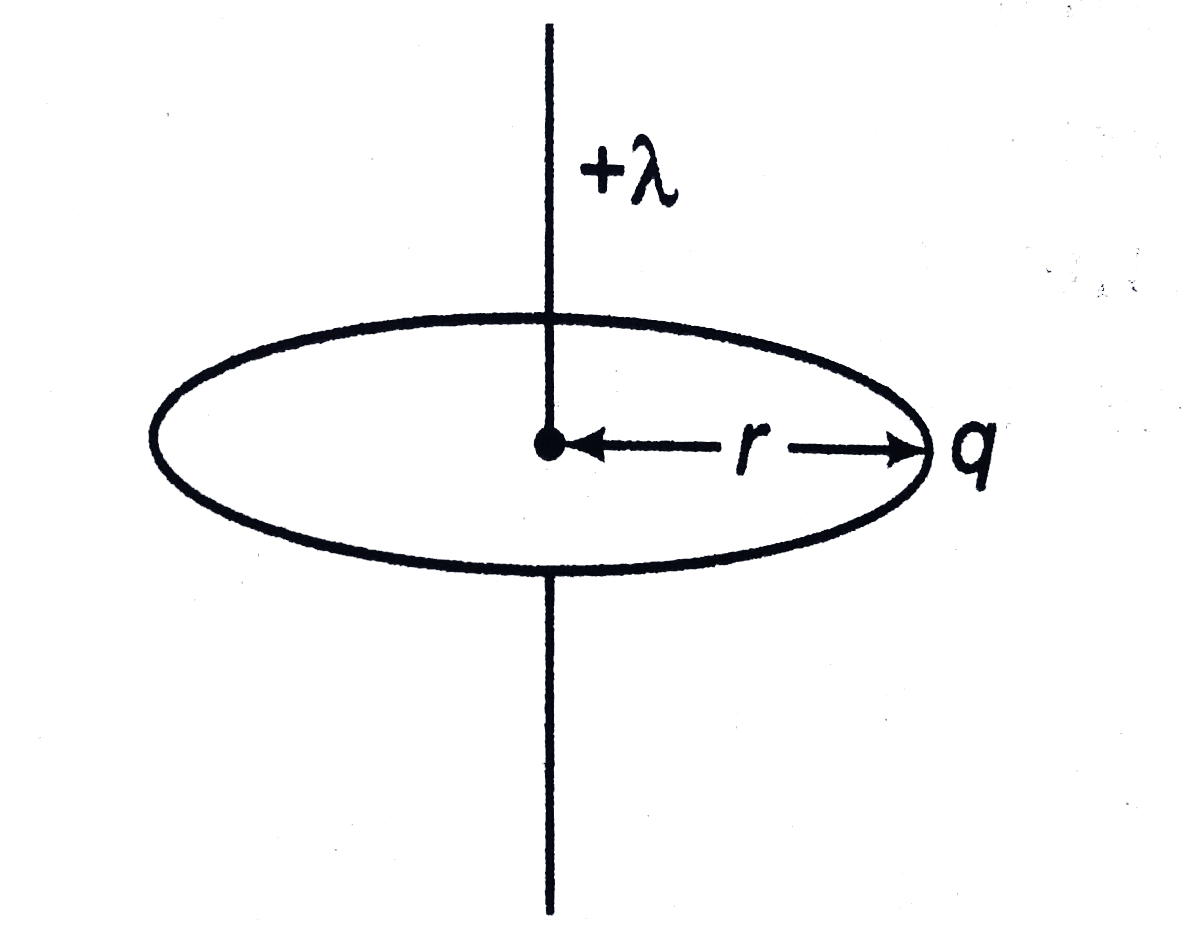 where , k=14πε0)
where , k=14πε0)
T=2πr√m2kλq
T2=4π2m2kλq
T=12πr√2kλqm
TT=12πr√m2kλq
The correct Answer is:a
mv2R=qλ2πε0r⇒v=√qλ2πε0m=√2kqλm
T=2πrv=2πr√m2kqλ
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section B - Assertion Reasoning25videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - AIPMTNEET Questions24videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Electric Dipole29videos
ELECTRIC CHARGE, FIELD & FLUX
- BOOK - A2ZCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Section D - Chapter End Test30videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Section D - Chapter End Test29videos
ELECTRIC POTENTIAL & CAPACITANCE
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle of charge −q and mass m moves in a circular orbits of radius r about a fixed charge +Q.The relation between the radius of the orbit r and the time period T is
Ar=Qq16π2ε0MT3Br3=Qq16π2ε0MT2Cr2=Qq16π3ε0mT3Dr2=Qq16π3ε0mT3 - Question 2 - Select One
A charge moves with a speed v in a circular path of radius r around a long uniformly charged conductor.
Av∝rBv∝1rCv∝1√rDv∝r0 - Question 3 - Select One
Find ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
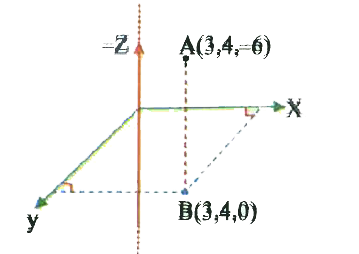 A1:2B1:6C6:1D1:1
A1:2B1:6C6:1D1:1
A particle of charge q1 and mass m is revolving around a fixed negative charge of magnitude q2 in a circular path of radius r. Find the time period of revolution.
View SolutionA charged particle q of mass m is in wquilibrium at a height h from a horizontal infinite line charge wit uniform linear charge density λ. The charge lies in the vertical plane containing the line charge. If the particle is displaced slightly (vertically) prove that the motion of the charged particle will be simple harmonic. Also find its time period.
View SolutionOn rotating a point charge g around a charge Q in a circle of radius r, the work done is
View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
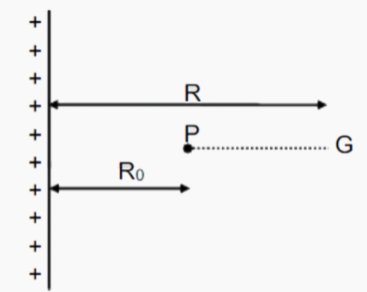 View Solution
View SolutionA charge particle (charge q ) is moving in a circle of radius R with uniform speed. v The associated magnetic moment m is given by
View Solution

