A straight section PQ of a circuit lies along the X-axis from x=−a2 to x=a2 and carriers a steady current i. The magnetic field due to the section PQ at a point X=+a will be
Proportional to a
Proportional to a2
Proprotional to 1/a
Zero
The correct Answer is:D
To find the magnetic field at point X=+a due to the straight section PQ of the circuit carrying a steady current i, we can use the Biot-Savart law. Here’s a step-by-step solution:
Step 1: Understand the Setup
The straight section PQ of the circuit lies along the X-axis from x=−a2 to x=+a2. The current i flows through this section.
Step 2: Identify the Point of Interest
We need to calculate the magnetic field at the point X=+a, which is located to the right of the wire segment PQ.
Step 3: Apply the Biot-Savart Law
The Biot-Savart law states that the magnetic field dB at a point due to a current element Idl is given by:
dB=μ04πIdl×^rr2
where:
- μ0 is the permeability of free space,
- dl is the current element,
- ^r is the unit vector from the current element to the point where the field is being calculated,
- r is the distance from the current element to the point.
Step 4: Determine the Geometry
For a small segment dl at position x along the wire, the distance r to the point X=+a is:
r=a−x
The angle θ between dl and ^r can be determined from the geometry of the setup.
Step 5: Calculate the Angle
Since dl is along the X-axis and ^r points from the wire to the point X=+a, the angle θ between dl and ^r is 0∘ for all points along the wire (since both are along the same line).
Step 6: Evaluate dl×^r
Since θ=0∘, we have:
dl×^r=dl⋅sin(0∘)=0
This implies that the magnetic field contribution dB from each segment dl is zero.
Step 7: Conclude the Result
Since the magnetic field contributions from all segments of the wire add up to zero, the total magnetic field B at point X=+a is:
B=0
Final Answer
The magnetic field at the point X=+a due to the straight section PQ is 0.
---
The straight section PQ of the circuit lies along the X-axis from x=−a2 to x=+a2. The current i flows through this section.
We need to calculate the magnetic field at the point X=+a, which is located to the right of the wire segment PQ.
The Biot-Savart law states that the magnetic field dB at a point due to a current element Idl is given by:
dB=μ04πIdl×^rr2
where:
- μ0 is the permeability of free space,
- dl is the current element,
- ^r is the unit vector from the current element to the point where the field is being calculated,
- r is the distance from the current element to the point.
For a small segment dl at position x along the wire, the distance r to the point X=+a is:
r=a−x
The angle θ between dl and ^r can be determined from the geometry of the setup.
Since dl is along the X-axis and ^r points from the wire to the point X=+a, the angle θ between dl and ^r is 0∘ for all points along the wire (since both are along the same line).
Since θ=0∘, we have:
dl×^r=dl⋅sin(0∘)=0
This implies that the magnetic field contribution dB from each segment dl is zero.
Since the magnetic field contributions from all segments of the wire add up to zero, the total magnetic field B at point X=+a is:
B=0
The magnetic field at the point X=+a due to the straight section PQ is 0.
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Circular Arc
69 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Problems Based On Mixed Concepts
32 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Dipole
32 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
Magnetic field at point O due to straight conductor PQ is
_PHY_E06_180_Q01.png)
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View Solution
Knowledge Check
A straight section PQ of a circuit lies along the X-axis from x=−a2 to x=a2 and carriers a steady current i. The magnetic field due to the section PQ at a point X=+a will be
AProportional to aBProportional to a2CProprotional to 1/aDZeroA straight section PQ of a circuit lies along the x-axis from x=−a2 to x=a2 and carries a steady current i. The magnetic field due to the section PQ at a point x =+a will be
Aproportional to aBproportional to a2Cproportional to 1/aDzeroAn element d→l=dxˆi (where dx=1cm) is placed at the origin and carries a large current i=10A. What is the magnetic field on the Y-axis at a distance of 0.5m?
A2×108TB4×108TC6×108TD8×108T
A long straight wire of a circular cross-section (radius r) carries a steady current I. The current is distributed uniformly across the cross-section. Calculare the magnetic field at a point (a) outside the wire , (b) inside the wire. Draw a graph showing variation of magnetic field.
View SolutionA long, straight wire lies along the y-axis and carries a current I=8A in the y-direction (as shown in Fig) In addition to the magnetic field due to the current in the wire, a uniform magnetic field →B0 with magnitude 1.50×10−6T is in the +x direction. What is the total field (magnitude and direction ) at following points in the plane?
(a)x=0,z=1.00m
(b) x=1.00m,z=0
(c) x=0,z=−0.25m

View SolutionA steady current I goes through a wire loop PQR having shape of a right angle triangle with PQ=3x,PR=4xandQR=5x. If the magnitude of the magnetic field at P due to this loop is k(μ0I48πx), find the value of K.
View SolutionA straight thick long wire of uniform cross-section of radius 5cm is carrying a steady current 5A. Calculate the magnetic field at a point 2cm from the axis of wire, well inside the wire.
View Solution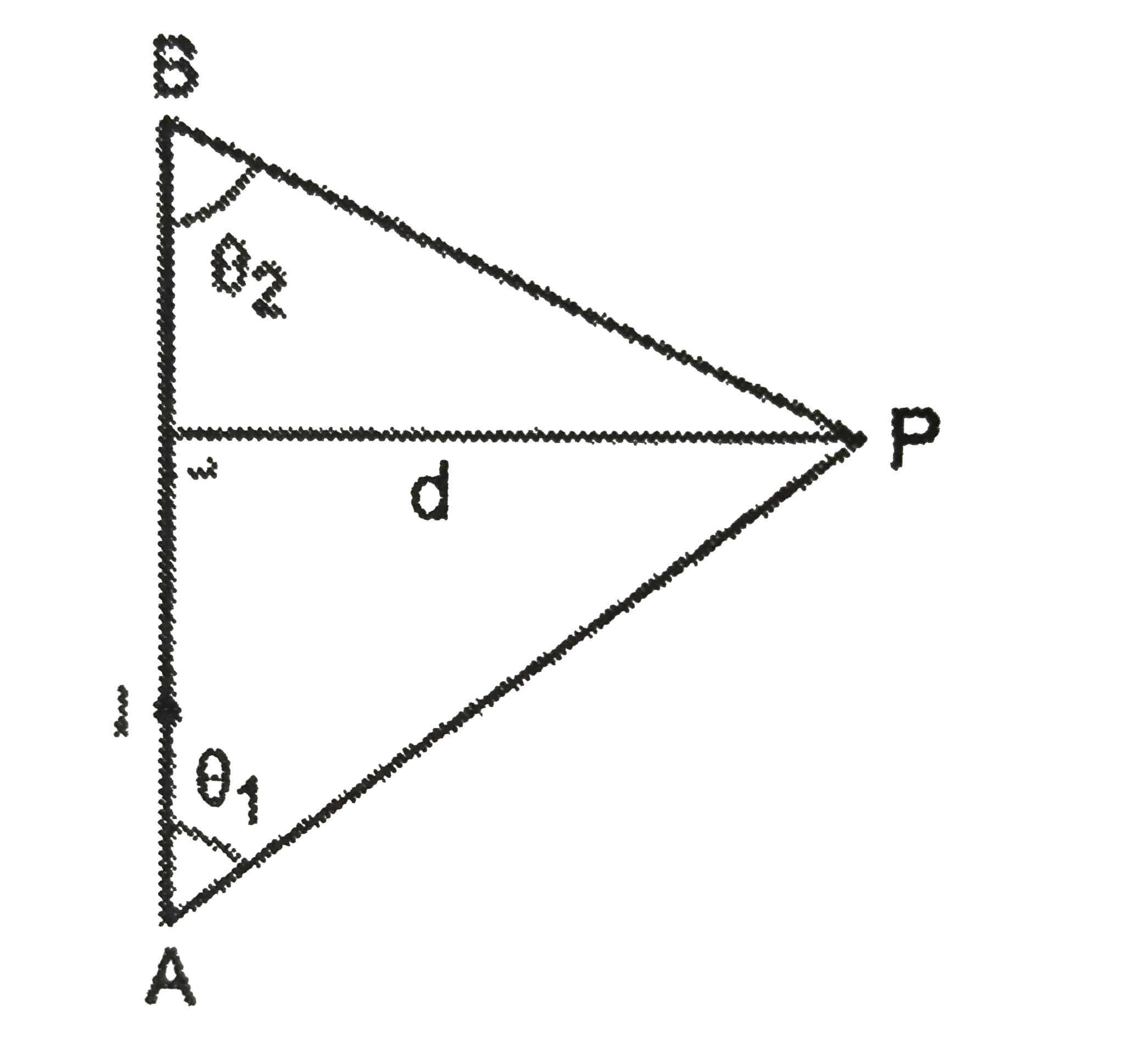
AbB is a section of a straight wire carrying a current I. P is a point at a distance d from AB. The magnetic field at P due to AB has magnitude
View Solution
