Two concentric coplanar circular loops of radii r1 and r2 carry currents of respectively i1 and i2 in opposite direction (one clockwise and the other anticlockwise). The magnetic induction at the centre of the loops is half that due to i1 alone at the centre. if r2=2r1. the value of i2/i1 is
2
1/2
1/4
1
The correct Answer is:D
To solve the problem, we need to find the ratio i2i1 given the conditions of the two concentric circular loops. Let's break down the solution step by step.
Step 1: Understand the Magnetic Field due to a Single Loop
The magnetic field B at the center of a circular loop carrying current i and having radius r is given by the formula:
B=μ0i2r
where μ0 is the permeability of free space.
Step 2: Calculate the Magnetic Field due to Each Loop
For the first loop with radius r1 and current i1:
B1=μ0i12r1
For the second loop with radius r2=2r1 and current i2:
B2=μ0i22r2=μ0i22(2r1)=μ0i24r1
Step 3: Determine the Net Magnetic Field at the Center
Since the currents are in opposite directions, the net magnetic field Bnet at the center of the loops is given by:
Bnet=B1−B2
Substituting the expressions for B1 and B2:
Bnet=μ0i12r1−μ0i24r1
Step 4: Set Up the Equation Based on Given Condition
According to the problem, the net magnetic field at the center is half of the magnetic field due to i1 alone:
Bnet=12B1=12(μ0i12r1)=μ0i14r1
Step 5: Equate the Two Expressions for Bnet
Now we can equate the two expressions for Bnet:
μ0i12r1−μ0i24r1=μ0i14r1
Step 6: Simplify the Equation
Dividing through by μ0 and multiplying by 4r1 to eliminate the fractions:
2i1−i2=i1
This simplifies to:
2i1−i1=i2⇒i2=i1
Step 7: Find the Ratio i2i1
Thus, the ratio of the currents is:
i2i1=i1i1=1
Final Answer
The value of i2i1 is 1.
---
The magnetic field B at the center of a circular loop carrying current i and having radius r is given by the formula:
B=μ0i2r
where μ0 is the permeability of free space.
For the first loop with radius r1 and current i1:
B1=μ0i12r1
B2=μ0i22r2=μ0i22(2r1)=μ0i24r1
Since the currents are in opposite directions, the net magnetic field Bnet at the center of the loops is given by:
Bnet=B1−B2
Substituting the expressions for B1 and B2:
Bnet=μ0i12r1−μ0i24r1
According to the problem, the net magnetic field at the center is half of the magnetic field due to i1 alone:
Bnet=12B1=12(μ0i12r1)=μ0i14r1
Now we can equate the two expressions for Bnet:
μ0i12r1−μ0i24r1=μ0i14r1
Dividing through by μ0 and multiplying by 4r1 to eliminate the fractions:
2i1−i2=i1
This simplifies to:
2i1−i1=i2⇒i2=i1
Thus, the ratio of the currents is:
i2i1=i1i1=1
The value of i2i1 is 1.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Problems Based On Mixed Concepts32videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section B - Assertion Reasoning31videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Current44videos
SOURCE AND EFFECT OF MAGNETIC FIELD
- BOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE29videos
SEMICONDUCTOR ELECTRONICS
- BOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test29videos
WAVE OPTICS
Similar Questions
Two coplanar concentric circular coils of radii r and 2r, have the same number of turns n. The smaller coil carries a clockwise current i, while the larger coil carries an anticlockwise current 2i. The magnetic field induction at the centre is
View SolutionTwo concentric coplanar circular conducting loops have radii R and r(R>>r) .Their mutual inductance is proportional to
View Solution
Knowledge Check
- Question 1 - Select One
Two concentric circular loops of radiir1 and r2 carry clockwise and anticlockwise currents i1 and i2. If the centre is a null point, i1/i2 must be equal to
Ar2/r1Br22/r21Cr21/r22Dr1/r2 - Question 2 - Select One
Two coplanar circular coils of equal radius carrying currents i1,i2 in opposite directions are at a large distance 'd'. The distance from the first coil where the resultant magnetic induction is zero is
Ad1+i2i1Bd1+√i2i1Cd1+(i2i1)13Dd1+(i2i1)2 - Question 3 - Select One
In the figure shown there are two semicircles of radii r1 and r2 in which a current i is flowing. The magnetic induction at the centre O will be
 Aμ0ir(r1+r2)Bμ0i4(r1−r2)Cμ0i4(r1+r2r1r2)Dμ0i4(r1−r2r1r2)
Aμ0ir(r1+r2)Bμ0i4(r1−r2)Cμ0i4(r1+r2r1r2)Dμ0i4(r1−r2r1r2)
Two coaxial circular loops of raadii r1 and r2 are separated by a distance x and carry currents i1 and i2 respectively. Calculate the mutual inductance. What is the force between the loops ?
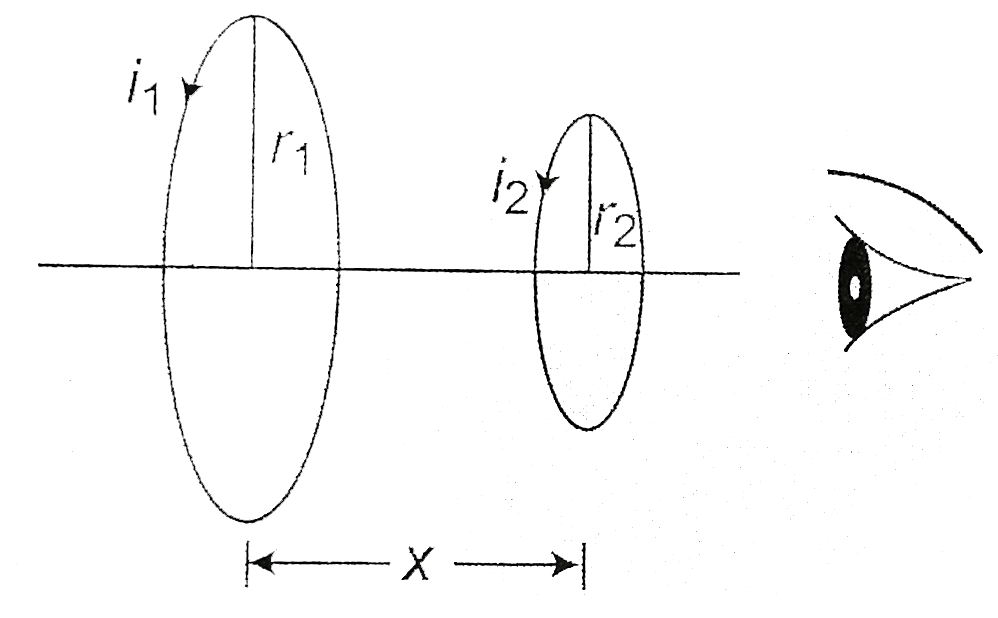 View Solution
View SolutionWhat is the magnetic moment of a circular loop of radius R carrying current I clockwise?
View SolutionTwo wire loop PQRSP formed by joining two semicircular wires of radii R1andR2 carries a current i as shown in the figure given below. What is the magnetic field induction at the centre O in cases (A) and (B) ?
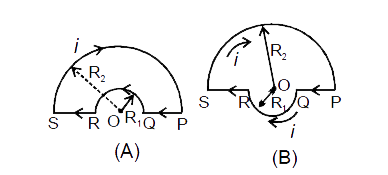 View Solution
View SolutionA circular loop of radius r carries a current i.How should a long, straight wire carrying a current 3i be placed in the plane of the circle so that the magnetic field at the centre of the loop becomes zero?
View SolutionTwo concentric circular coils of radii R and r (<<R) carry currents of i1 and i2 respectively. If the smaller coil is rotated slightly about one of its diameter, it starts oscillating. Then, which of the following statement(s) is/are correct ?
 View Solution
View Solution

