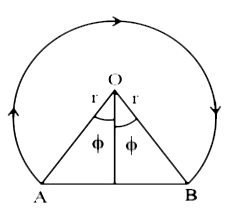
A wire is bent in the form of a circular arc with a straight portion AB. Magnetic induction at O when current flowing in the wire, is

μ02r(π−θ+tanθ)
μ0I2πr(π+θ−tanθ).
μ0I2πr(π−θ+tanθ).
μ0I2πr(−tanθ+π−θ).
The correct Answer is:C
BAB=μ0I4π(OC)[2sinθ]
But OC=rcosθ
or BAB=μ0I2πrtanθ
Magnetic field due to circular portion.
BAB'=μ0I2r2π−2θ2π=μ0I2πr(π−0)
Total magnetic field
=μ0I2πrtanθ+μ0I2πr(π−θ)
=μ0I2πr[tanθ+π−θ]
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Problems Based On Mixed Concepts
32 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Section B - Assertion Reasoning
31 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBOOK - A2ZCHAPTER - SOURCE AND EFFECT OF MAGNETIC FIELDEXERCISE - Magnetic Field Due To Current
44 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - A2ZCHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - EXERCISE
29 Videos
- WAVE OPTICSBOOK - A2ZCHAPTER - WAVE OPTICSEXERCISE - Section D - Chapter End Test
29 Videos
Similar Questions
A wire is bent in the form of a circular arc of radius r with a straight portion AB. If the current in the wire is i, then the magnetic induction at point O is
View SolutionA wire of certain length carries a steady current. It is first bent to form a circular wire of one turn. The same wire is bent to form a circular coil of three turns. The ratio of magnetic induction at the centre of the coil in the two cases is ________
View Solution
Knowledge Check
A long current wire is bent in the shapes shown in figure. The circular portion has radius R. The magnetic induction at the center of the circular segment is
 A−μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],−μ0I4πR[ˆk+ˆj+3π2ˆi]Bμ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]C−μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]Dμ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]
A−μ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],−μ0I4πR[ˆk+ˆj+3π2ˆi]Bμ0I4πR[2ˆkp+πˆi],−μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]C−μ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]Dμ0I4πR[2ˆkp+πˆi],μ0I4πR[ˆk+(π+1)ˆi],μ0I4πR[ˆk+ˆj+3π2ˆi]A current I flows an infinitely long wire with cross section in the form of a semi - circular ring of radius R. The magnitude of the magnetic induction along its axis is :
Aμ0I2π2RBμ0I2πRCμ0I4πRDμ0Iπ2RWhen a certain length of wire is turned into one circular loop, the magnetic induction at the centre of coil due to some current flowing is B1 If the same wire is turned into three loops to make a circular coil, the magnetic induction at the center of this coil for the same current will be
AB1B9B1C3B1D27B1
When a long wire carrying a steady current is best into a circular coil of one turn, the magnetic induction at its centre is B. When the same wire carrying the same current is bent into a circular coil of one turn, the magnetic induction at its centre is B. when the same wire carrying the same current is bent to form a circular coil of a turns of a smaller radius, the magnetic induction at the centre will be
View SolutionA piece of wire carrying a current of 6.00 A is bent in the form of a circular arc of radius 10.0 cm, and it subtends an angle of 120∘ at the centre. Find the magnetic field B due to this piece of wire at the centre.
View SolutionA current I flows in a long straight wire (into the plane of the paper) with cross-section having the from of a circular are of radius R a shown in the figure. Find the magnetic induction at the point O.
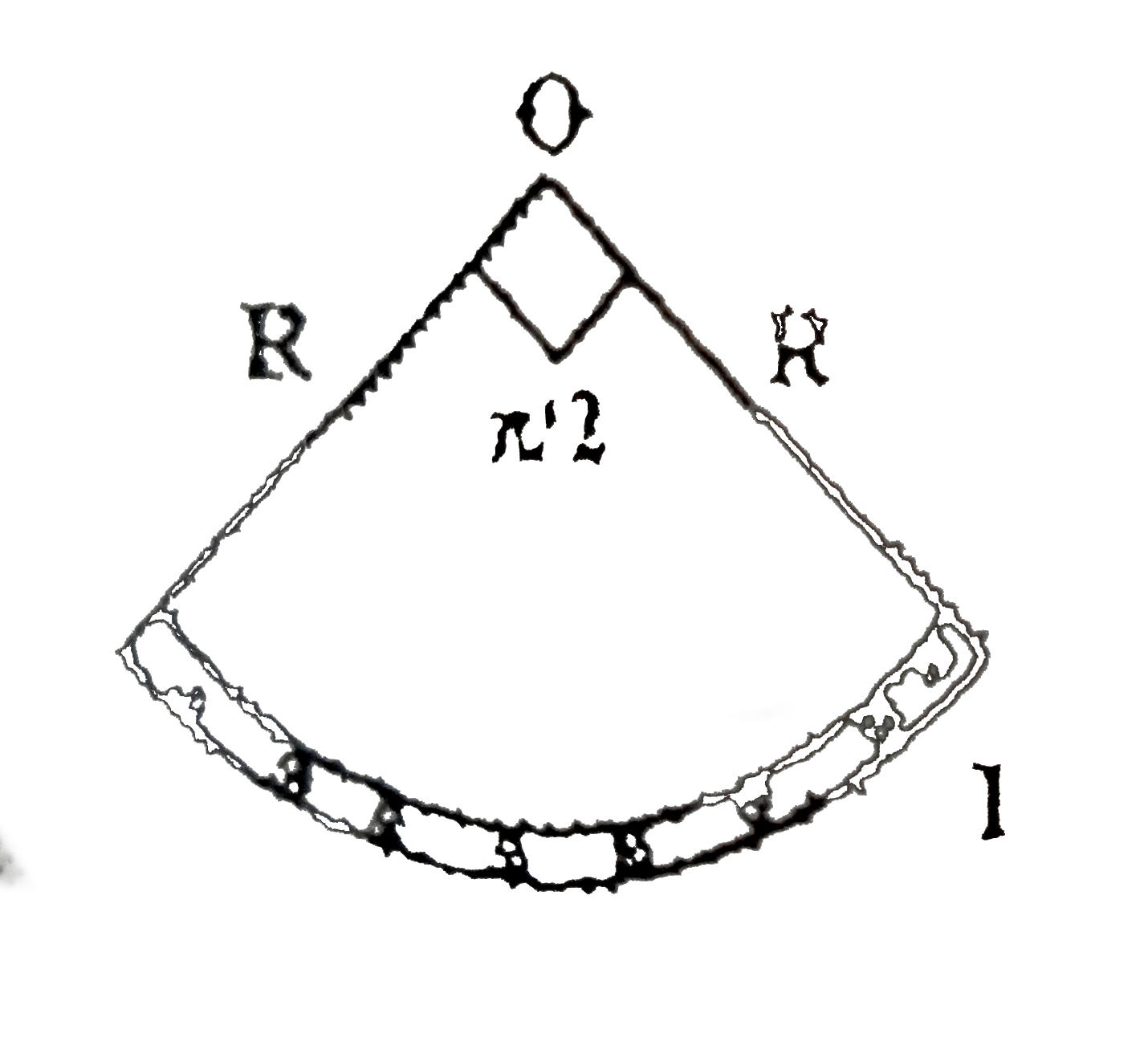
View SolutionA direct current is passing through a wire. It is bent to form a coil of one turn. Now it is further bent to form a coil of two turns but at smaller radius. The ratio of the magnetic induction at the centre of this coils and at the centre of the coil of two turn is
View SolutionA steady current flows in a long wire. It is bent into a circular loop of one turn and the magnetic field at the center of the coil is B. If the same wire is bent into a circular loop of n turns, the magnetic field at the center of the coil is
View Solution
