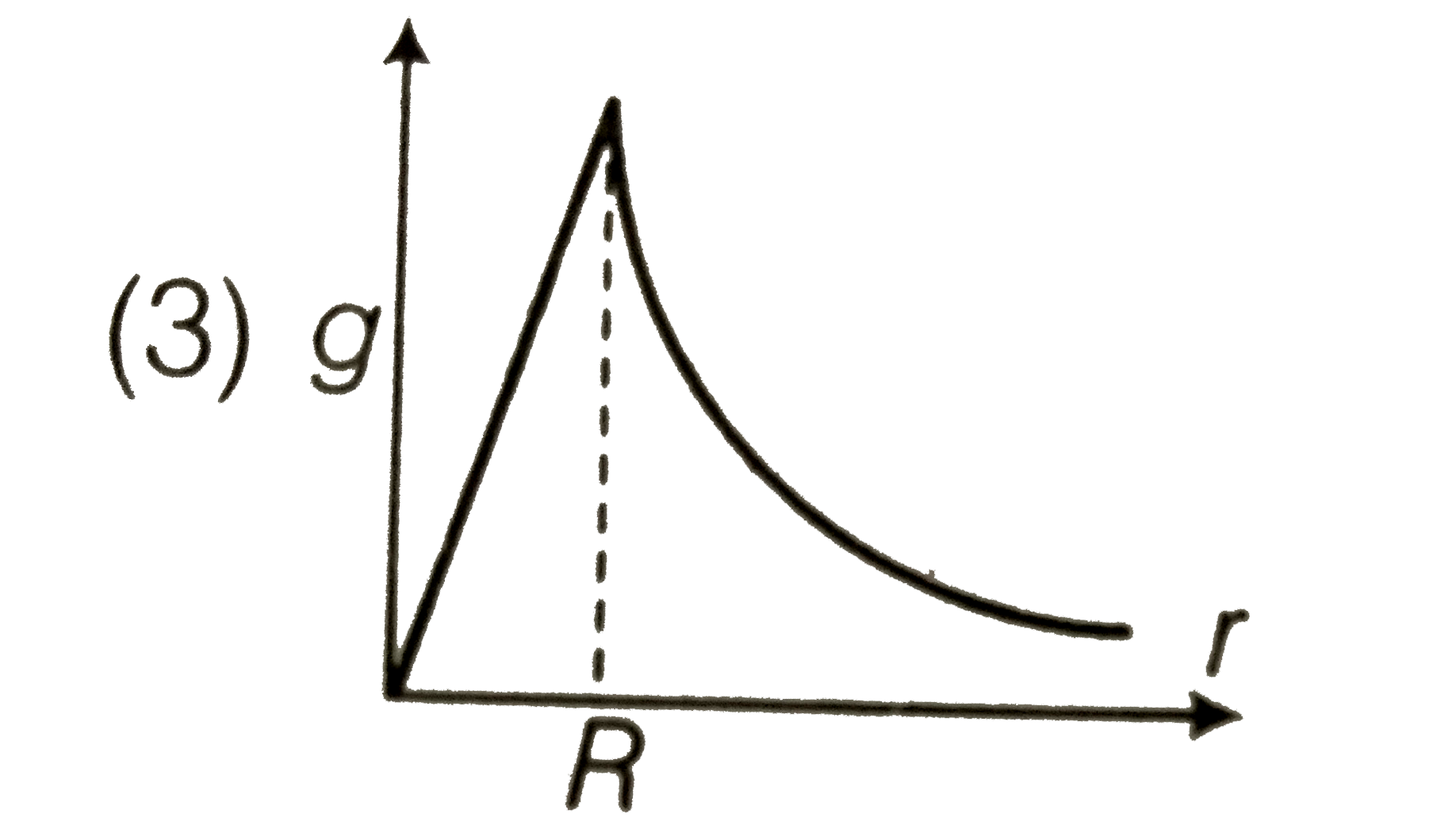
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to br a sphere of radius R of uniform density is as shoen in Fig. below:

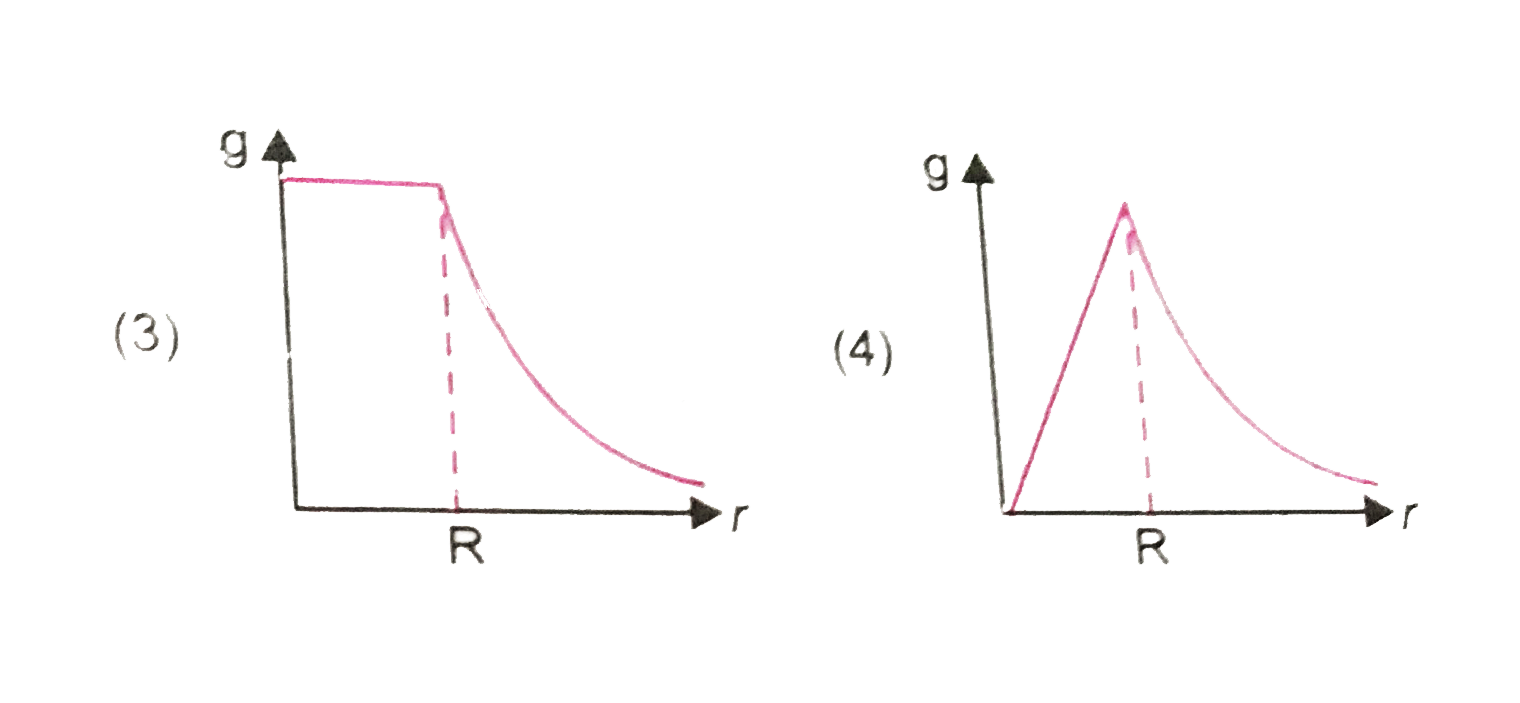
The correct figure is
(4)
(1)
(2)
(3)
The correct Answer is:A
The acceleration due to gravity at a depth d below the surface of earth is
g'=g(1−dR)=g(R−dR)=g(r)R ..(i)
where, R−d=r= distance of location from the centre of the earth. When r=0,g'=0.
From (i) g'∝r, till r=R, for which g'=g
For r>R,g'=gR2(R+h)2=gR2r2 or g'∝1r2
Here R+h=r
Therefore, the variation ofg with distance r from centre of earth will be as shown in figure. Thus, option (a) is correct.
Similar Questions
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be sphere of radius R of uniform density is a shown in figures along side.
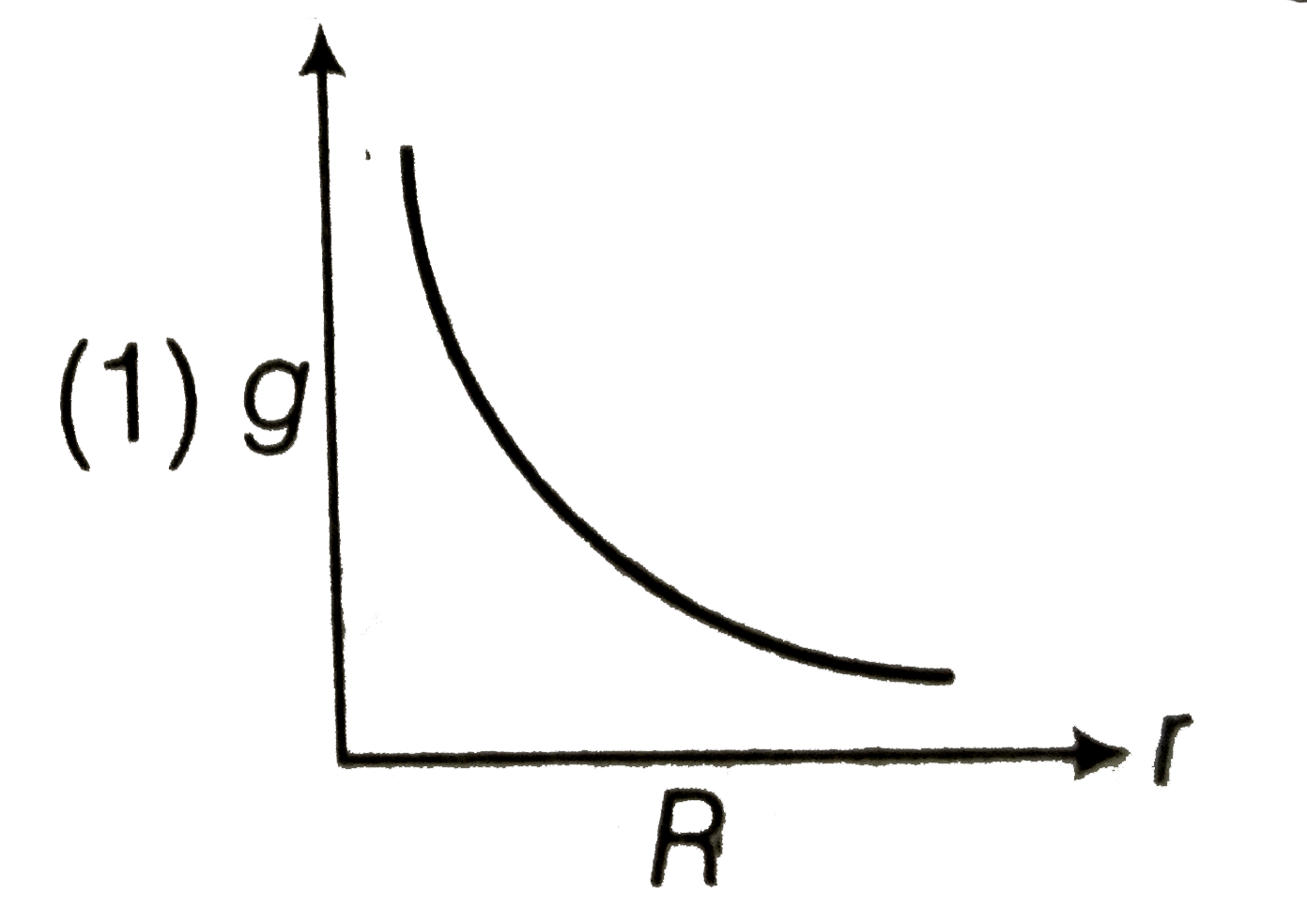
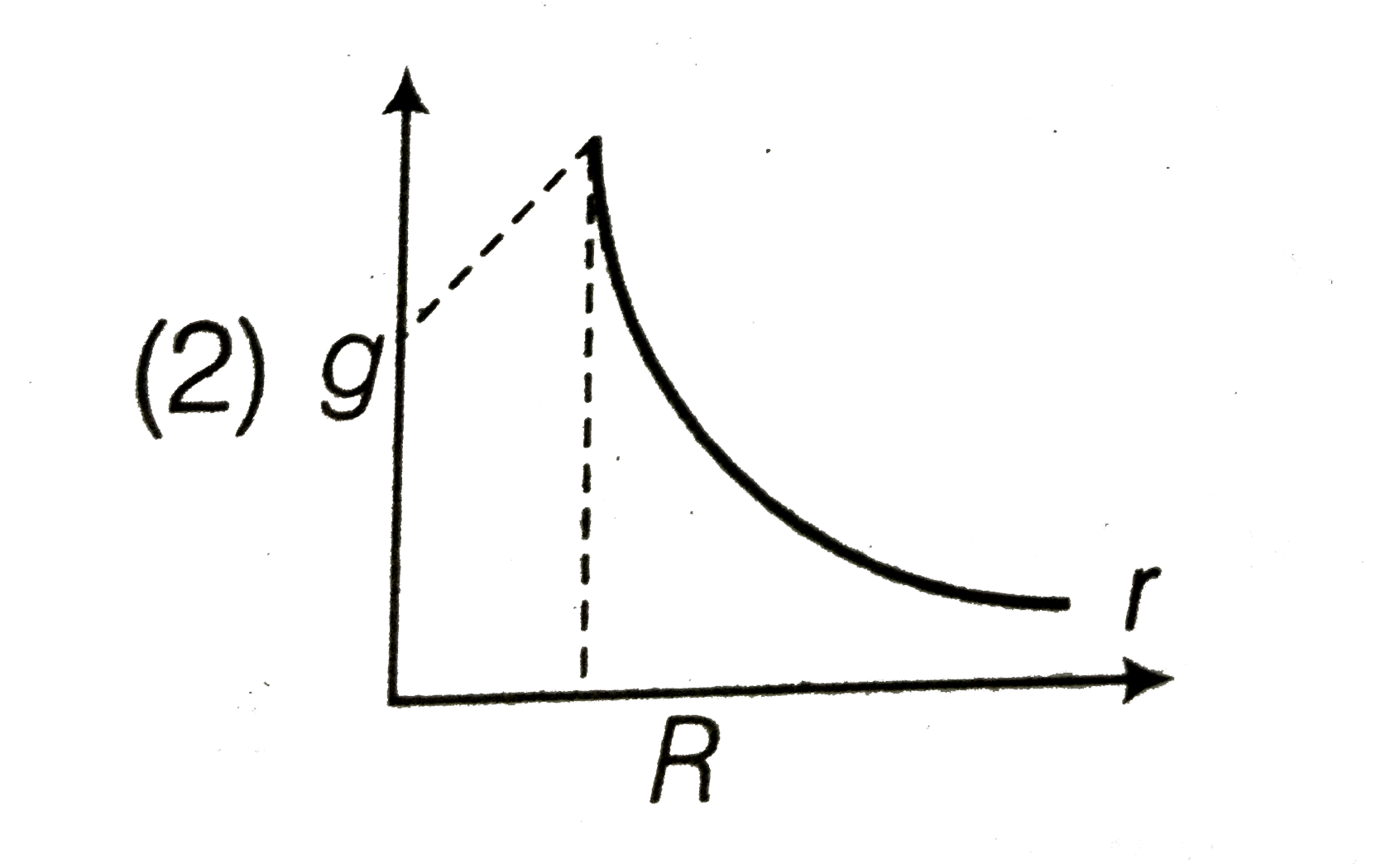
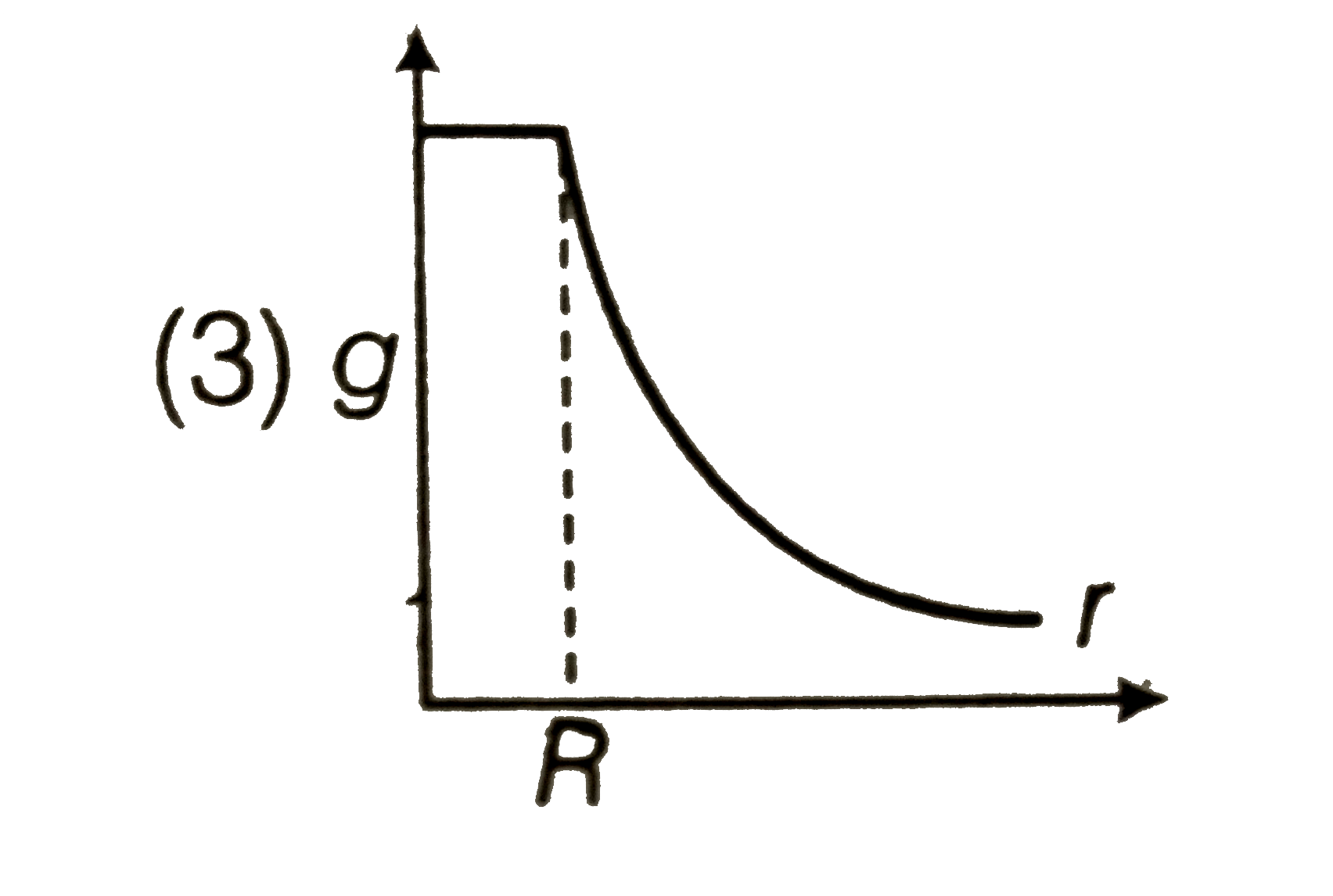
The correct figure isView SolutionFind the acceleration due to gravity at a distance of 20000 kg from the centre of the earth.
View Solution
Knowledge Check
- Question 1 - Select One
Variation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by (R→ Radius of the Earth)
A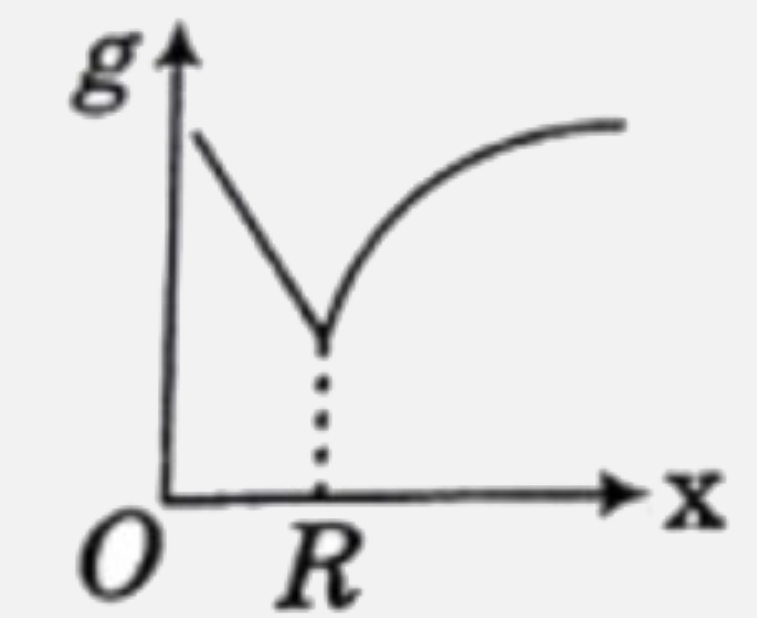 B
B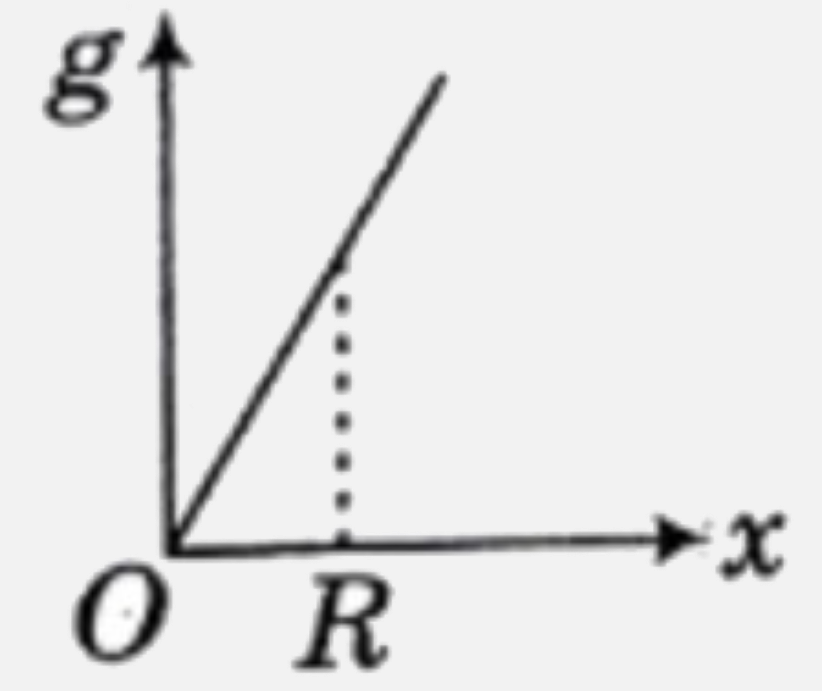 C
C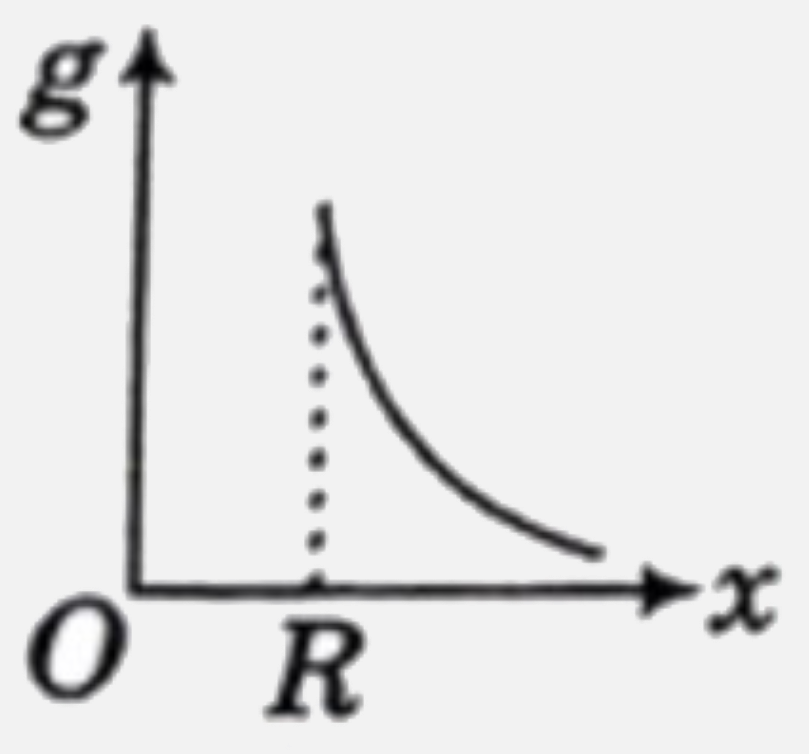 D
D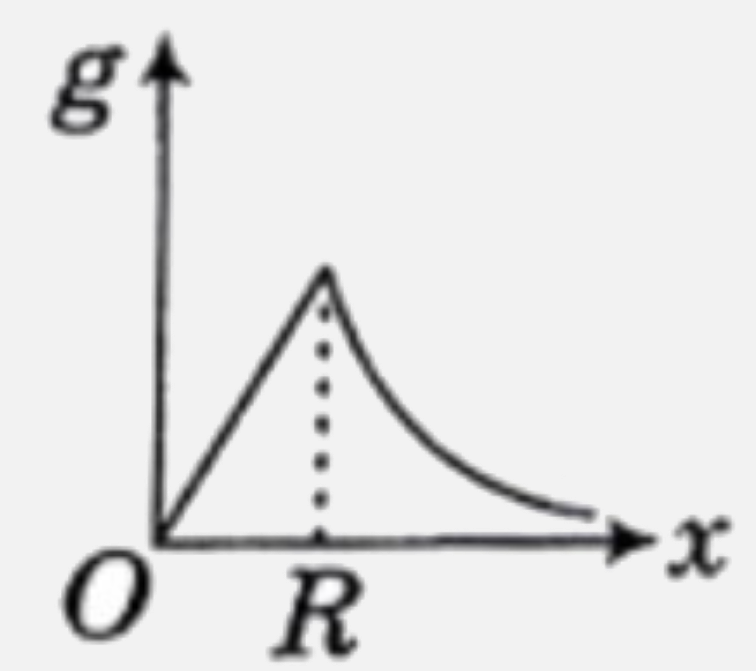
- Question 2 - Select One
The acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
Ag∝rBg∝r2Cg∝r−1Dg∝r−2 - Question 3 - Select One
The acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
A1/rB1/r2CrDr2
Find the acceleration due to gravity at a distance of 20000 km from the centre of the earth.
View SolutionThe acceleration due to gravity at a depth R/2 below the surface of the earth is
View SolutionIf g denotes the value of acceleration due to gravity at a point distance r from the centre of earth of radius R. If r<R, then
View SolutionThe height at which the acceleration due to gravity becomes g/9 in terms of R the radius of the earth is
View SolutionThe value of g (acceleration due to gravity) at earth's surface is 10ms−2. Its value in ms−2 at the centre of the earth which is assumed to be a sphere of radius R metre and uniform mass density is
View Solution

