In car lift compressed air exerts a force F1 on a small piston having a radius of 5 cm. This pressure is transmitted to a second piston of radius 15 cm. If the mass of the car to be lifted is 1350 kg, what is F1? What is the pressure necessary to ac complish this task ?
The correct Answer is:1.47×103N;1.87×105Pa
To solve the problem, we need to find the force F1 exerted by the compressed air on the small piston and the pressure necessary to lift the car.
Step 1: Calculate the weight of the car
The weight F2 of the car can be calculated using the formula:
F2=m⋅g
where:
- m=1350kg (mass of the car)
- g=9.8m/s2 (acceleration due to gravity)
Calculating F2:
F2=1350kg×9.8m/s2=13230N
Step 2: Calculate the areas of the pistons
The area A of a piston is given by the formula:
A=πr2
For the small piston (radius r1=5cm=0.05m):
A1=π(0.05)2=π(0.0025)≈0.00785m2
For the large piston (radius r2=15cm=0.15m):
A2=π(0.15)2=π(0.0225)≈0.07069m2
Step 3: Use Pascal's principle to find F1
According to Pascal's principle, the pressure is the same on both pistons:
F1A1=F2A2
Rearranging the formula to find F1:
F1=F2⋅A1A2
Substituting the values:
F1=13230N⋅0.007850.07069
Calculating F1:
F1≈13230N⋅0.111≈1475.5N
Step 4: Calculate the pressure necessary to lift the car
The pressure P can be calculated using the formula:
P=F1A1
Substituting the values:
P=1475.5N0.00785m2≈187,000Pa or 1.87×105Pa
Final Results
- The force F1 exerted by the compressed air on the small piston is approximately 1475.5N.
- The pressure necessary to lift the car is approximately 1.87×105Pa.
The weight F2 of the car can be calculated using the formula:
F2=m⋅g
where:
- m=1350kg (mass of the car)
- g=9.8m/s2 (acceleration due to gravity)
F2=1350kg×9.8m/s2=13230N
The area A of a piston is given by the formula:
A=πr2
For the small piston (radius r1=5cm=0.05m):
A1=π(0.05)2=π(0.0025)≈0.00785m2
A2=π(0.15)2=π(0.0225)≈0.07069m2
According to Pascal's principle, the pressure is the same on both pistons:
F1A1=F2A2
Rearranging the formula to find F1:
F1=F2⋅A1A2
Substituting the values:
F1=13230N⋅0.007850.07069
Calculating F1:
F1≈13230N⋅0.111≈1475.5N
The pressure P can be calculated using the formula:
P=F1A1
Substituting the values:
P=1475.5N0.00785m2≈187,000Pa or 1.87×105Pa
- The force F1 exerted by the compressed air on the small piston is approximately 1475.5N.
- The pressure necessary to lift the car is approximately 1.87×105Pa.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-II
14 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-I
173 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Fill in the Blanks E
10 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
In a car lift, compressed air exerts a force F1 on a small piston having a radius of 0.5cm. This pressure is transmitted to a second piston of radius 10.0 cm . If the mass of the car to be lifted is 1350 kg. calculate F1. What is the pressure necessary to ac complish this task?
View SolutionIn car lift compressed air exerts a force F1 on a small piston having a radius of 5 cm. This pressure is transmitted to a second piston of radius 15 cm. If the mass of the car to be lifted is 1350 kg, what is F1? What is the pressure necessary to ac complish this task ?
View Solution
Knowledge Check
In a vehicle lifter the enclosed gas exerts a force F on a small piston having a diameter of 8 cm. This pressure is transmitted to a second piston of diameter 24 cm. If the mass of the vehicle to be lifted is 1400 kg then value of F is
A1200 NB1800 NC1600 ND700 NIn a car lift , compressed air with a gauge pressure of 4.0×105 Pa is used to raise a piston with a circular cross-sectional area . If the radius of the piston is 0.17 m , what is the maximum mass that can be raised using this piston ?
A530 kgB3700 kgC9800 kgD22,000 kgIn a hydraulic lift, used at a service station the radius of the large and small piston are in the ration of 20:1. What weight placed on the small piston will be sufficient to lift a car of mass 1500kg ?
A3.75 kgB37.5 kgC7.5 kgD75 kg
If a pressure of 378 atm is exerted on a circular cross section of radius 0.1 mm, what is the force exerted on the area?
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
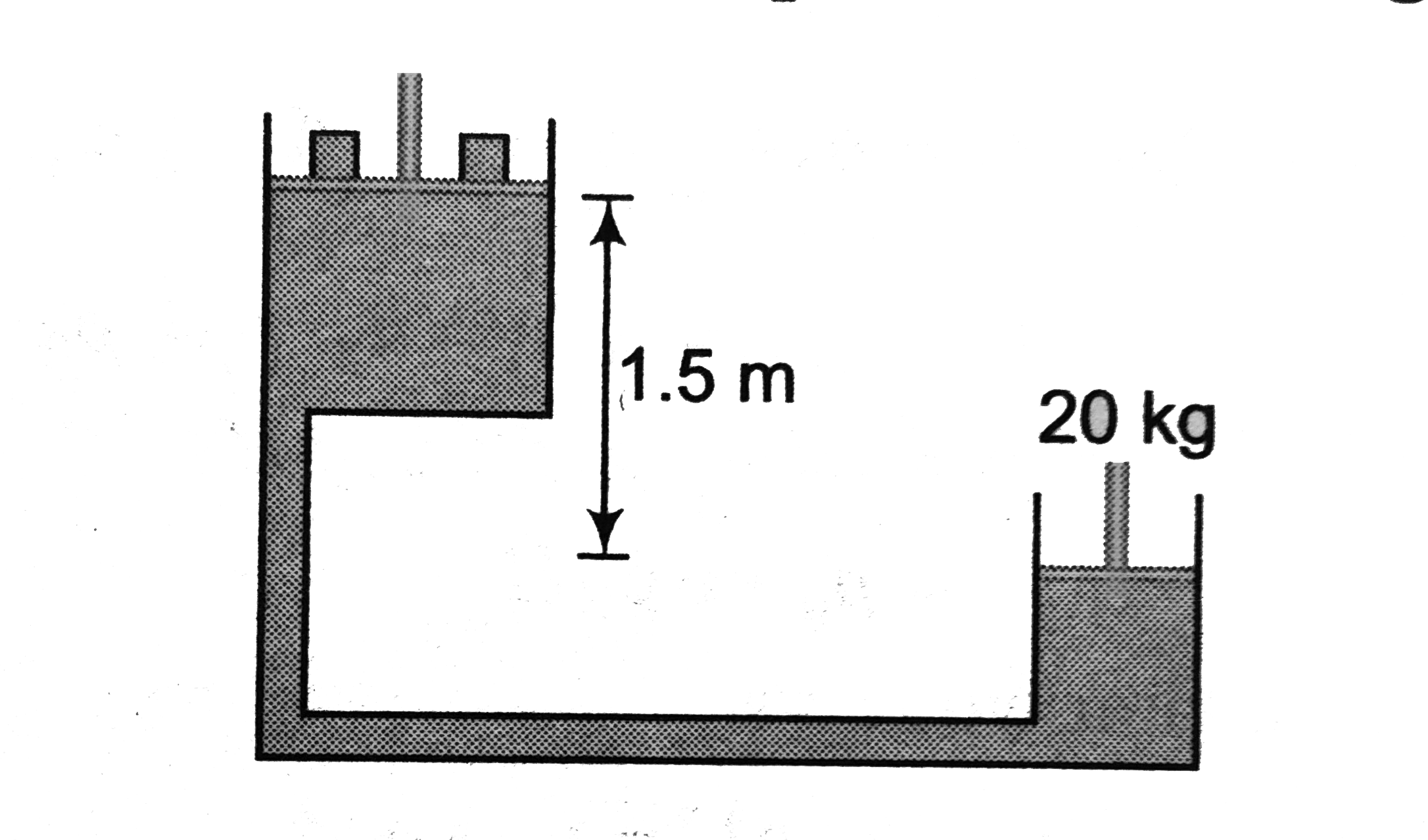 .
.
View SolutionShows a hydraulic press with the larger piston of diameter 35cm at a height of 1.5m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20gk. What is the force exerted on the load by the lerger piston ? The density of oil in the press is 750kgm−3.
View SolutionWhat will be the force required to exert a pressure of 20,000 Pa on an area of 1cm2.
View SolutionThe radius of an air bubble is increasing at the rate of 0.5 cm/sec. At what rate is the volume of the bubble increasing when the radius is 1 cm?
View Solution
