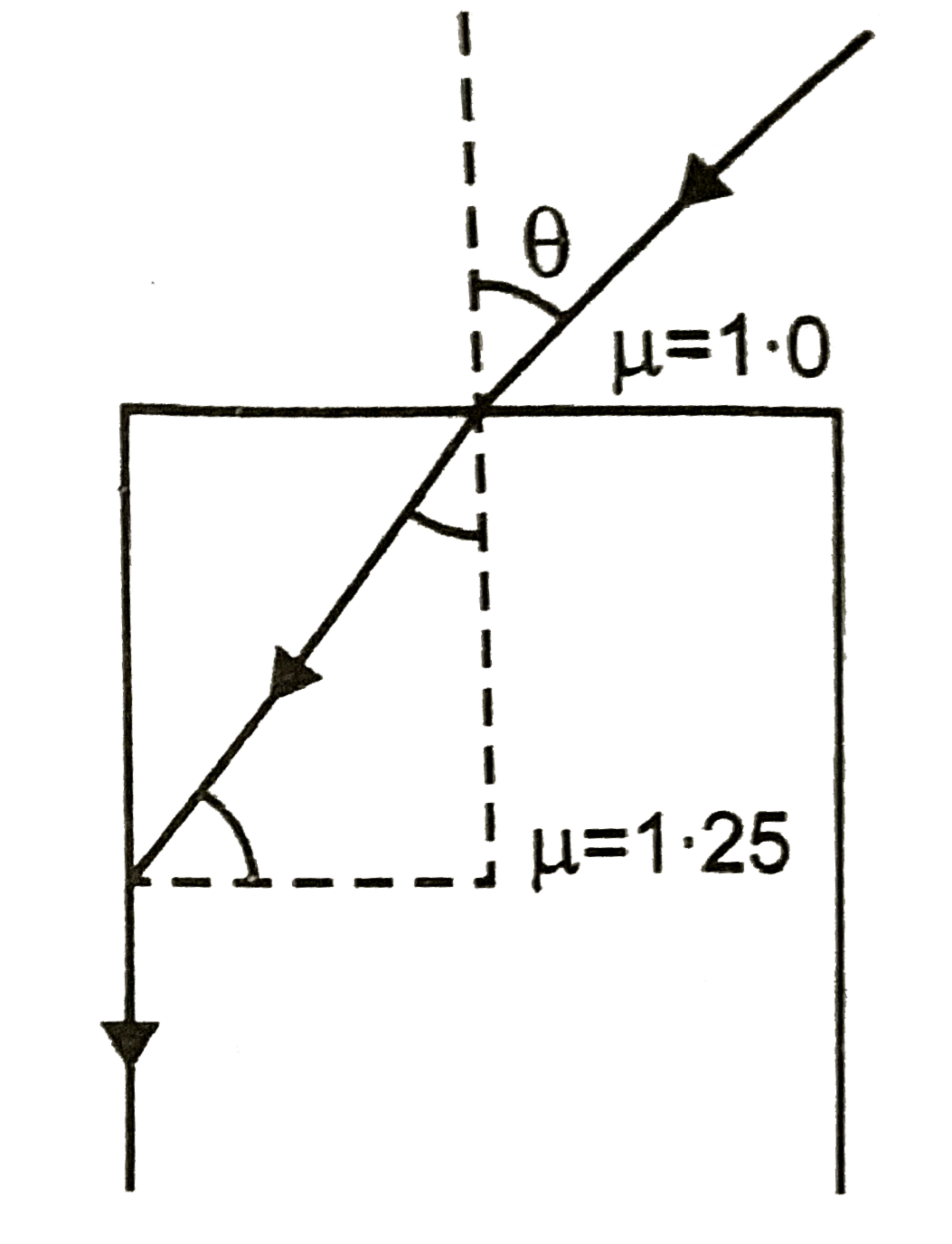
Consider the ray diagram for the refraction given Fig. The maximum value of angle θ for which the light suffers total internal reflection at the vertical surface, is.
 .
.
cos−1(34)
sin−1(34)
tan−1(43)
cot−1(43)
The correct Answer is:B
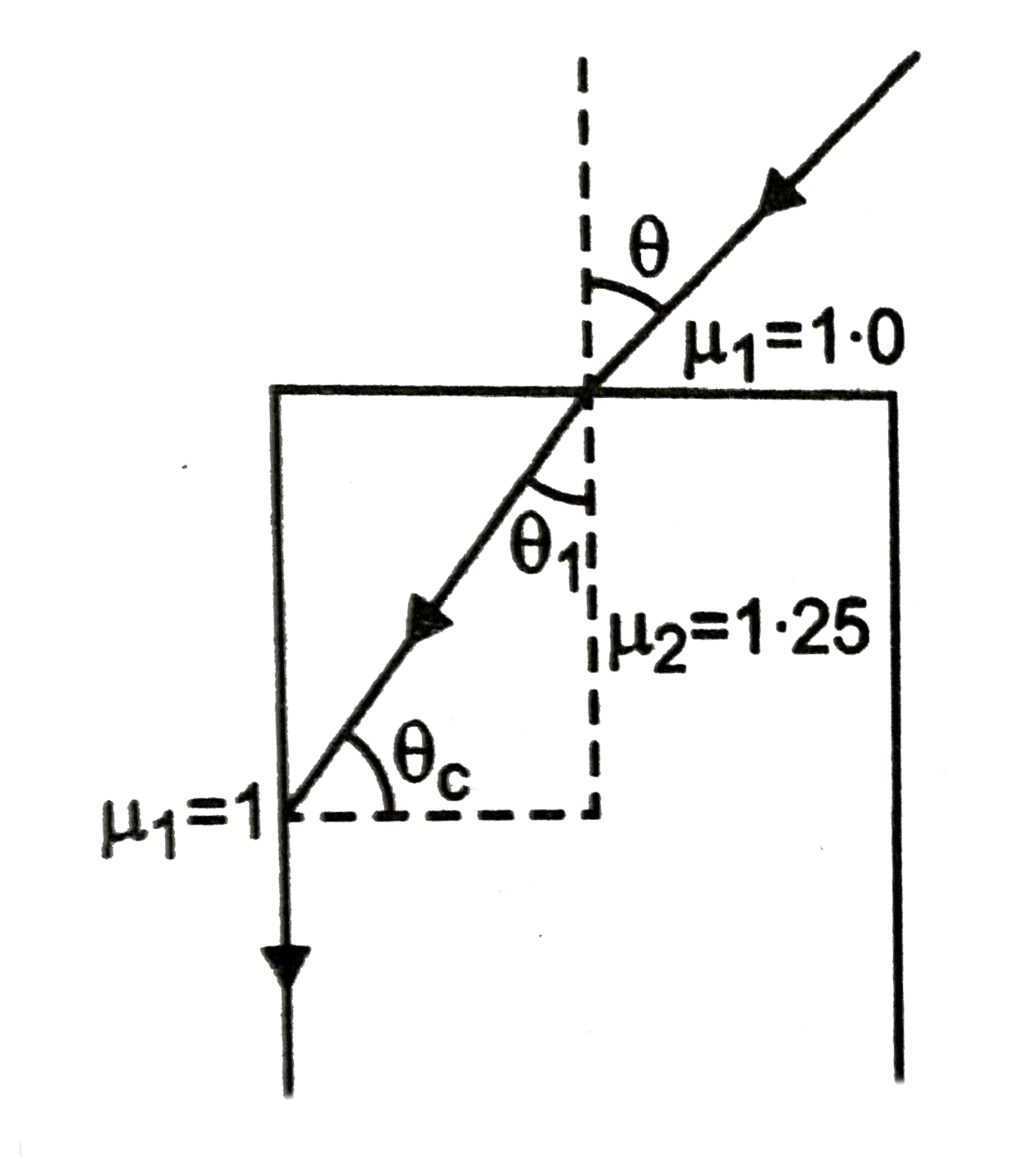
Let the light suffers total internal reflection at the vertical surface where the critical angle is θc as shown in Fig.
sinθc=μ1μ2=11.25=45
Here, θ1=90∘−θc
so sinθ1=sin(90∘−θc)=cosθc=35
For refraction at the horizontal surface
μ2μ1=sinθsinθ1
or 1.251=sinθ3/5
or sinθ=35×1.25=34
or θ=sin−1(3/4).
 .
.
Topper's Solved these Questions
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:(Competition)Comprehension
Explore 7 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Integer Question
Explore 4 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:(Exemplar) Multiple choice
Explore 16 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
Similar Questions
Knowledge Check
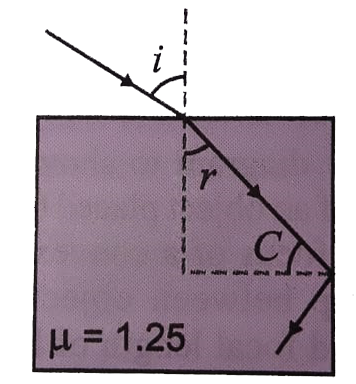
For a situation shown in figure, find the refrective index of glass so that it will suffer total internal reflection at the vertical surface.
 A1.732B1.5C1.31D1.6
A1.732B1.5C1.31D1.6A ray of light is incident on the hypotenuse of a right-angled prism after travelling parallel to the base inside the prism. If μ is the refractive index of the material of the prism, the maximum value of the base angle for which light is totally reflected from the hypotenuse is
Asin−1(Iμ)Btan−1(1μ)Csin−1(μ−1μ)Dcos−1(1μ)
In Fig. find the maximum angle i for which light suffers total internal reflection at the vertical surface.
View SolutionA light rays is incident on a prism of prism angle A and refractive index μ. Show that the smallest value of the angle of incidence for which the reflected ray does not suffer total internal reflection at the second face, i.e. just comes out of it, is given by
i=sin−1[(μ2−1)1/2sinA−cosA].
View SolutionIn the figure shown for an angle of incidence i at the top of the surface, what is the minimum refractive index for total internal reflection at the vertical surface.
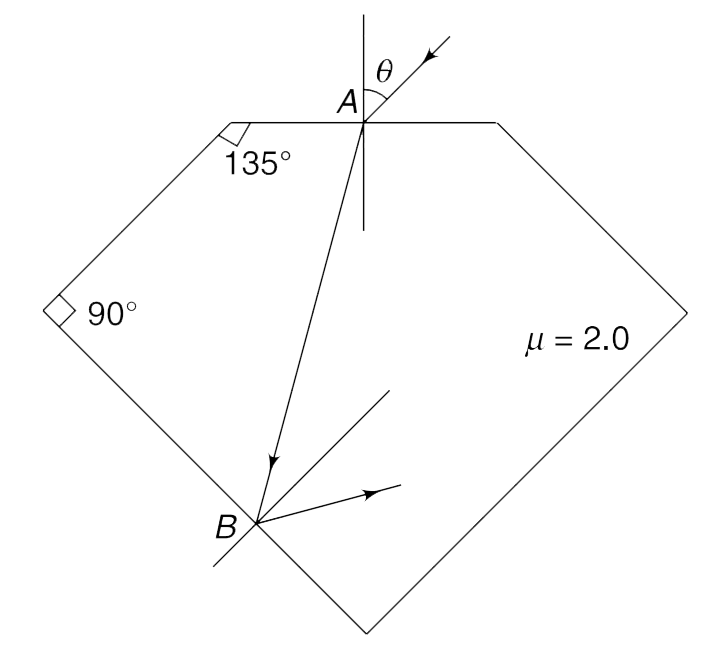
View SolutionLight is incident at point A on one of the faces of a diamond crystal (μ=2.0). Find the maximum allowed value of angle of incidence θ so that light suffers total internal reflection at point B.
View SolutionA slab of refractive index μ is placed in air and light is incident at maximum angle θ0 from vertical. Find minimum value of μ for which total internal reflection takes place at the vertical surface.
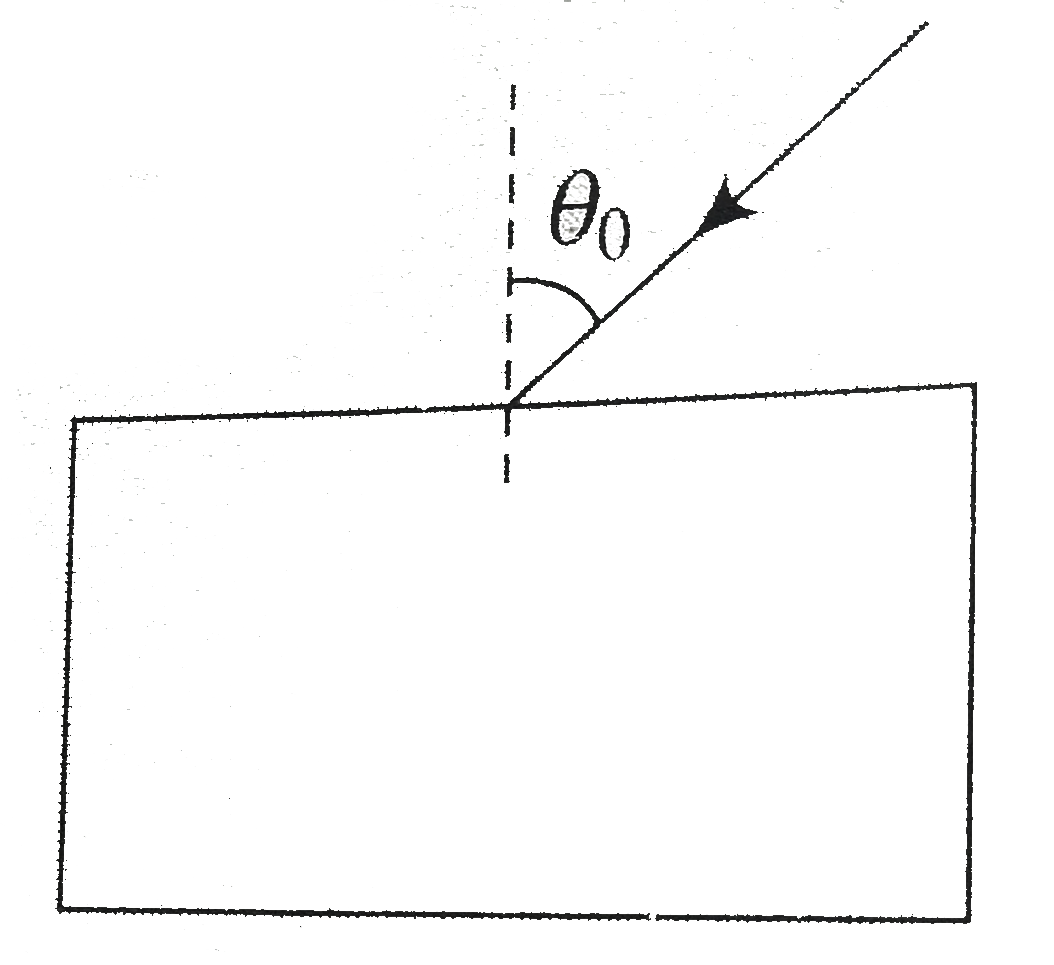
View SolutionA ray of light entering from air into a denser medium of refractive index 43, as shown in figure
The light ray suffers total internal reflection at the adjacent surface as shown. The maximum value of angle θ should be equal to :

View Solution

 .
.