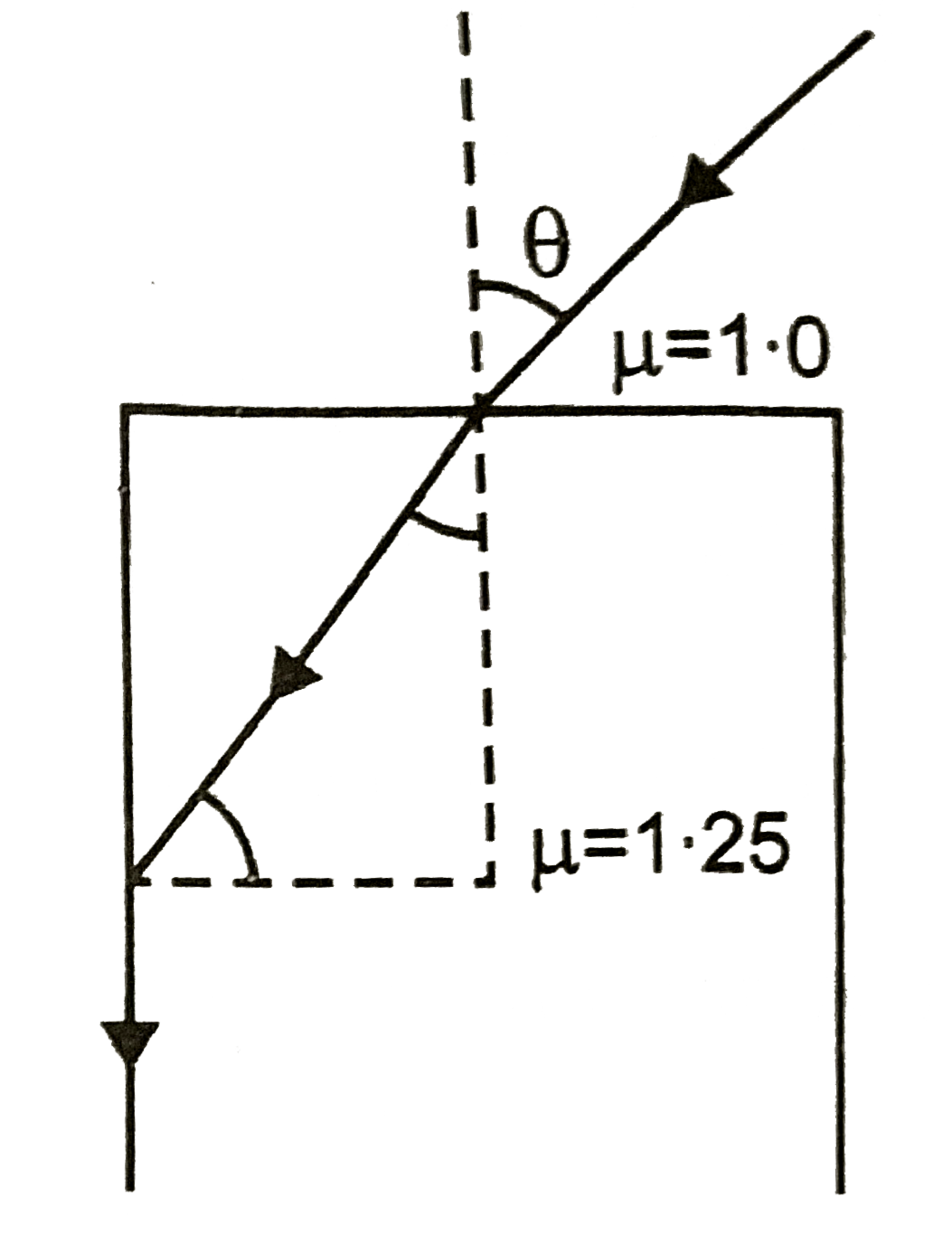
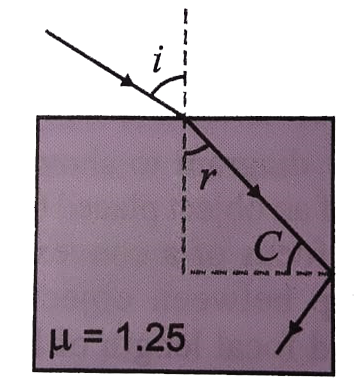
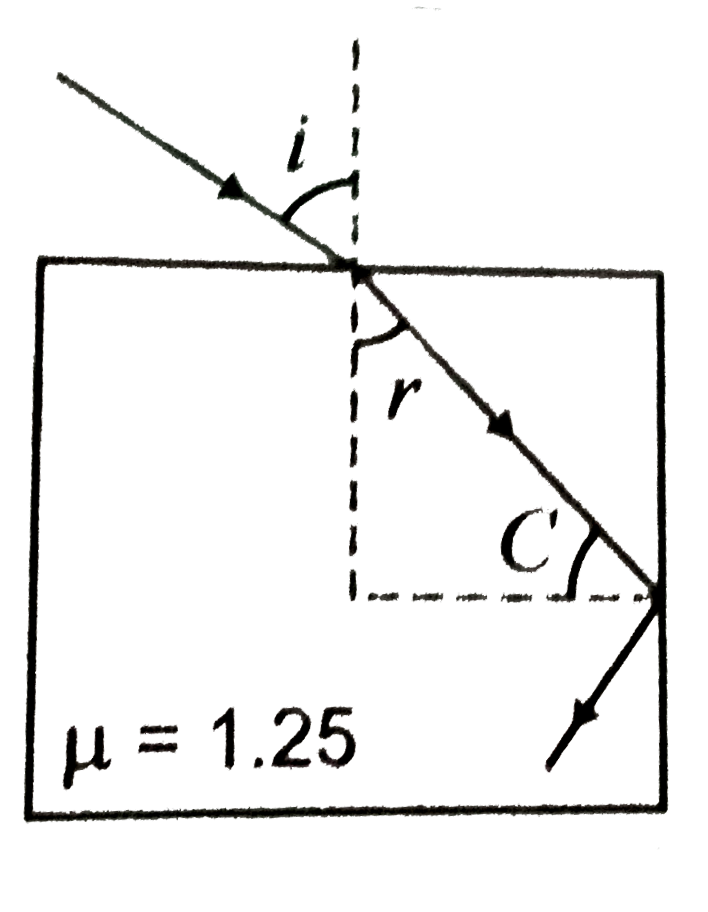
Consider the situation shown in figure. Find the maximum angle theta for which the light suffers total internal reflection at the vertical surface.
To solve the problem of finding the maximum angle θ for which light suffers total internal reflection at the vertical surface, we can follow these steps:
Step 1: Understand the concept of Total Internal Reflection (TIR)
Total Internal Reflection occurs when light attempts to move from a denser medium to a less dense medium, and the angle of incidence exceeds the critical angle. The critical angle can be calculated using the formula:
θc=sin−1(1μ)
where μ is the refractive index of the denser medium relative to the less dense medium.
Step 2: Identify the refractive index
In this problem, the refractive index μ is given as 1.25. This means that light is moving from a medium with a refractive index of 1.25 to air (which has a refractive index of approximately 1).
Step 3: Calculate the critical angle
Using the formula for the critical angle:
θc=sin−1(11.25)
Calculating this gives:
θc=sin−1(0.8)
Using a calculator or trigonometric tables, we find:
θc≈53.13∘
Step 4: Relate the critical angle to the angle θ
For total internal reflection to occur at the vertical surface, the angle θ must be related to the critical angle. The angle θ can be determined using the relationship:
θ=90∘−θc
Substituting the value of θc:
θ=90∘−53.13∘≈36.87∘
Step 5: Conclusion
Thus, the maximum angle θ for which light suffers total internal reflection at the vertical surface is approximately:
θ≈36.87∘
Total Internal Reflection occurs when light attempts to move from a denser medium to a less dense medium, and the angle of incidence exceeds the critical angle. The critical angle can be calculated using the formula:
θc=sin−1(1μ)
where μ is the refractive index of the denser medium relative to the less dense medium.
In this problem, the refractive index μ is given as 1.25. This means that light is moving from a medium with a refractive index of 1.25 to air (which has a refractive index of approximately 1).
Using the formula for the critical angle:
θc=sin−1(11.25)
Calculating this gives:
θc=sin−1(0.8)
Using a calculator or trigonometric tables, we find:
θc≈53.13∘
For total internal reflection to occur at the vertical surface, the angle θ must be related to the critical angle. The angle θ can be determined using the relationship:
θ=90∘−θc
Substituting the value of θc:
θ=90∘−53.13∘≈36.87∘
Thus, the maximum angle θ for which light suffers total internal reflection at the vertical surface is approximately:
θ≈36.87∘
Similar Questions
Knowledge Check
Consider the ray diagram for the refraction given Fig. The maximum value of angle θ for which the light suffers total internal reflection at the vertical surface, is.
 .Acos−1(34)Bsin−1(34)Ctan−1(43)Dcot−1(43)
.Acos−1(34)Bsin−1(34)Ctan−1(43)Dcot−1(43)Consider the ray diagram for the refraction given Fig. The maximum value of angle θ for which the light suffers total internal reflection at the vertical surface, is
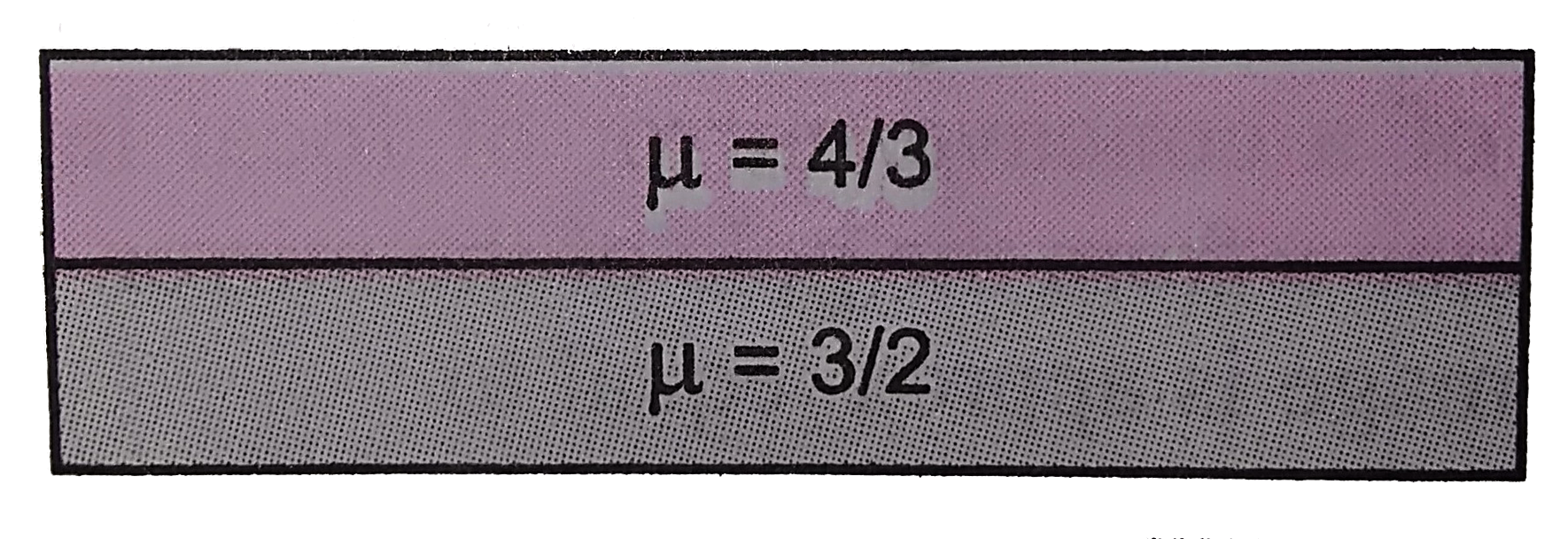 Acos−1(34)Bsin−1(34)Ctan−1(34)Dcot−1(34)
Acos−1(34)Bsin−1(34)Ctan−1(34)Dcot−1(34)For a situation shown in figure, find the refrective index of glass so that it will suffer total internal reflection at the vertical surface.
 A1.732B1.5C1.31D1.6
A1.732B1.5C1.31D1.6
Total internal reflection and critical angle
View SolutionDefine total internal reflection of light.
View SolutionConsider the situation shown in the figure.
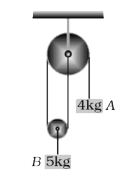
Find acceleration of A.
View SolutionConsider the situation shown in the figure.
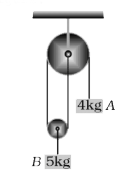
Find acceleration of B.
View SolutionFor total internal reflection, light must travel
View Solution

 .
.