A uniform conducting wire of length and resistance R is wound up as a current carrying coil in the shape of (i) an equilateral triangle of side a, (ii) a square of sides a and, (iii) a regular hexagon of sides a. The coil is connected to a voltage source . Find the magnetic moment of the coils in each case.
To find the magnetic moment of the coils in each case, we will follow these steps:
Step 1: Determine the Current (I) in the Coil
The current flowing through the coil can be calculated using Ohm's law:
I=V0R
where V0 is the voltage of the source and R is the resistance of the wire.
Step 2: Find the Number of Turns (N)
The total length of the wire is given as 12a. The perimeter of each shape will determine how many turns can be made.
1. Equilateral Triangle:
- Perimeter = 3a
- Number of turns, N=12a3a=4
2. Square:
- Perimeter = 4a
- Number of turns, N=12a4a=3
3. Regular Hexagon:
- Perimeter = 6a
- Number of turns, N=12a6a=2
Step 3: Calculate the Area (A) of Each Shape
1. Equilateral Triangle:
- Area A=√34a2
2. Square:
- Area A=a2
3. Regular Hexagon:
- Area A=3√32a2
Step 4: Calculate the Magnetic Moment (M)
The magnetic moment M is given by the formula:
M=NIA
Now we can calculate the magnetic moment for each shape.
1. Equilateral Triangle:
M=NIA=4⋅(V0R)⋅(√34a2)=V0√3a2R
2. Square:
M=NIA=3⋅(V0R)⋅(a2)=3V0a2R
3. Regular Hexagon:
M=NIA=2⋅(V0R)⋅(3√32a2)=3√3V0a2R
Final Results
- Equilateral Triangle: M=V0√3a2R
- Square: M=3V0a2R
- Regular Hexagon: M=3√3V0a2R
The current flowing through the coil can be calculated using Ohm's law:
I=V0R
where V0 is the voltage of the source and R is the resistance of the wire.
The total length of the wire is given as 12a. The perimeter of each shape will determine how many turns can be made.
- Perimeter = 3a
- Number of turns, N=12a3a=4
- Perimeter = 4a
- Number of turns, N=12a4a=3
- Perimeter = 6a
- Number of turns, N=12a6a=2
1. Equilateral Triangle:
- Area A=√34a2
- Area A=a2
- Area A=3√32a2
The magnetic moment M is given by the formula:
M=NIA
M=NIA=4⋅(V0R)⋅(√34a2)=V0√3a2R
M=NIA=3⋅(V0R)⋅(a2)=3V0a2R
M=NIA=2⋅(V0R)⋅(3√32a2)=3√3V0a2R
- Equilateral Triangle: M=V0√3a2R
- Square: M=3V0a2R
- Regular Hexagon: M=3√3V0a2R
Topper's Solved these Questions
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Conceptual Problems (d)
2 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Very Short Answer Questions (a)
2 Videos
- ELECTROSTATICSBOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS
2 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Multiple choice questions
1 Videos
Similar Questions
A uniform conducting wire of length 12a and resistance 'R' is wound up as a current carrying coil in the shape of
1. an equilateral triangle of side 'a'
2. a square of side 'a'
The magnetic dipole moments of the coil in each case resp. are.
View SolutionA uniform conducting wire of length 18a and resistance R is wound up as current carrying coil in the shape of a regular a hexagon of sides a. If the coil is connected to a voltage source V0, then the magnetic moment of coil is

View Solution
Knowledge Check
A regular hexagone of side a. A wire of length 24 a is coiled on that hexagone. If current in hexagone is I, then find the magnetic moment.
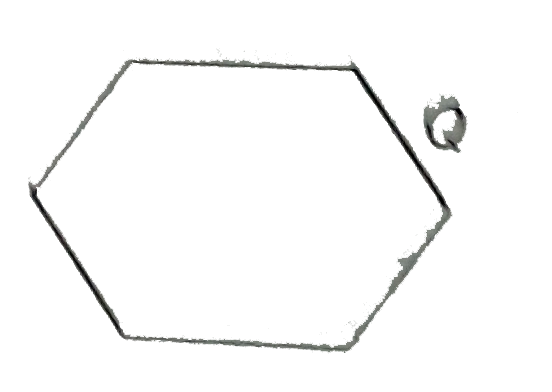 A6√3la2B3√3la2C3√32la2D6la2
A6√3la2B3√3la2C3√32la2D6la2A current I is flowing in a hexgonal coil of side a figure. The magnetic field induction at the centre O of the coil will be
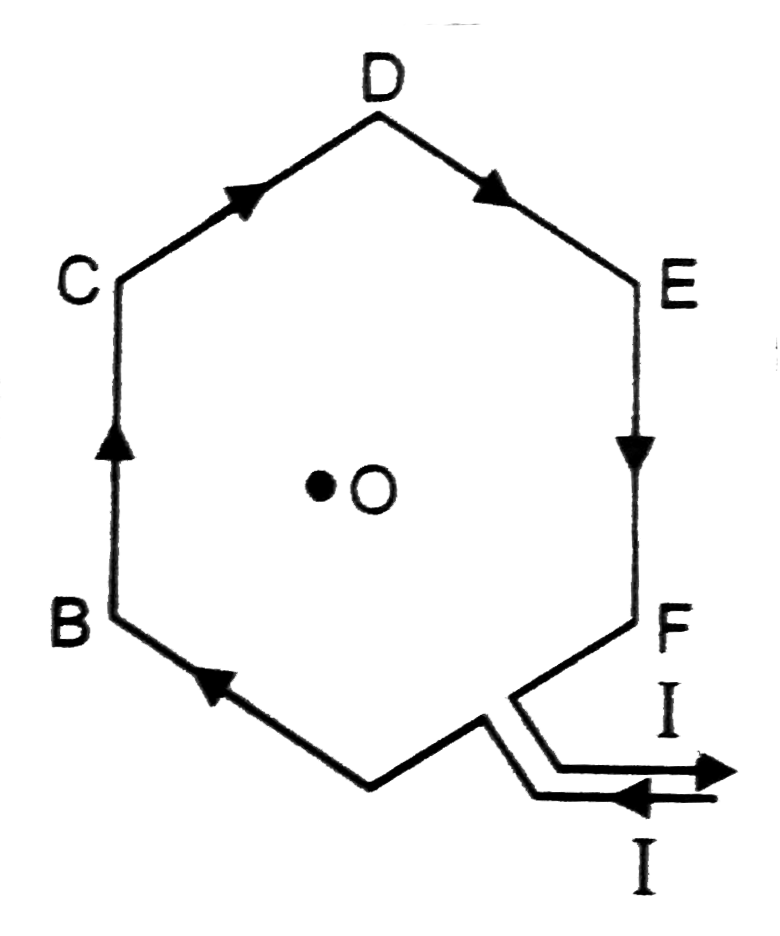 A√2μ0IπaB√3μ0IπaC2πa√3IDμ0Iπa
A√2μ0IπaB√3μ0IπaC2πa√3IDμ0Iπa
A uniform conducting wire of length length 10a and resistance R is wound up into four turn as a current carrying coil in the shape of equilateral triangle of side a. If current I is flowing 4 through the coil then the magnetic moment of the coil is
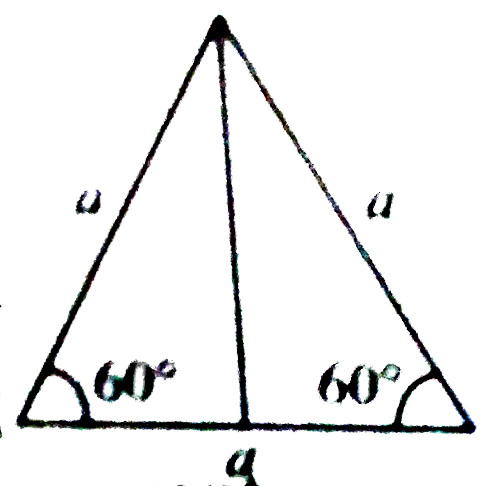
View SolutionA square loop of side l carries a current i. it is placed as shown in figure. Find the magnetic moment of the loop.
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionA loop in the shape of an equilateral triangle triangle of side a carries a current I as shown in the figure.Find out the magnetic field at the centre C of the triangle.

View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.

View SolutionAn equilateral triangle of side length l is formed from a piece of wire of uniform resistance. The current I is as shown in figure. Find the magnitude of the magnetic field at its centre O.

View Solution
