A uniform conducting wire of length 12a and resistance 'R' is wound up as a current carrying coil in the shape of
1. an equilateral triangle of side 'a'
2. a square of side 'a'
The magnetic dipole moments of the coil in each case resp. are.
3Ia2 and 4Ia2
4Ia2 and 3Ia2
√3Ia2 and 3Ia2
3Ia2 and Ia2
To solve the problem, we need to calculate the magnetic dipole moments of a coil formed by a uniform conducting wire of length 12a and resistance R, wound in two different shapes: an equilateral triangle and a square, both with side length 'a'.
1. Determine the number of turns for the equilateral triangle:
- The perimeter of an equilateral triangle with side 'a' is given by:
Ptriangle=3a
- The total length of the wire is 12a. Therefore, the number of turns (N1) that can be made is:
N1=Total Length of WirePerimeter of Triangle=12a3a=4
2. Calculate the area of the equilateral triangle:
- The area (A1) of an equilateral triangle with side 'a' is given by:
A1=√34a2
3. Calculate the magnetic dipole moment for the equilateral triangle:
- The magnetic dipole moment (M1) is given by:
M1=N1⋅I⋅A1
- Substituting the values:
M1=4⋅I⋅(√34a2)=√3Ia2
4. Determine the number of turns for the square:
- The perimeter of a square with side 'a' is given by:
Psquare=4a
- The number of turns (N2) that can be made is:
N2=Total Length of WirePerimeter of Square=12a4a=3
5. Calculate the area of the square:
- The area (A2) of a square with side 'a' is given by:
A2=a2
6. Calculate the magnetic dipole moment for the square:
- The magnetic dipole moment (M2) is given by:
M2=N2⋅I⋅A2
- Substituting the values:
M2=3⋅I⋅a2=3Ia2
Final Results:
- The magnetic dipole moment for the equilateral triangle is:
M1=√3Ia2
- The magnetic dipole moment for the square is:
M2=3Ia2
- The perimeter of an equilateral triangle with side 'a' is given by:
Ptriangle=3a
- The total length of the wire is 12a. Therefore, the number of turns (N1) that can be made is:
N1=Total Length of WirePerimeter of Triangle=12a3a=4
- The area (A1) of an equilateral triangle with side 'a' is given by:
A1=√34a2
- The magnetic dipole moment (M1) is given by:
M1=N1⋅I⋅A1
- Substituting the values:
M1=4⋅I⋅(√34a2)=√3Ia2
- The perimeter of a square with side 'a' is given by:
Psquare=4a
- The number of turns (N2) that can be made is:
N2=Total Length of WirePerimeter of Square=12a4a=3
- The area (A2) of a square with side 'a' is given by:
A2=a2
- The magnetic dipole moment (M2) is given by:
M2=N2⋅I⋅A2
- Substituting the values:
M2=3⋅I⋅a2=3Ia2
- The magnetic dipole moment for the equilateral triangle is:
M1=√3Ia2
- The magnetic dipole moment for the square is:
M2=3Ia2
Topper's Solved these Questions
Similar Questions
A uniform conducting wire of length 12a and resistance R is wound up as a current carrying coil in the shape of (i) an equilateral triangle of side a, (ii) a square of sides a and, (iii) a regular hexagon of sides a. The coil is connected to a voltage source V0. Find the magnetic moment of the coils in each case.
View SolutionA uniform conducting wire of length length 10a and resistance R is wound up into four turn as a current carrying coil in the shape of equilateral triangle of side a. If current I is flowing 4 through the coil then the magnetic moment of the coil is
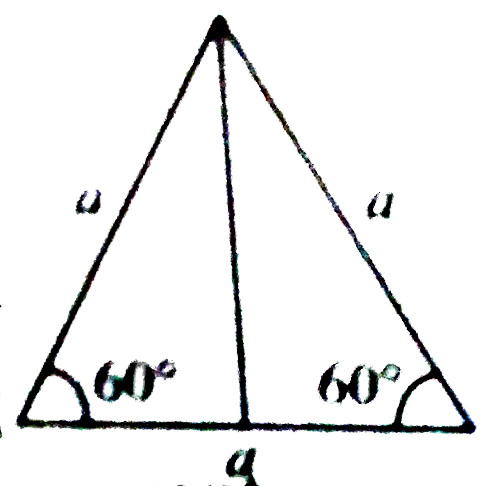
View Solution
Knowledge Check
A current of 10A is flowing in a equilateral triangle of side length l=1M as shown in figure. The magnetic field at center of triangle is:
_2019_CBT6_E01_040_Q01.png) A8×10−6TB9×10−5TC9×10−6TD10−5T
A8×10−6TB9×10−5TC9×10−6TD10−5TA magnet of length 10cm and magnetic moment 1Am2 is placed along the side of an equilateral triangle of the side AB of length 10cm. The magnetic induction at third vetex C is
A10−9TB10−7C10−5TD10−4TA circular coil of diameter 9 cm has 30 turns of wire which carry current of 1 ampere. The magnetic moment of the coil is
A19.08×10−2Am2B3.8×10−2Am2C7.7×10−3Am2D3.8×10−3Am2
A uniform conducting wire of length 18a and resistance R is wound up as current carrying coil in the shape of a regular a hexagon of sides a. If the coil is connected to a voltage source V0, then the magnetic moment of coil is

View SolutionMagnetic field at center of an equilateral triangle of side length 9cm having current 2A is
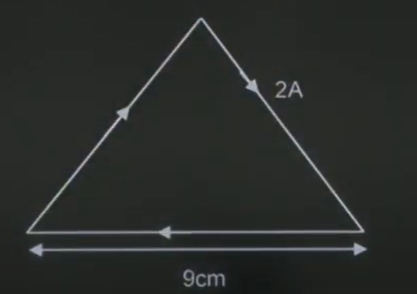
View SolutionA wire shaped to a regular hexagon of side 2cm carries a current of 2A. Find the magnetic field at the cetre of the hexagon.
View SolutionA loop in the shape of an equilateral triangle triangle of side a carries a current I as shown in the figure.Find out the magnetic field at the centre C of the triangle.

View SolutionOne side of an equilateral triangle is 3x+4y=7 and its vertex is (1,2). Then the length of the side of the triangle is
View Solution
