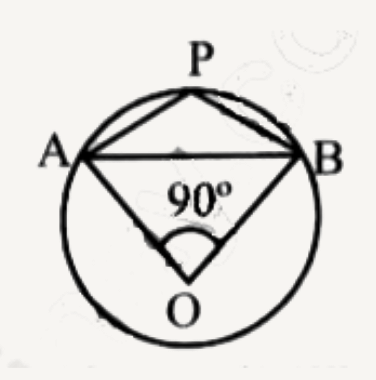
In the given figure, O is the centre of the circle and OLM is perpendicular to AOB prove that (i) A, O, P and M are concyclic (i) ∠OAP=∠OMB (iii) P, L, O and B are concyclic
Step by step video & image solution for In the given figure, O is the centre of the circle and OLM is perpendicular to AOB prove that (i) A, O, P and M are concyclic (i) /_OAP =/_OMB (iii) P, L, O and B are concyclic by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
In the given figure, , O is the centre of a circle and ∠AOB=140∘. Then , ∠ACB=?
 A70∘B80∘C110∘D40∘
A70∘B80∘C110∘D40∘In the given figure, AC is the diameter of the circle with centre O. Chord BD is perpendicular to AC. Express p in terms of x.
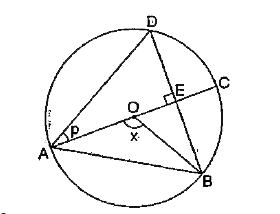 Ax/2B90∘+x/2C90∘−x/2D180∘−x
Ax/2B90∘+x/2C90∘−x/2D180∘−x
In Figure, O is the centre of a circle and PO BISECTS ∠APD. Prove that AB=CD
View SolutionIn Figure, find m ∠PQB where O is the centre of the circle
View SolutionIn the given figure, AOB is a diameter of a circle with centre O. Find tan A tan B.
View SolutionIn the given figure, O is the centre of a circle, ∠AOB=40∘ and ∠BDC=100∘, find ∠OBC.
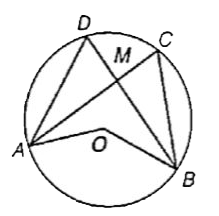
View SolutionIn the given figure of circle, ‘O’ is the centre of the circle ∠AOB=130∘. What is the value of ∠DMC?
View SolutionIn Figure, O is the centre of the circle. If ∠APB=500, find ∠AOB and ∠OAB
View Solution