In the given figure, O is the centre of the circle and OLM is perpendicular to AOB. Prove that (i) A, O, P and M are concyclic (ii) ∠OAP=∠OMB (iii) P, L, O and B are concyclic
To solve the given problem step by step, we will prove each part as required.
Given:
- O is the center of the circle.
- OLM is perpendicular to AOB.
To Prove:
1. A, O, P, and M are concyclic.
2. ∠OAP = ∠OMB.
3. P, L, O, and B are concyclic.
1. Identify Angles:
Since OLM is perpendicular to AOB, we have:
∠AOM=90∘
2. Use the Inscribed Angle Theorem:
Since A and P lie on the circle with diameter AM (because ∠APB = 90°), we have:
∠APM=90∘
3. Compare Angles:
Now, we have:
∠AOM=90∘and∠APM=90∘
Therefore, angles AOM and APM are equal.
4. Concyclic Points:
Since both angles are subtended by the same chord AM on the same side, it follows that points A, O, P, and M are concyclic.
Conclusion for Part (i):
- A, O, P, and M are concyclic.
---
Part (ii): Prove that ∠OAP = ∠OMB.
1. Use Inscribed Angles:
From part (i), we know that:
∠OAP and ∠OMB subtend the same arc OP.
2. Conclusion:
Therefore, we can conclude:
∠OAP=∠OMB
Conclusion for Part (ii):
- ∠OAP = ∠OMB.
---
Part (iii): Prove that P, L, O, and B are concyclic.
1. Sum of Opposite Angles:
In quadrilateral PLOB, we know:
∠P+∠O=90∘+90∘=180∘
2. Cyclic Quadrilateral Condition:
Since the sum of opposite angles in quadrilateral PLOB is 180°, it follows that P, L, O, and B are concyclic.
Conclusion for Part (iii):
- P, L, O, and B are concyclic.
---
Final Summary:
1. A, O, P, and M are concyclic.
2. ∠OAP = ∠OMB.
3. P, L, O, and B are concyclic.
---
- O is the center of the circle.
- OLM is perpendicular to AOB.
1. A, O, P, and M are concyclic.
2. ∠OAP = ∠OMB.
3. P, L, O, and B are concyclic.
Since OLM is perpendicular to AOB, we have:
∠AOM=90∘
Since A and P lie on the circle with diameter AM (because ∠APB = 90°), we have:
∠APM=90∘
Now, we have:
∠AOM=90∘and∠APM=90∘
Therefore, angles AOM and APM are equal.
Since both angles are subtended by the same chord AM on the same side, it follows that points A, O, P, and M are concyclic.
- A, O, P, and M are concyclic.
From part (i), we know that:
∠OAP and ∠OMB subtend the same arc OP.
Therefore, we can conclude:
∠OAP=∠OMB
- ∠OAP = ∠OMB.
In quadrilateral PLOB, we know:
∠P+∠O=90∘+90∘=180∘
Since the sum of opposite angles in quadrilateral PLOB is 180°, it follows that P, L, O, and B are concyclic.
- P, L, O, and B are concyclic.
1. A, O, P, and M are concyclic.
2. ∠OAP = ∠OMB.
3. P, L, O, and B are concyclic.
Topper's Solved these Questions
Similar Questions
In Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn Figure, O is the centre of a circle and PO BISECTS ∠APD. Prove that AB=CD
View SolutionIn Figure, O is the centre of the circle, prove that ∠x=∠y+∠z
View SolutionIn Figure, find m ∠PQB where O is the centre of the circle
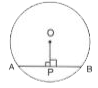
View SolutionThe following figure shows a circle with centre O.
If OP is perpendicular to AB, prove that AP = BP.
View SolutionIn figure O is the centre of the circle, prove that ∠z=∠x+∠y.

View SolutionIn the adjoining figure, O is the centre of the circle, Prove that ∠x=∠y+∠z.

View SolutionIn the given figure O is the centre of the circle. Tangents at A and B meet at C. If ∠ACO=30∘ find
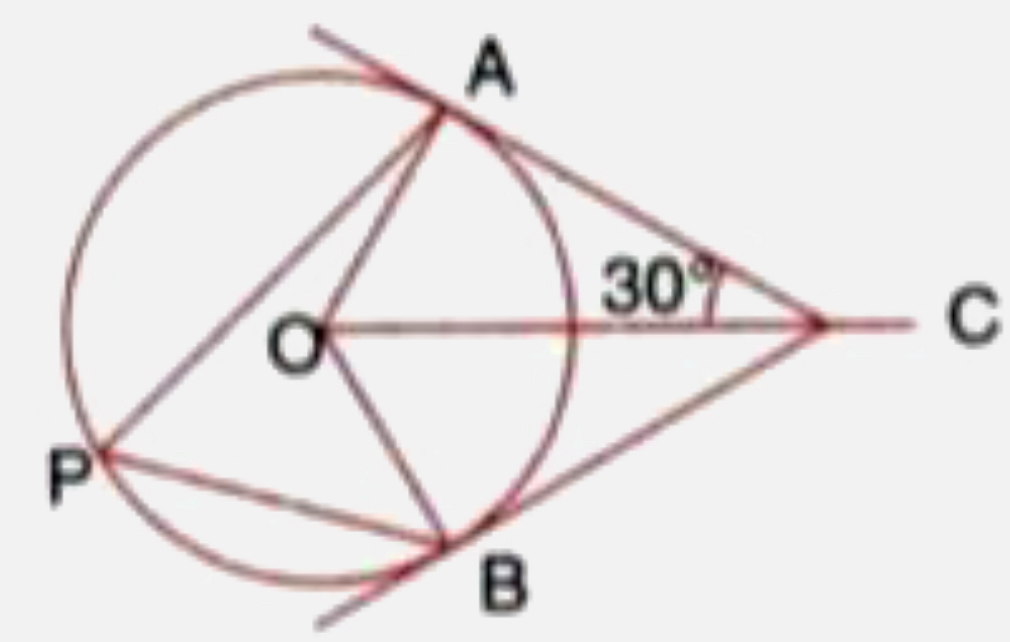
(i) ∠BCO
(ii) ∠AOB
(iii) ∠APB
View SolutionIn Figure, it is given that O is the centre of the circle and ∠AOC=150∘. Find ∠ABC
View SolutionIn Figure, O is the centre of the circle. If ∠APB=500, find ∠AOB and ∠OAB
View Solution