In a centre trap full wave rectifier, the load resistance RL=1kΩ. Each diode has a forward bias dynamic resistance 20Ω. The voltage across half the secondary winding is 110 sin 100 pit. Find (i) the peak value of current (ii) the dc value of current (iii) the rms value of current.
To solve the problem step by step, we will calculate the peak value of current, the DC value of current, and the RMS value of current for a center-tap full-wave rectifier.
Given Data:
- Load resistance, RL=1kΩ=1000Ω
- Forward bias dynamic resistance of each diode, Rd=20Ω
- Voltage across half the secondary winding, V(t)=110sin(100πt)
Step 1: Find the Peak Voltage
The peak voltage Vp is given directly from the voltage equation:
Vp=110V
Step 2: Calculate Total Resistance
The total resistance in the circuit is the sum of the load resistance and the dynamic resistance of the diode:
Rtotal=RL+Rd=1000Ω+20Ω=1020Ω
Step 3: Calculate the Peak Current
Using Ohm's Law, the peak current Ip can be calculated as:
Ip=VpRtotal=110V1020Ω≈0.1078A≈0.108A
Step 4: Calculate the DC Value of Current
The DC value of current IDC for a full-wave rectifier can be calculated using the formula:
IDC=2Ipπ=2×0.108Aπ≈0.0687A
Step 5: Calculate the RMS Value of Current
The RMS value of current IRMS can be calculated using the formula:
IRMS=Ip√2=0.108A√2≈0.0764A≈0.07638A
Summary of Results:
1. Peak Current, Ip≈0.108A
2. DC Current, IDC≈0.0687A
3. RMS Current, IRMS≈0.07638A
- Load resistance, RL=1kΩ=1000Ω
- Forward bias dynamic resistance of each diode, Rd=20Ω
- Voltage across half the secondary winding, V(t)=110sin(100πt)
The peak voltage Vp is given directly from the voltage equation:
Vp=110V
The total resistance in the circuit is the sum of the load resistance and the dynamic resistance of the diode:
Rtotal=RL+Rd=1000Ω+20Ω=1020Ω
Using Ohm's Law, the peak current Ip can be calculated as:
Ip=VpRtotal=110V1020Ω≈0.1078A≈0.108A
The DC value of current IDC for a full-wave rectifier can be calculated using the formula:
IDC=2Ipπ=2×0.108Aπ≈0.0687A
The RMS value of current IRMS can be calculated using the formula:
IRMS=Ip√2=0.108A√2≈0.0764A≈0.07638A
1. Peak Current, Ip≈0.108A
2. DC Current, IDC≈0.0687A
3. RMS Current, IRMS≈0.07638A
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - LONG QUESTION ANSWER2videos
ELECTRONIC DEVICES
- BOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - PROBLEMS FOR PRACTICE7videos
ELECTRONIC DEVICES
- BOOK - PRADEEPCHAPTER - ELECTRONIC DEVICESEXERCISE - HIGHER ORDER THINKING SKILLS1videos
ELECTRONIC DEVICES
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
- BOOK - PRADEEPCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION-REASON TYPE QUESTIONS2videos
ELECTROSTATICS
Similar Questions
In a centre trap full wave rectifier, the load resistance RL=1kΩ. Each diode has a forward bias dynamic resistance of 10Ω. The voltage across half the secondary winding is 220sin314t. Find (i) the peak value of current (ii) the dc value of current and (iii) the rms value of current.
View SolutionA full wave rectifier uses two diode, the internal resistance if each diode is 20Ω. The transformer rms seconary voltage from centre tap tp each end of secondary is 50 V and load resistance is 980Ω. Find (i) the mean load current (ii) the rms value of load current.
View Solution
Knowledge Check
- Question 1 - Select One
The instantaneous voltage through a device of impendance 20 Ω is V=80sin100πt. The effective value of the current is
A0.125B2.828 AC1.732 AD0.16666666666667 - Question 2 - Select One
In input in a full - wave rectifier is e=50sin(314t) volt, diode resistance is 100Ω and load resistance is 1kΩ then, pulse frequency of output voltage is
A50 HzB100 HzC150 HzD200 Hz
A full wave rectifier uses two diodes with a load resistance of 100Ω. Each diode is having negligible forward resistance. Find the efficiency of this wave rectifier.
View SolutionA full wave rectifier uses two diodes, the internal resistance of each diode may be assumed constant at 25Ω. The transformer r.m.s. secondary voltage from centre tap to each end of the secondary is 50V and load current (ii) the rms value of load current.
View SolutionAn laternativing voltage of 350 V, 60 Hz is applied on a full wave rectifier. The internal resistance of each diode is 200Ω. If RL=5kΩ, then find
(i) the peak value of output current.
(ii) the value of output direct current.
(iii) the output dc power.
(iv) the rms value of output current.
(v) the efficiency of rectifier.
(vi) the value of peak inverse voltage (P.I.V.).View SolutionA full wave rectifier uses two diodes, the internal resistance of each diode may be assumed constant at 30Ω. The transformer r.m.s. secondary voltage from centre tap to each end of the secondary is 50 V and load resistance is 970Ω. Find (i) the mean load current (ii) the rms value of load current.
View SolutionIn the given figure, each diode has a forward bias resistance of 30Ω and infinite resistance in reverse bias. The current I1 will be :
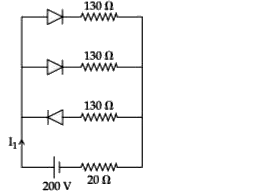 View Solution
View SolutionIn the given figure, each diode has a forward bias resistance of 30Ω and infinite resistance in reverse bias. The current I1 will be :
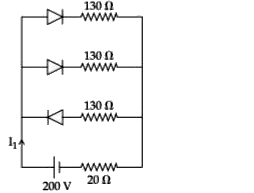 View Solution
View Solution

