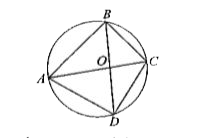
O is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P. If ∠AOB=15∘ and ∠APB=30∘, then 3(tan2∠APB+cot2∠COD) is equal to
Step by step video & image solution for O is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P. If angleAOB =15^@ and angleAPB =30^@, then 3(tan^2angleAPB+ cot^2angleCOD) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
O is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P, If ∠AOB=15∘and∠APB=30∘, then ∠COD is equal to
View SolutionO is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P. If ∠AOB=15∘ and ∠APB=30∘, then 3(tan2∠APB+cot2∠COD) is equal to
View Solution
Knowledge Check
O is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P. If ∠AOB=15∘and∠APB=30∘, then tan2∠APB+cot2∠COD is equal to :
A43B103C13D23If AC and BD are two chords of a circle that bisect each other then quadrilateral ABCD is a
 ArectangleBsquareCtrapeziumDparallelogram
ArectangleBsquareCtrapeziumDparallelogramTwo chords AB, CD of a circle with centre O intersect each other at P. ∠ADP=23∘ and ∠APC=70∘, then the ∠BCDis
A45∘B47∘C57∘D67∘
The centre of circle is O. AC and BD are chords of circle which intersect at P. If ∠AOB=15∘ and ∠APB=30∘ thentan2∠APB+cot2∠COD is-
View SolutionIn the given figure O is the centre of the circle AC and BD intersects at P. If ∠AOB=100∘ and ∠DAP=30∘ then what is the value of ∠APB?
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
View SolutionThe diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC=32∘and∠AOB=70∘, then ∠DBC is equal to
View SolutionTwo chords AB and CD of a circle with centre o intersect each other at the point P. If ∠AOD=20∘ and ∠BOC=30∘, then ∠BPCis equal to:
View Solution
