The centre of circle is O. AC and BD are chords of circle which intersect at P. If ∠AOB=15∘ and ∠APB=30∘ thentan2∠APB+cot2∠COD is-
13
23
43
103
To solve the problem, we need to find the value of tan2∠APB+cot2∠COD given that ∠AOB=15∘ and ∠APB=30∘.
1. Identify Given Angles:
- We have ∠AOB=15∘.
- We have ∠APB=30∘.
2. Find ∠COD:
- Since AC and BD are chords intersecting at point P, we can use the property of angles formed by intersecting chords.
- The angle at the center O is twice the angle at the circumference that subtends the same arc. Therefore, we can express ∠COD in terms of ∠AOB and ∠APB.
- Let α=∠APB and β=∠AOB.
- We know that ∠COD=2×∠APB (since ∠COD subtends the same arc as ∠APB).
- Thus, ∠COD=2×∠APB=2×30∘=60∘.
3. Calculate tan2∠APB:
- We know ∠APB=30∘.
- Therefore, tan∠APB=tan30∘=1√3.
- Now, calculate tan2∠APB:
tan2∠APB=(1√3)2=13.
4. Calculate cot2∠COD:
- We know ∠COD=60∘.
- Therefore, cot∠COD=cot60∘=1tan60∘=1√3.
- Now, calculate cot2∠COD:
cot2∠COD=(1√3)2=13.
5. Combine the Results:
- Now, we can find tan2∠APB+cot2∠COD:
tan2∠APB+cot2∠COD=13+13=23.
Final Result:
Thus, the final answer is:
tan2∠APB+cot2∠COD=23.
- We have ∠AOB=15∘.
- We have ∠APB=30∘.
- Since AC and BD are chords intersecting at point P, we can use the property of angles formed by intersecting chords.
- The angle at the center O is twice the angle at the circumference that subtends the same arc. Therefore, we can express ∠COD in terms of ∠AOB and ∠APB.
- Let α=∠APB and β=∠AOB.
- We know that ∠COD=2×∠APB (since ∠COD subtends the same arc as ∠APB).
- Thus, ∠COD=2×∠APB=2×30∘=60∘.
- We know ∠APB=30∘.
- Therefore, tan∠APB=tan30∘=1√3.
- Now, calculate tan2∠APB:
tan2∠APB=(1√3)2=13.
- We know ∠COD=60∘.
- Therefore, cot∠COD=cot60∘=1tan60∘=1√3.
- Now, calculate cot2∠COD:
cot2∠COD=(1√3)2=13.
- Now, we can find tan2∠APB+cot2∠COD:
tan2∠APB+cot2∠COD=13+13=23.
Thus, the final answer is:
tan2∠APB+cot2∠COD=23.
Topper's Solved these Questions
Similar Questions
O is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P. If ∠AOB=15∘ and ∠APB=30∘, then 3(tan2∠APB+cot2∠COD) is equal to
View SolutionO is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P, If ∠AOB=15∘and∠APB=30∘, then ∠COD is equal to
View Solution
Knowledge Check
O is the centre of a circle. AC and BD are two chords of the circle intersecting each other at P. If ∠AOB=15∘and∠APB=30∘, then tan2∠APB+cot2∠COD is equal to :
A43B103C13D23Two tangents drawn at the points A and B of a circle centred at O meet at P. If ∠AOB=120∘ then ∠APB:∠APO is
A2:5B3:2C4:1D2:1ABCD is a cyclic quadrilateral. Diagonals AC and BD meets at P. If ∠APB=110∘ and ∠CBD=30∘, then ∠ADB measures
A55∘B30∘C70∘D80∘
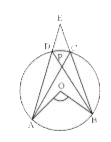
In the given figure O is the centre of the circle AC and BD intersects at P. If ∠AOB=100∘ and ∠DAP=30∘ then what is the value of ∠APB?
View SolutionTwo chords AB and CD of a circle with centre O intersect at P. If ∠APC=40∘. Then the value of ∠AOC+∠BOD is
View SolutionThe point of intersection for the diagonals AC and BD of the cyclic quadrilateral ABC is P. If ∠APB=64∘ and ∠CBD=28∘, the measure of ∠ADB is
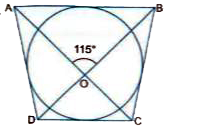
View SolutionIn Fig the quadrilateral ABCD circumscribes a circle with centre O. If ∠AOB=115∘, then find ∠AOB=115∘ then find ∠COD.
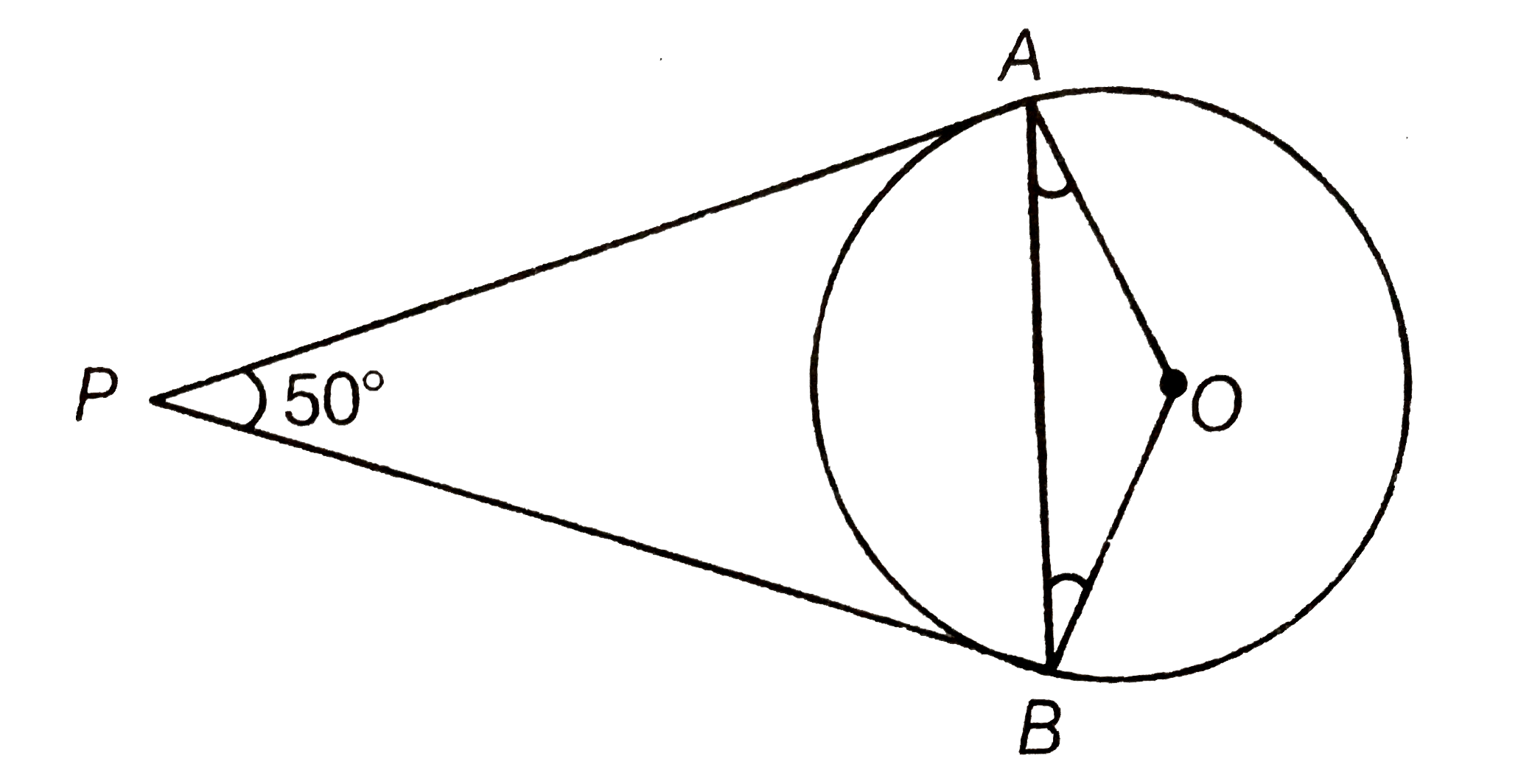
View SolutionIn figure, if PA and PB are tangents to the circle with centre O such that ∠APB=50∘, then ∠OAB is equal to
View Solution
