The acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
g'∝1r2
g'∝r
g'∝1r
g'∝r2
The correct Answer is:B
The distance r is measured from the centre of the earth.
∴ It is at a depth d = R - r from the surface of the earth.
∵g'=g[1−dR]
∴g'=g[1−R−rR]=g[R−R+rR]=grR
∴g'∝r
Topper's Solved these Questions
- GRAVITATION BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -2
20 Videos
- ELECTROSTATICSBOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP
20 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - MARVEL PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - TEST YOUR GRASP
20 Videos
Similar Questions
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be sphere of radius R of uniform density is a shown in figures along side.
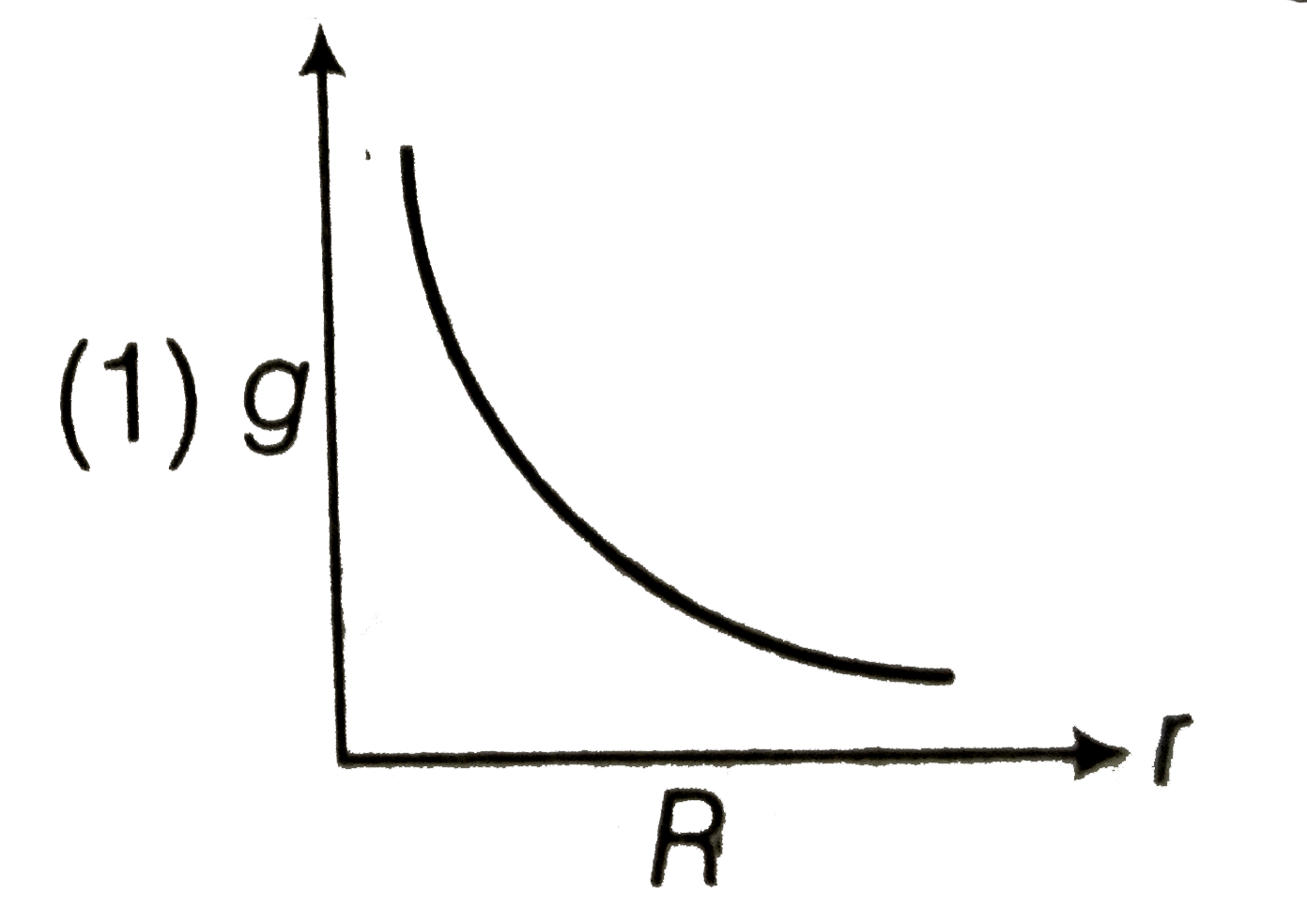
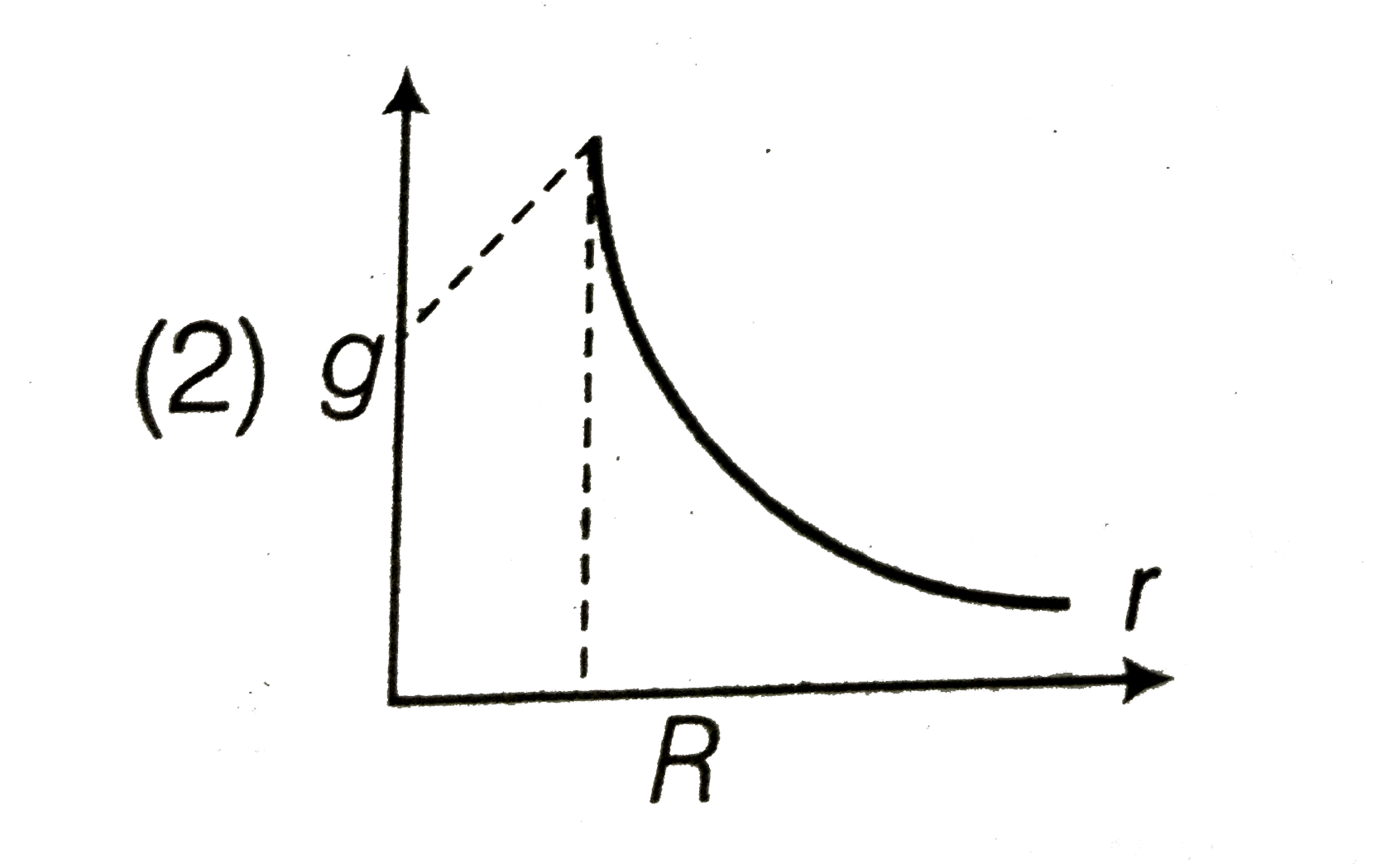
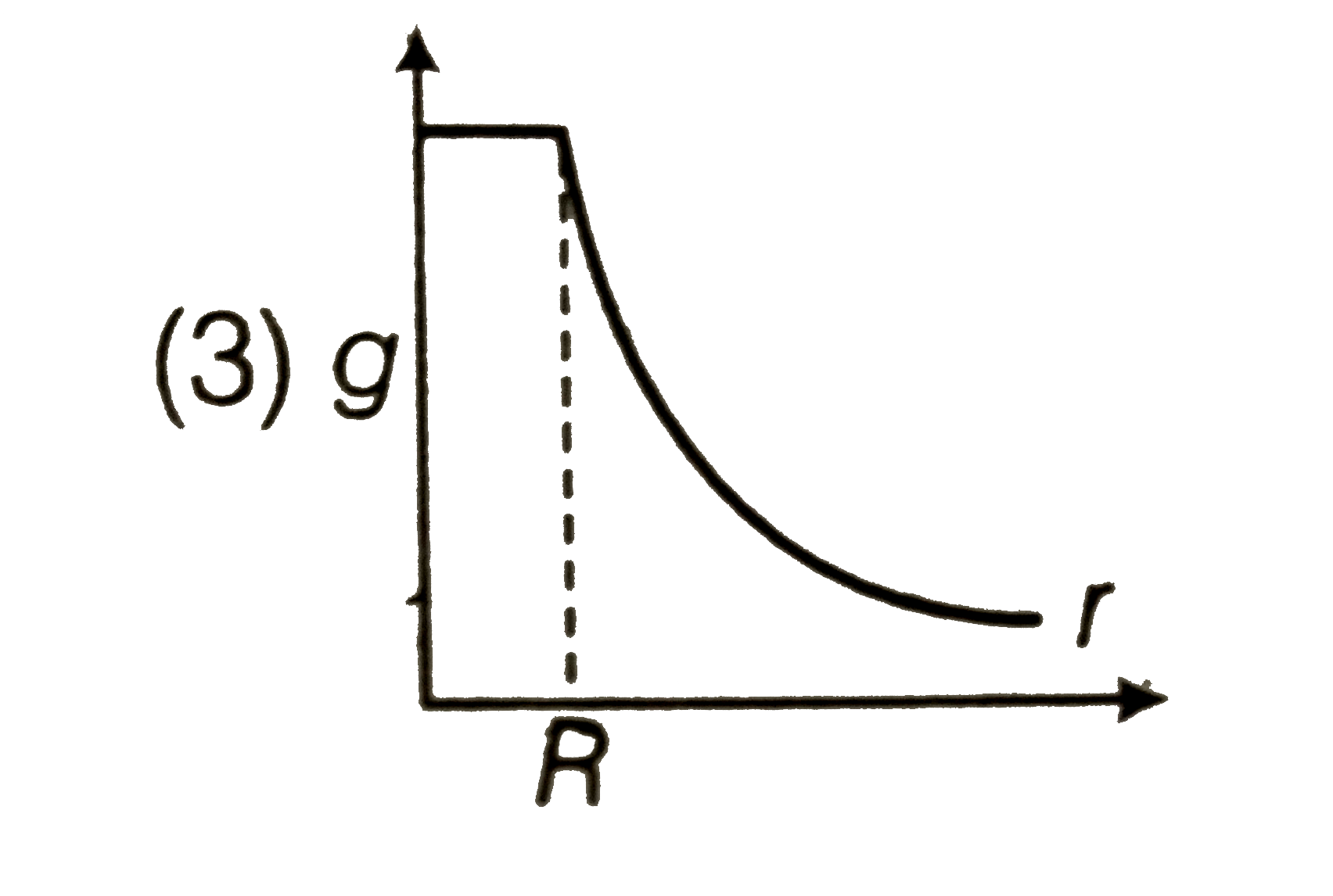
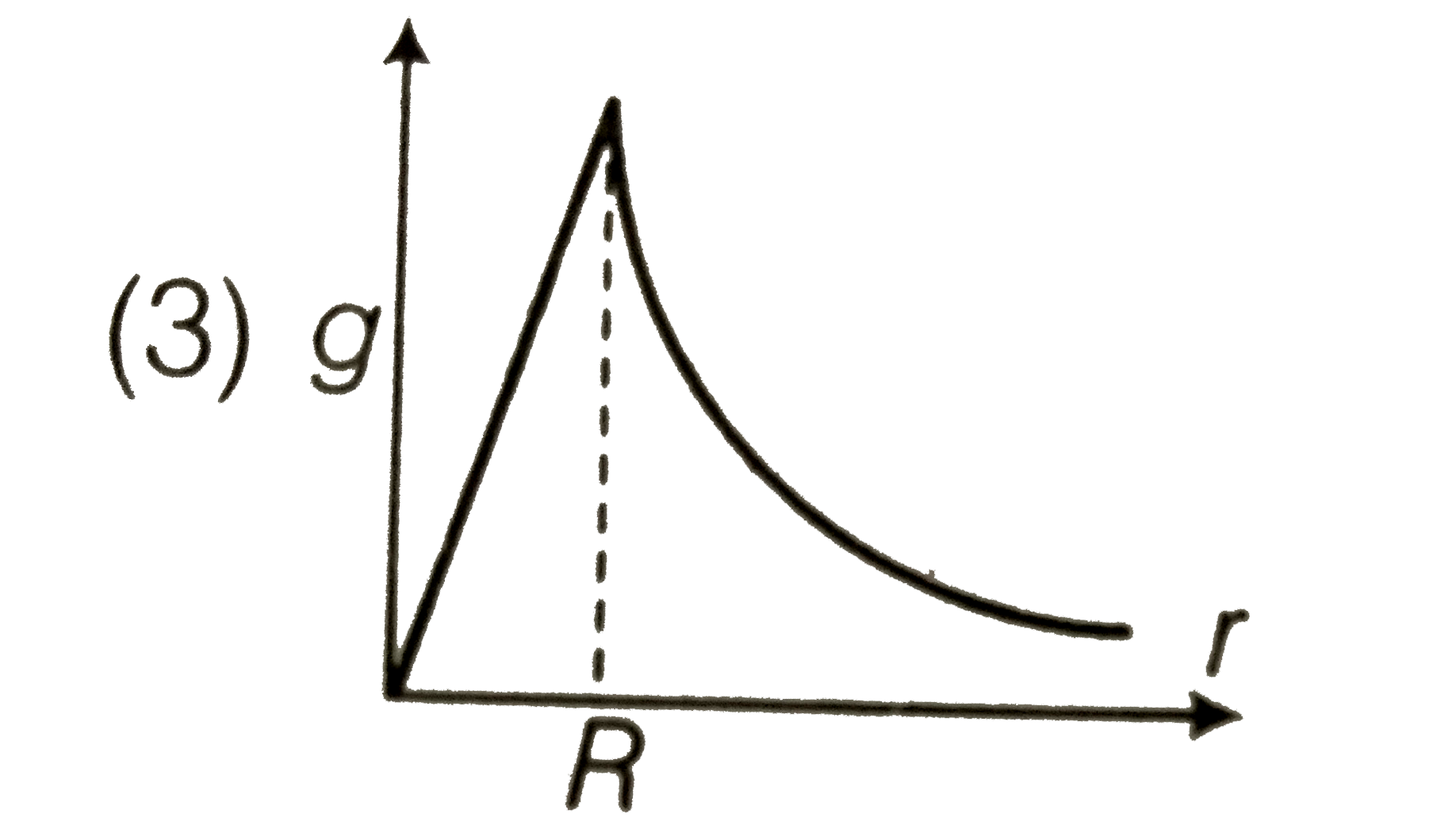
The correct figure is
View SolutionThe acceleration due to gravity at a depth R/2 below the surface of the earth is
View Solution
Knowledge Check
If g denotes the value of acceleration due to gravity at a point distance r from the centre of earth of radius R. If r<R, then
Ag∝r2Bg∝rCg∝1/r2Dg∝1/rThe dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to br a sphere of radius R of uniform density is as shoen in Fig. below:

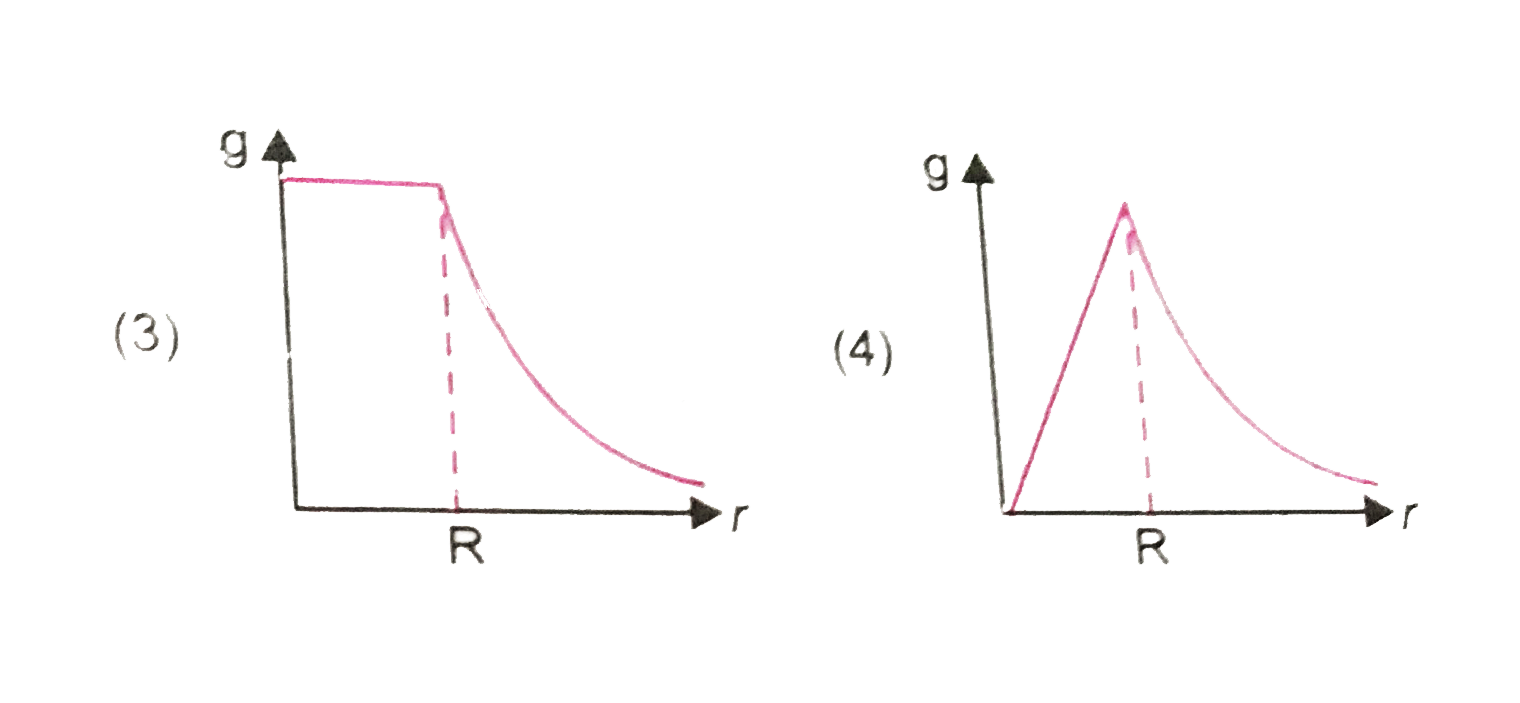
The correct figure isA(4)B(1)C(2)D(3)If R= radius of the earth and g= acceleration due to gravity on the surface of the earth, the acceleration due to gravity at a distance (r<R) from the centre of the earth is proportional to
ArBr2Cr−2Dr−1
The value of the acceleration due to gravity is g1 at a height h=(R)/(2)(R= radius of the earth) from the surface of the earth.It is again equal to (g1/2) at a depth d below the surface of the earth.The ratio d/R equals:
View SolutionIf R= radius of the earth and g= acceleration due to gravity on the surface of the earth, the acceleration due to gravity at a distance (r>R) from the centre of the earth is proportional to
View SolutionThe acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
View SolutionVariation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by (R→ Radius of the Earth)
View SolutionIf acceleration due to gravity at distance d [<R] from the centre of earth is β , then its value at distance d above the surface of earth will be [ where R is radius of earth ]
View Solution
