The charge and energy stored in the capacitor of capacity 32μF, when it is charged to a potential difference of 0.6 kV are respectively
1.92×10−2C,5.76J
2.92×10−2C,5.76J
1.92×102C,5.76J
1.92×10−2C,4.76J
The correct Answer is:A
Q = CV
=32×10−6×0.6×103=1.92×10−2C
E=12CV2=32×10−6×(0.6×103)22=5.76J.
Topper's Solved these Questions
Similar Questions
Calculate energy stored in a capacitor stored in a capacitor of 5μF when it is charged to a potential of 250 volt.
View SolutionA capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the parallel combination of two capacitors.
View Solution
Knowledge Check
Find the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
A0.02JB0.04JC0.01JD0.05JIn the circuit shown in figure charge stored in the capacitor of capacity 5μF is
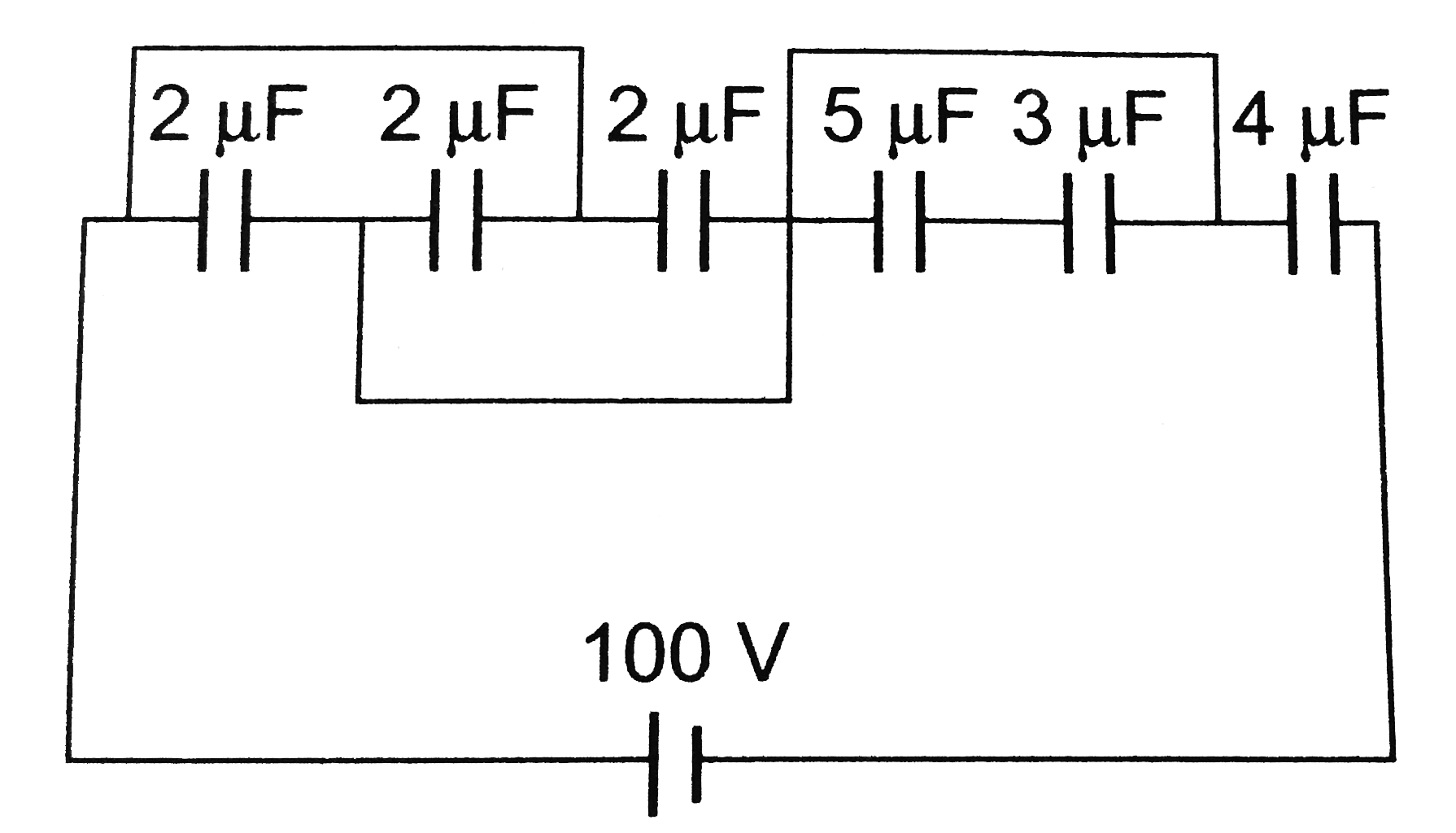 A60μCB20μCC30μCDzero
A60μCB20μCC30μCDzeroA and B are two condensers of capacities 2μF and 4μF. They are charged to potential differences of 12V and 6V respectively. If they are now connected (+ve to +ve), the charge that flows through the connecting wire is
A24μC from A to BB8μC from A to BC8μC from B to AD24μC from B to A
A capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the two capacitors before they are connected .
View SolutionA capacitor of capacitance 5 μF is charged to a potential difference of 10 volts and another capacitor of capacitance 9 μF is charged to a potential difference of 8 volts. Now these two capacitors are connected in such a manner that the positive plate of one is connected to the positive plate of other. Calculate the common potential difference across the two capacitors.
View SolutionTwo capacitors A and B with capacities 3μF and 2μF are charged to a potential difference of 100V and 180V, respectively. The plates of the capacitors are connected as show in figure with one wire of each capacitor free. The upper plate of A is positive and that of B is negastive. An uncharged 2μF capcitor C with lead wires falls on the free ends to complete the circuit. Calculate
a. the final charge on the three capacitors.
b. the amount of electrostatic energy stored in the system before and after completion of the circuit.
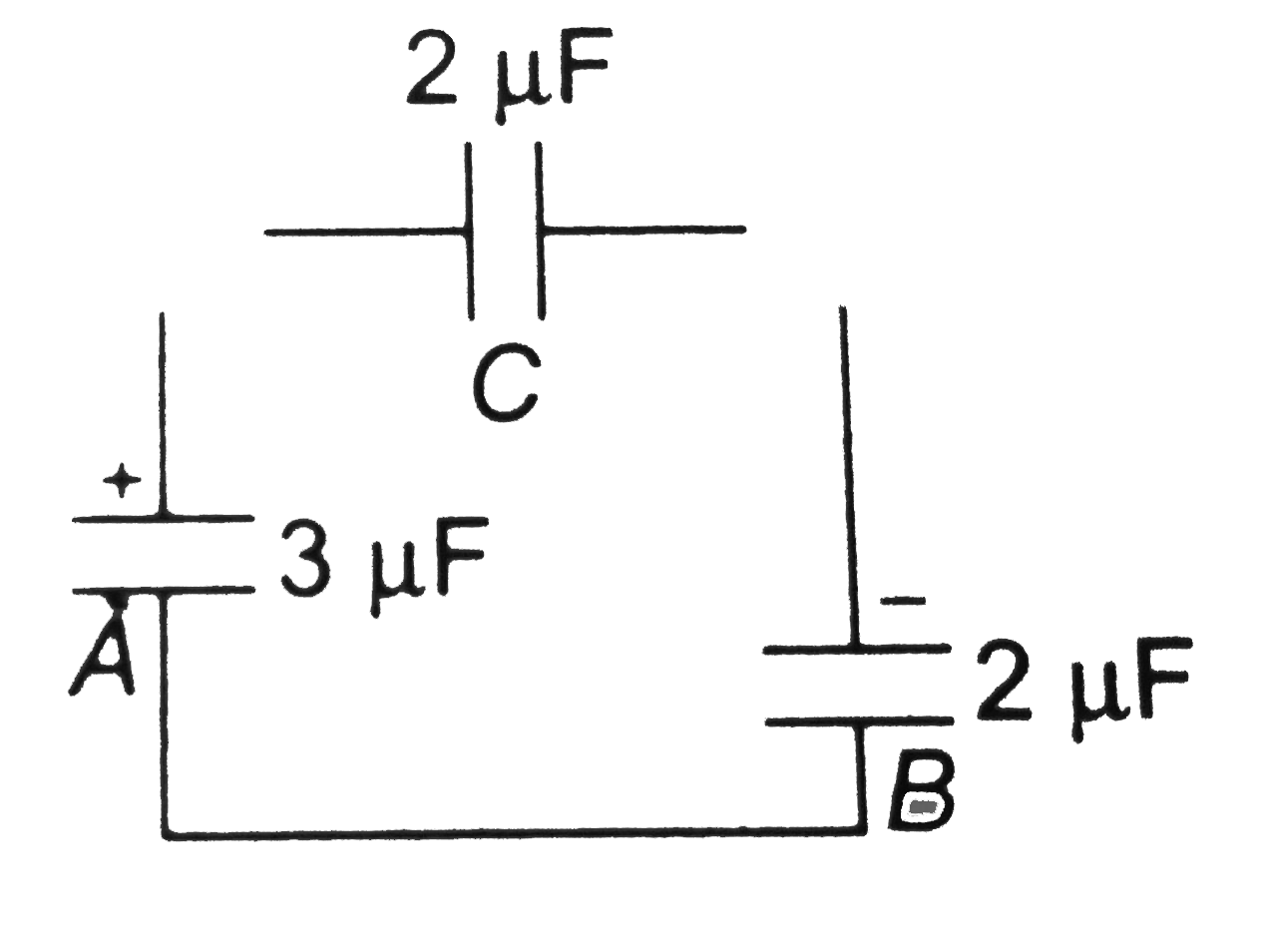
View SolutionA capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionTwo capacitors A and B with capacities 3μF and 2μF are charged to a potential differece of 100V and 180V, respectively. The plates ot the capacitors are connected as shown in, with one wire free from each capacitor. The upper plate of A is positive and that of B is negative An uncharged 2μF capacitor C with lead wires falls on the free ends to complete the circuit.
i. Calculate the final charge on the three capacitors,
ii. Find the amount of electrostatic energy stored in the system before and after the completion of the circuit.
 .
.
View Solution
