The distance of the point $(3, 8, 2)$ from the line $\frac{x - 1}{4} = \frac{y - 3}{4} = \frac{z - 2}{3}$ measured parallel to the plane $\to r . (3 ˆ i + 2 ˆ j - 2 ˆ k) = 15$ is __Solution in Bengali

Video Solution

Text Solution

Verified by Experts

The correct Answer is:7

Updated on:21/07/2023

Answer

Step by step video, text & image solution for The distance of the point (3,8,2) from the line (x-1)/(4) =(y-3)/(4)=(z-2)/(3) measured parallel to the plane vec r .( 3 hati +2 hatj-2 hatk)=15 is __ by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

PLANE BOOK - CHHAYA PUBLICATIONCHAPTER - PLANE EXERCISE - Sample Question for Competitive Examination( C Matrix Match Type )
1 Videos
PLANE BOOK - CHHAYA PUBLICATIONCHAPTER - PLANE EXERCISE - Sample Question for Competitive Examination( D Comprehension Type )
7 Videos
PLANE BOOK - CHHAYA PUBLICATIONCHAPTER - PLANE EXERCISE - Sample Question for Competitive Examination
5 Videos
PERMUTATION AND COMBINATION BOOK - CHHAYA PUBLICATIONCHAPTER - PERMUTATION AND COMBINATION EXERCISE - Sample Questions for Competitive Exams E Assertion -Reason Type
2 Videos
PROBABILITYBOOK - CHHAYA PUBLICATIONCHAPTER - PROBABILITYEXERCISE - SAMPLE QUESTIONS FOR COMPETITIVE EXAMS
18 Videos

Similar Questions

Match the following Column I and Column II
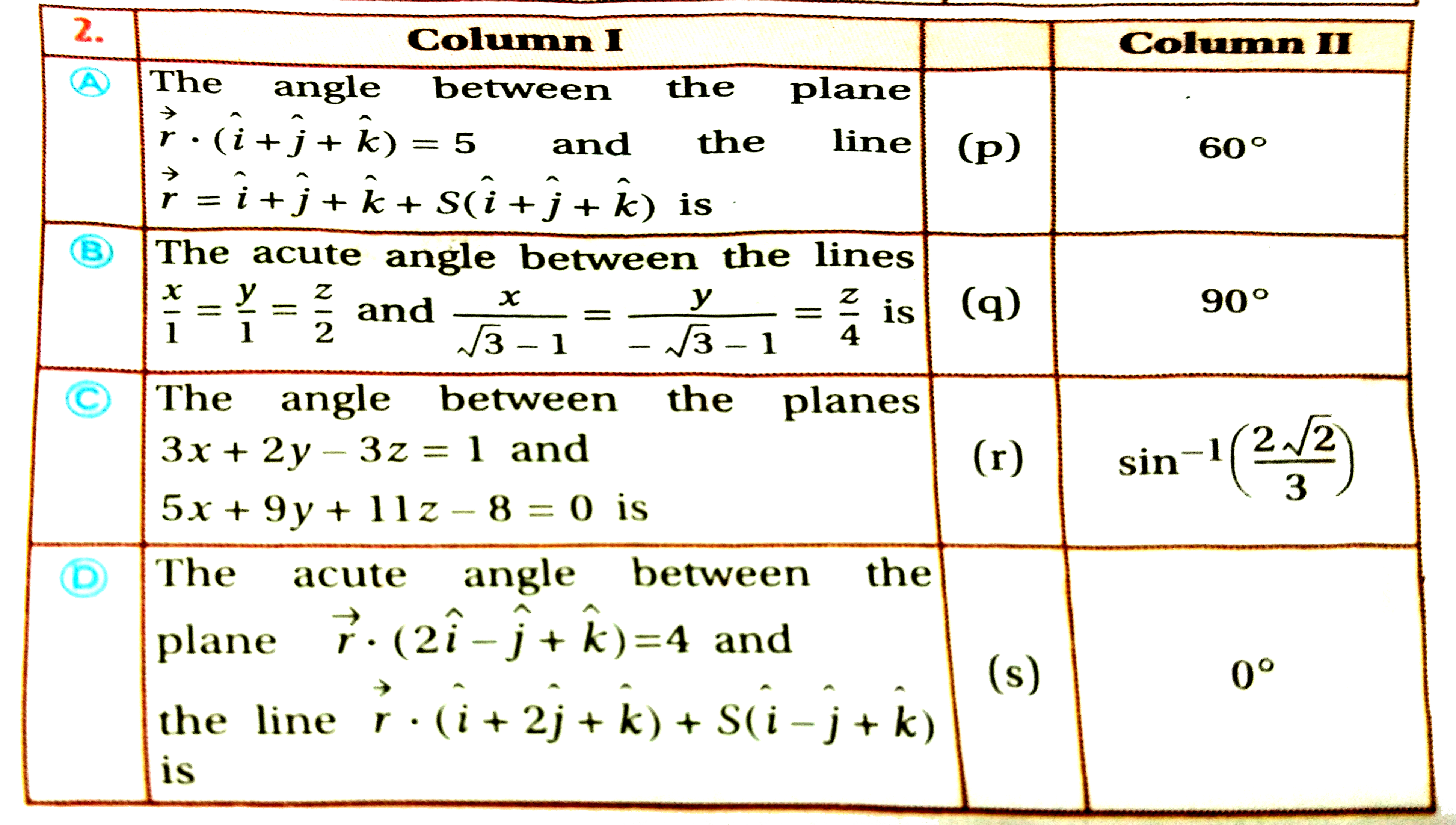
View Solution
The distance of the point P from the plane p from the plane p is __
View Solution
Consider the plane $3 x - 6 y + 2 z + 5 = 0$ and $4 x - 12 y + 3 z = 3$ . The plane $67 x - 162 y + 47 z + 44 = 0$ bisects the angle between the given planes which__
View Solution
Statement -I : Number of terms in the expansion of ${(x + y + z + w)}^{50}$ is $.^{53} C_{3}$ .
Statement -II : Number of non- negative solution of the equation $p + q + r + s = 50$ is $.^{53} C_{3}$ .
View Solution
If A and B are two independent events of a random experiment and $P (A) = \frac{1}{2} /, P (B) = \frac{1}{5},$ then -
View Solution
Find the equation of the straight line passing (a) (i) through the point (1,-3, 2) and is perpendicular to the lines: (x-1)/1=(y-2)/2=(z-3)/3 and (x-3)/-3=(y-2)/2=(z-1)/5 (ii) through the point (2, 3,-1) and is perpendicular to the lines: (x-2)/2=(y+1)/1=(z-3)/-3 and (x-3)/1=(y+2)/1=(z-1)/1 (b) through the point (2,-1, 3) and perpendicular to the lines: vec r=(hati-hatj+hatk)+lambda(2hati+hatj-3hatk) and vec r=(hati+hatj-hatk)+mu(hati+hatj+hatk).
View Solution
Find the distance of the point $P (3, 8, 2)$ from the line $\frac{1}{2} (x - 1) = \frac{1}{4} (y - 3) = \frac{1}{3} (z - 2)$ measured parallel to the plane $3 x + 2 y - 2 z + 15 = 0 .$
View Solution
Find the distance of the point $(3, 8, 2)$ from the line $\to r = ˆ i + 3 ˆ j + 2 ˆ k + λ (2 ˆ i + 4 ˆ j + 3 ˆ k)$ measured parallel to the plane $\to r . (3 ˆ i + 2 ˆ j - 2 ˆ k) + 15 = 0 .$
View Solution
Find the shortest distance and the vector equation of the line of shortest distance between the lines given by :
$(i) \to r = (- 4 ˆ i + 4 ˆ j + ˆ k) + λ (ˆ i + ˆ j - ˆ k)$
and $\to r = (- 3 ˆ i - 8 ˆ j - 3 ˆ k) + μ (2 ˆ i + 3 ˆ j + 3 ˆ k)$
$(i i) \to r = (- ˆ i + 5 ˆ j) + λ (- ˆ i + ˆ j + ˆ k)$
and $\to r = (- ˆ i - 3 ˆ j + 2 ˆ k) + μ (3 ˆ i + 2 ˆ j + ˆ k) .$
View Solution
Show that the lines :
$\to r = 3 ˆ i + 2 ˆ j - 4 ˆ k + λ (ˆ i + 2 ˆ j + 2 ˆ k)$
and $\to r = 5 ˆ i - 2 ˆ j + μ (3 ˆ i + 2 ˆ j + 6 ˆ k)$
(ii) $\to r = (ˆ i + ˆ j - ˆ k) + λ (3 ˆ i - ˆ j)$ .
and $\to r = (4 ˆ i - ˆ k) + μ (2 ˆ i + 3 ˆ k)$
are intersecting. Hence, find their point of intersection.
View Solution
Show that the lines :
(a) $\frac{x - 1}{3} = \frac{y + 1}{5} and \frac{x - 2}{4} = \frac{y - 1}{3} = \frac{z + 1}{- 2}$
(b) $\to r = (ˆ i + ˆ j) + λ (2 ˆ i - ˆ k)$
and $\to r = (2 ˆ i - ˆ j) + μ (ˆ i + ˆ k - ˆ k)$ do not intersect.
View Solution
Angle between the planes:
(i) $\to r . (ˆ i - 2 ˆ j - ˆ k) = 1 and \to r . (3 ˆ i - 6 ˆ j + 2 ˆ k)$ = 0
(ii) $\to r . (2 ˆ i + 2 ˆ j - 3 ˆ k) = 5 and \to r . (3 ˆ i - 3 ˆ j + 5 ˆ k) = 3$
View Solution
Find the value of 'm' for which the line $\to r = (ˆ i + 2 ˆ k) + λ (2 ˆ i - m ˆ j - 3 ˆ k)$ is parallel to the plane
$\to r . (m ˆ i + 3 ˆ j + ˆ k)$ = 4.
View Solution
(i) Find the distance of the point (-1,-5,-10) from the point of intersection of the line $\to r = (2 ˆ i - ˆ j + 2 ˆ k) + λ (3 ˆ i + 4 ˆ j + 12 ˆ k)$ and the plane $\to r . (ˆ i - ˆ j + ˆ k) = 5 .$
(ii) Find the distance of the point with position vector
$- ˆ i - 5 ˆ j - 10 ˆ k$ from the point of intersection of the line $\to r = (2 ˆ i - ˆ j + 2 ˆ k) + λ (3 ˆ i + 4 ˆ j + 12 ˆ k)$ and the plane $\to r . (ˆ i - ˆ j + ˆ k) = 5 .$
(iii) Find the distance of the point (2,12, 5) from the point of intersection of the line .
$\to r = 2 ˆ i - 4 ˆ j + 2 ˆ k + λ (3 ˆ i + 4 ˆ j + 12 ˆ k)$
and the plane $\to r . (ˆ i - 2 ˆ j + ˆ k) = 0 .$
View Solution
Find the vector and cartesian equations of the plane containing the lines :
$\to r = ˆ i + 2 ˆ j - 4 ˆ k + λ (2 ˆ i + 3 ˆ j + 6 ˆ k)$ and
$\to r = 3 ˆ i + 3 ˆ j - 5 ˆ k + μ (- 2 ˆ j + 3 ˆ j + 8 ˆ k)$ .
View Solution

CHHAYA PUBLICATION-PLANE -Sample Question for Competitive Examination( B Integer Answer Type )

If the distance between the plane x-2y+z=d and the plane containing t...
06:50
A plane meets the coordinates axes respectively at A, B and C such th...
05:39
If the angle between the plane vecr .( hati-3 hatj+ 2 hatk)=15 and the...
03:13
The distance of the point (3,8,2) from the line (x-1)/(4) =(y-3)/(4)=(...
09:46
If the prependicular distance of a plane from the origin is 1 and dire...
05:05

Home
Ask Doubt
Profile

The distance of the point (3,8,2) from the line x−14=y−34=z−23 measured parallel to the plane →r.(3ˆi+2ˆj−2ˆk)=15 is __Solution in Bengali

The correct Answer is:7

Topper's Solved these Questions

Similar Questions

CHHAYA PUBLICATION-PLANE -Sample Question for Competitive Examination( B Integer Answer Type )

The distance of the point $(3, 8, 2)$ from the line $\frac{x - 1}{4} = \frac{y - 3}{4} = \frac{z - 2}{3}$ measured parallel to the plane $\to r . (3 ˆ i + 2 ˆ j - 2 ˆ k) = 15$ is __Solution in Bengali