ΔABC and ΔBDE are two equilateral triangles. If D is the mid-point of BC, then the ratio of the areas of ΔABC and ΔBDE isSolution in Bengali
2:1
1:2
1:4
4:1
Step by step video & image solution for DeltaABC and DeltaBDE are two equilateral triangles. If D is the mid-point of BC, then the ratio of the areas of DeltaABC and DeltaBDE is by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITYBOOK - CALCUTTA BOOK HOUSECHAPTER - SIMILARITYEXERCISE - Exercise 5.1
32 Videos
- SAMPLE QUESTIONS PAPERSBOOK - CALCUTTA BOOK HOUSECHAPTER - SAMPLE QUESTIONS PAPERSEXERCISE - QUESTION
157 Videos
- SIMPLE INTERESTBOOK - CALCUTTA BOOK HOUSECHAPTER - SIMPLE INTERESTEXERCISE - Long-answer type questions
37 Videos
Similar Questions
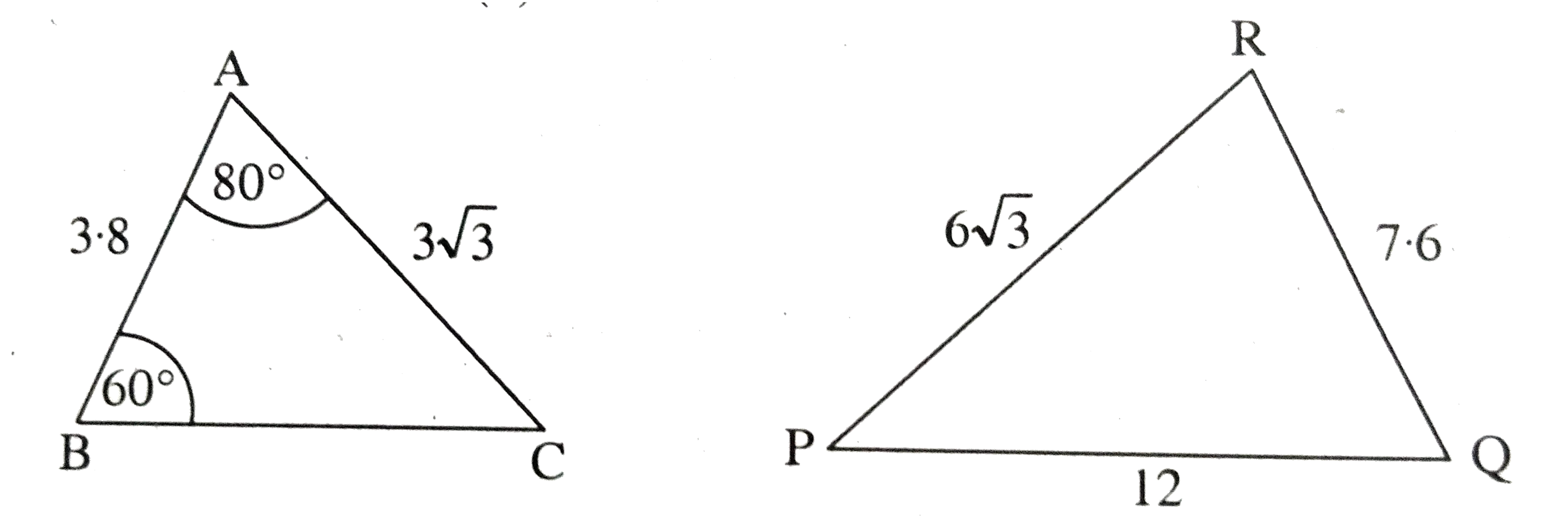
In the following figure , ∠P=
View SolutionA person deposite ₹ 100 in a bank and after 2 yars he got a total ₹121 as a return. Then the componund interest of the bank per annum is
View SolutionGoutam took a loan of some money from a cooperative bank for opening a poultry farm at the rate of simple interest of 12% per annum. Every month he has to repay 378Rs as interest. Determine the loan amount taken by him.
View SolutionABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)

View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC

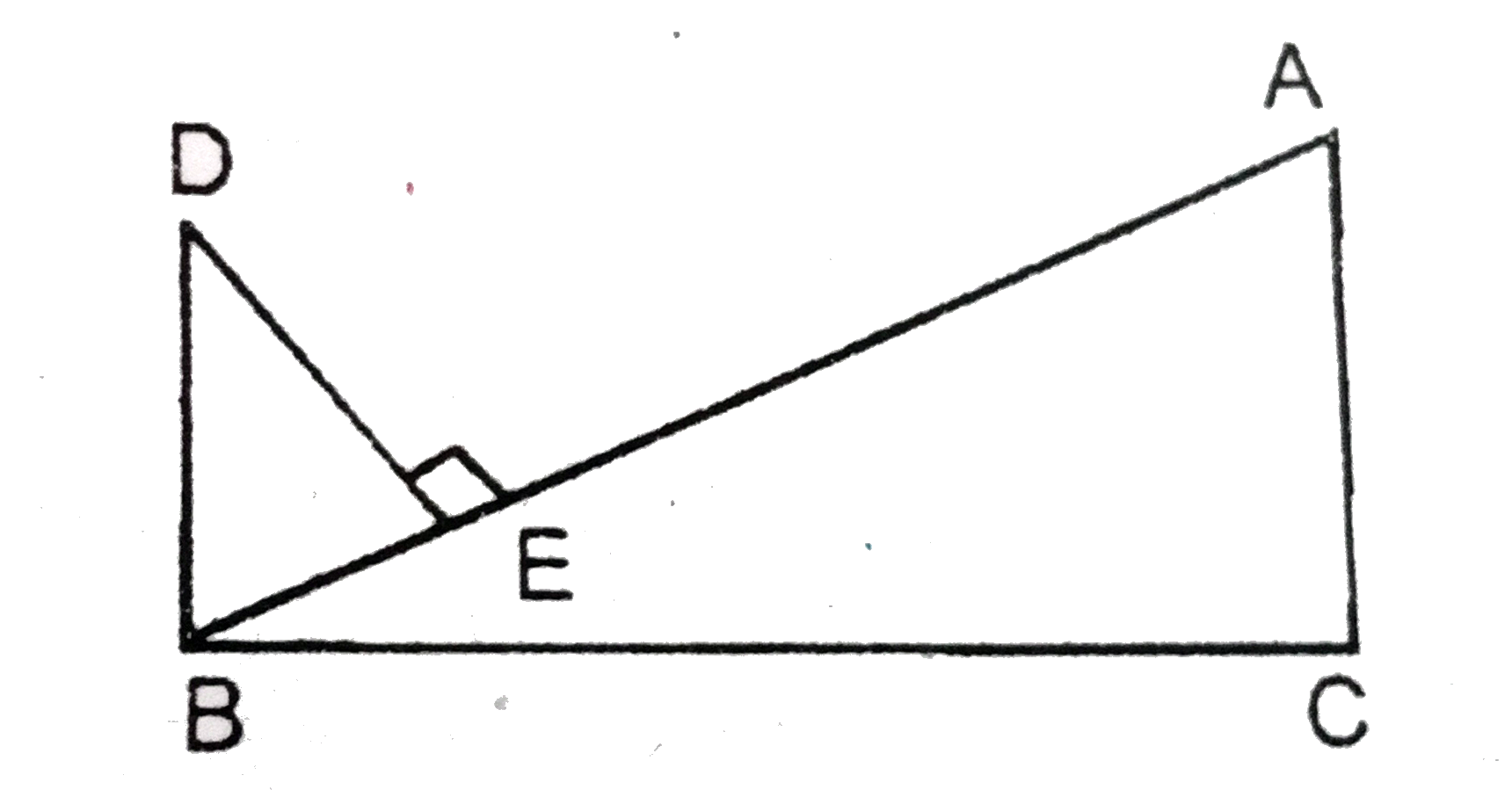
View Solutionदिए गये चित्र में DB⊥BC,DE⊥AB और AC⊥BC, तो सिद्ध करें कि ΔBDE~ΔABC.
View SolutionΔABC and ΔBDE are two equilateral triangles such that D is the midpoint of BC. Ratio of the areas of triangles ΔABC and ΔBDE is
View SolutionD,Eand F are respectively the mid - points of sides AB, BC and CA of ΔABC . Find the ratio of the areas of ΔDEFandΔABC.
View SolutionD, E and F are the mid-points of AB, BC and CA of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.
View SolutionD is the mid-point of BC of ΔABC. E and O are the mid-points of BD and AE respectively. Then the area of the triangle BOE is-
View SolutionABC is a triangle and D,E,F are the mid-points of the sides BC,CA, AB respectively . The ratio of the areas of ΔABCandΔDEF is :
View SolutionThe triangle is formed by joining the mid point of the sides AB, BC and CA of ΔABC and the area of ΔPQR is 6cm2, then the area of ΔABC is :
View SolutionIf D is the mid-point of the side BC of ΔABCand the area of ΔABD and the area of ΔACD is 16cm2, then the area of ΔABC is
View SolutionThe area of ΔABC is 44 cm2 . If D is the midpoint of BC and E is the midpoint of AB, then the area ( in cm2) of ΔBDE is :
View Solution
