If the ratio of the sides of two similar triangles be 4:9, then ratio of areas will beSolution in Bengali
16:81
2:3
4:9
81:16
Step by step video & image solution for If the ratio of the sides of two similar triangles be 4:9, then ratio of areas will be by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITYBOOK - CALCUTTA BOOK HOUSECHAPTER - SIMILARITYEXERCISE - Exercise 5.1
32 Videos
- SAMPLE QUESTIONS PAPERSBOOK - CALCUTTA BOOK HOUSECHAPTER - SAMPLE QUESTIONS PAPERSEXERCISE - QUESTION
157 Videos
- SIMPLE INTERESTBOOK - CALCUTTA BOOK HOUSECHAPTER - SIMPLE INTERESTEXERCISE - Long-answer type questions
37 Videos
Similar Questions
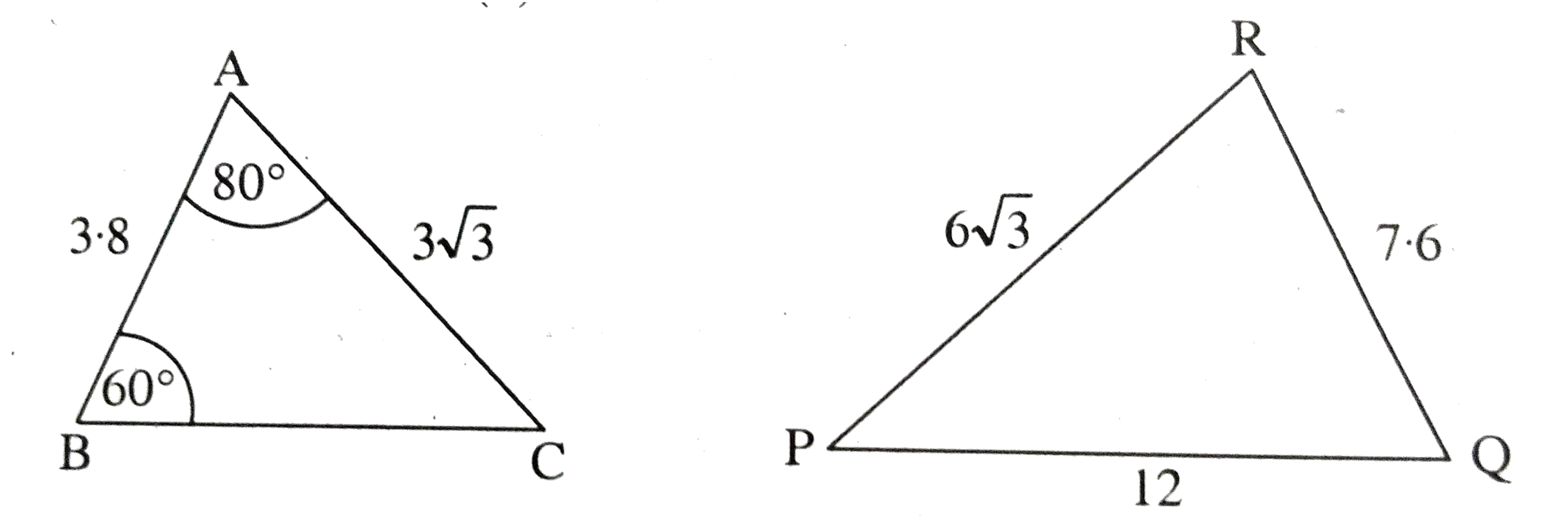
In the following figure , ∠P=
View SolutionA person deposite ₹ 100 in a bank and after 2 yars he got a total ₹121 as a return. Then the componund interest of the bank per annum is
View SolutionGoutam took a loan of some money from a cooperative bank for opening a poultry farm at the rate of simple interest of 12% per annum. Every month he has to repay 378Rs as interest. Determine the loan amount taken by him.
View SolutionThe sides of two similar triangles are 4 : 9 . What is the ratio of their area?
View SolutionThe perimeter of two similar triangles are in 4:9 ratio, the ratio of their corresponding sides is…………..
View SolutionThe ratio of the areas of two similar triangles is 1:4 then the ratio of their corresponding sides………….
View SolutionSides of two similar triangles are in the ratio 4 : 9 Areas of these triangles are in the ratio
View SolutionThe ratio of the area of two similar triangle is 4:5, the ratio of their corresponding sides are :
View SolutionSides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
View SolutionThe side of two similar triangles are 4:9. What is the ratio of their area?
View SolutionTick the correct answer and justify : Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
View SolutionSides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio___
View SolutionTick the correct answer and justify : Sides of two similar triangles are in the ratio 4:9. Areas of these triangles are in the ratio
View SolutionCalculate the ratio of the area of two similar triangles if the sides of the triangles are in the ratio of 9:4.
View SolutionThe ratio of areas of two similar triangles is 4:9. Then, the ratio of their sides is:
View Solution
