In an isosceles right-angled triangle ABC,∠B=90∘. The bisector of ∠BAC intersects the side BC at the point D. Prove that CD2=2BD2Solution in Bengali
Step by step video & image solution for In an isosceles right-angled triangle ABC,/_B=90^(@). The bisector of /_BAC intersects the side BC at the point D. Prove that CD^(2) =2BD^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREM BOOK - CALCUTTA BOOK HOUSECHAPTER - PYTHAGORAS THEOREM EXERCISE - EXAMPLE 6
4 Videos
- PYTHAGORAS THEOREM BOOK - CALCUTTA BOOK HOUSECHAPTER - PYTHAGORAS THEOREM EXERCISE - EXAMPLE 3
4 Videos
- PROBLEMS RELATED TO DIFFERENT SOLIDS AND OBJECTS BOOK - CALCUTTA BOOK HOUSECHAPTER - PROBLEMS RELATED TO DIFFERENT SOLIDS AND OBJECTS EXERCISE - Long - answer type questions (LA):
20 Videos
- QUADRATIC EQUATION IN ONE VARIABLEBOOK - CALCUTTA BOOK HOUSECHAPTER - QUADRATIC EQUATION IN ONE VARIABLEEXERCISE - EXERCISE-1.5
40 Videos
Similar Questions
A person at first travels 28m east from a certain place and then he travels √57m south of it. The distance of the person from the starting point will be
View SolutionIn the given figure,the point O is situated within the triangle PQR in such a way that, ∠POQ=90∘,OP=6cm and OQ=8cm. If PR= 24 cm and ∠QPR=90∘, then find the length of QR.
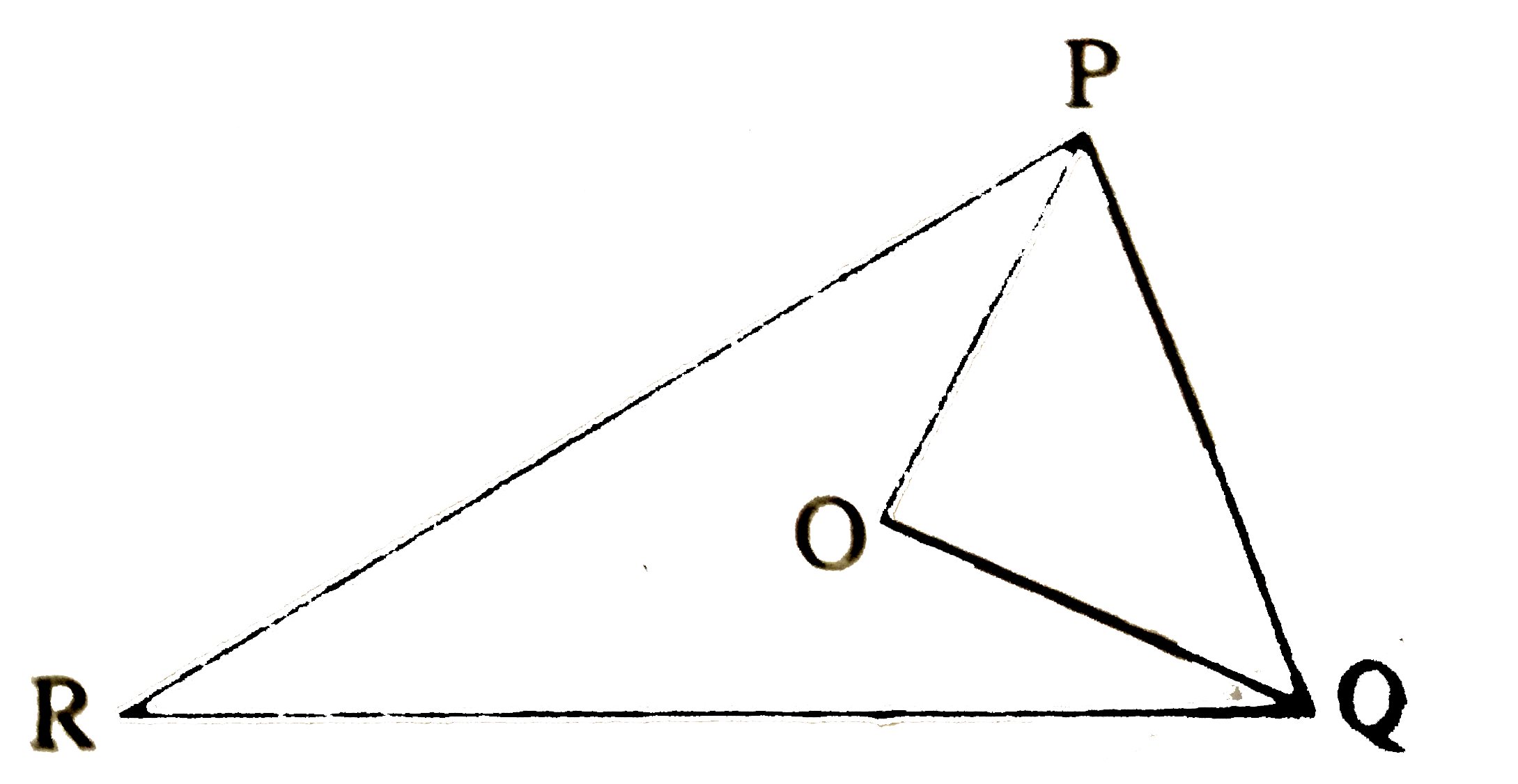
View SolutionA conical pot of internal radius 5 cm and height 24 cm is filled with water . It this water is poured into a right cylindrical pot of radius 10 cm , then what will be the height of water - level into the pot ?
View SolutionIf the roots of the quadratic equation x2−m(2x−5)−6=0 are equal, then m=
View SolutionABC is a triangle in which ∠B =2 ∠C.D is a point on BC such that AD bisects ∠BAC and AB=CD . Prove that ∠BAC=720.
View SolutionABC is a right angled isosceles triangle with /_B=90^(@) If D is a point on AB such that /_CDB=15^(@) and ifAD=35cm then CD is equal to
View SolutionABC is a triangle in which ∠B=2∠C.D is a point on BC such that AD bisects ∠BAC and AB=CD. Prove that ∠BAC=72∘
View SolutionABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है । यदि AB2=2AC2 है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है ।
View Solutionएक समद्विबाहु त्रिभुज ABC इस प्रकार है कि AC = BC यदि AB2=2AC2 है तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है |
View Solutionएक समद्विबाहु त्रिभुज ABC की भुजा AC पर बिंदु D इस प्रकार है की BC2=AC×CD|यदि AB =AD हो तो सिद्ध करो की BD =BC
View SolutionIf D be the mid-point of the side BC of ΔABC, then AB2+AC2=2BD2+"…..................".
View SolutionABC is a right triangle , right angled at A and D is the mid point of AB . Prove that BC2=CD2+3BD2 .
View Solutionএকটি সমদ্বিবাহু ত্রিভুজ ABC অঙ্কন করা হল যার ∠B সমকোণ । ∠BAC -এর সমদ্বিখন্ডক অঙ্কন করা হল যা BC বাহুকে D বিন্দুতে ছেদ করেছে । প্রমাণ করো যে, CD2=2BD2
View SolutionABC সমদ্বিবাহু ত্রিভুজের AB=AC এবং ∠BAC=90∘, ∠BAC-এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে ছেদ করে। প্রমাণ করো যে, sec∠ACDsin∠CAD=cosec2∠CAD
View SolutionD is a point on the side BC of a triangle ABC such that ∠ADC=∠BAC. Show that CA2=CB⋅CD.
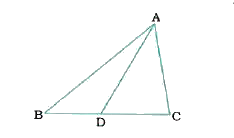
View Solution
