O is an internal point of the rectangle PQRS. Prove that OQ2+OS2=OP2+QR2Solution in Bengali
Step by step video & image solution for O is an internal point of the rectangle PQRS. Prove that OQ^(2)+OS^(2) = OP^(2) +QR^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREM BOOK - CALCUTTA BOOK HOUSECHAPTER - PYTHAGORAS THEOREM EXERCISE - EXAMPLE 6
4 Videos
- PYTHAGORAS THEOREM BOOK - CALCUTTA BOOK HOUSECHAPTER - PYTHAGORAS THEOREM EXERCISE - EXAMPLE 3
4 Videos
- PROBLEMS RELATED TO DIFFERENT SOLIDS AND OBJECTS BOOK - CALCUTTA BOOK HOUSECHAPTER - PROBLEMS RELATED TO DIFFERENT SOLIDS AND OBJECTS EXERCISE - Long - answer type questions (LA):
20 Videos
- QUADRATIC EQUATION IN ONE VARIABLEBOOK - CALCUTTA BOOK HOUSECHAPTER - QUADRATIC EQUATION IN ONE VARIABLEEXERCISE - EXERCISE-1.5
40 Videos
Similar Questions
A person at first travels 28m east from a certain place and then he travels √57m south of it. The distance of the person from the starting point will be
View SolutionIn the given figure,the point O is situated within the triangle PQR in such a way that, ∠POQ=90∘,OP=6cm and OQ=8cm. If PR= 24 cm and ∠QPR=90∘, then find the length of QR.
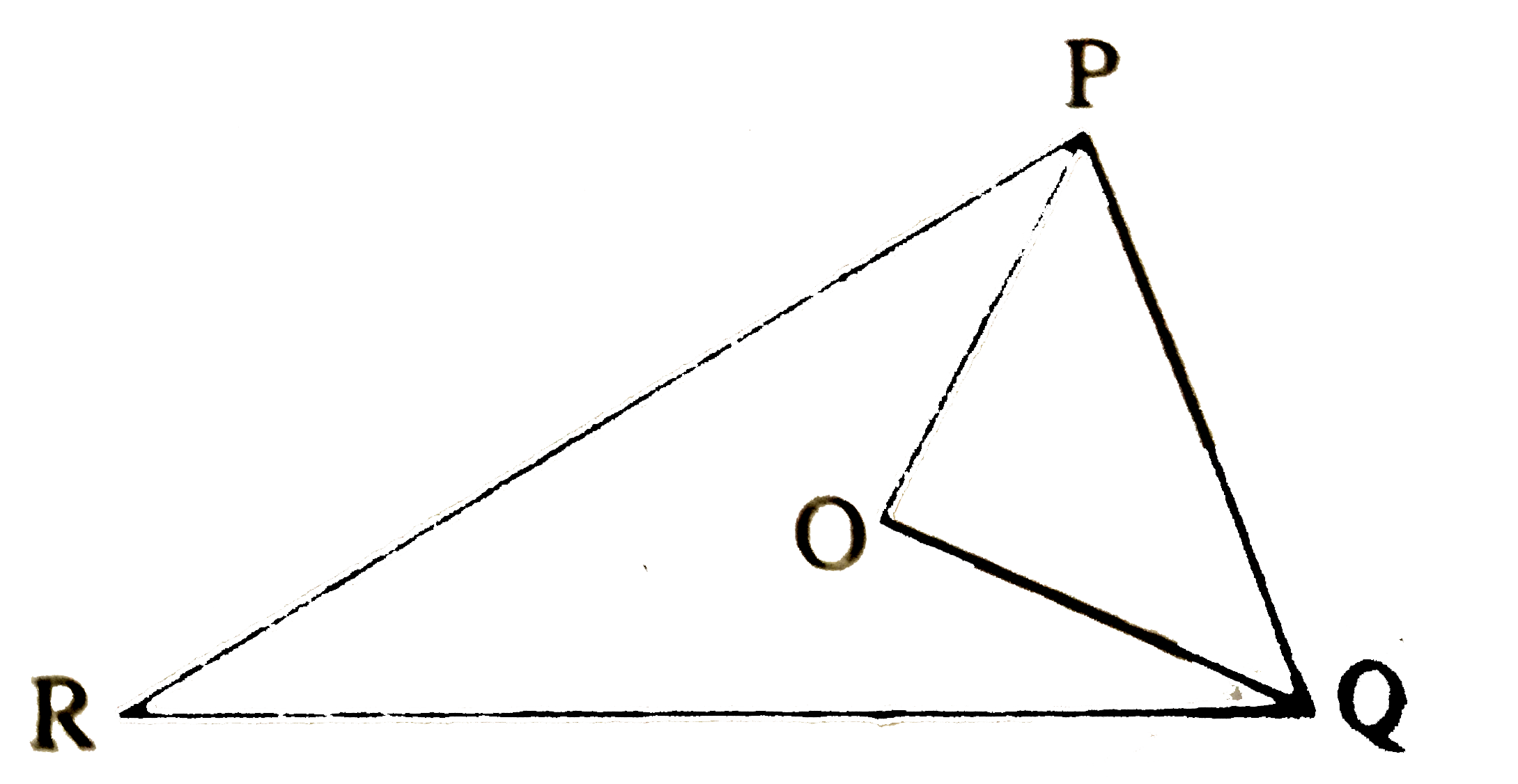
View SolutionA conical pot of internal radius 5 cm and height 24 cm is filled with water . It this water is poured into a right cylindrical pot of radius 10 cm , then what will be the height of water - level into the pot ?
View SolutionIf the roots of the quadratic equation x2−m(2x−5)−6=0 are equal, then m=
View SolutionTake any point O in the interior of a triangle PQR. Is (i) OP+OQ>PQ? (ii) OQ+OR>QR? (iii) OR+OP>RP?
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that bar(OP)*bar(OQ)+bar(OR)*bar(OS)=bar(OR)*bar(OP)+bar(OQ)*bar(OS)=bar(OQ)*bar(OR)+bar(OP)*bar(OS) Then the triangle PQR has S as its
View SolutionPQR is a triangle whose ∠Q is right angle. If S is any point on QR, then prove that PS2+QR2=PR2+QS2
View SolutionLet PQRS be a parallelogram whose diagonals PR and QS intersect at O'. If O is the origin, then (−−→OP+−−→OQ+−−→OR+−−→OS) is equal to -
View SolutionLet PQRS be a parallelogram whose diagonals PR and QS intersect at O'. IF O is the origin then : ¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR+¯¯¯¯¯¯OS=
View Solutionमाना कि O मुलबिन्दु है एवं PQR एक स्वेच्छिक त्रिभुज है | बिन्दु S इस प्रकार है कि
−−→OP.−−→OQ+−−→OR.−−→OS=−−→OR.−−→OP+−−→OQ.−−→OS=−−→OQ.−−→OR+−−→OP.−−→OS
तब बिन्दु S त्रिभुज PQR का है
View SolutionPQRSসামান্তরিকের PR ও QS কর্ণ দুটি O' বিন্দুতে ছেদ করে, যদি মূলবিন্দু O হয় তবে (−−→OP+−−→OQ+−−→OR+−−→OS)-এর মান হবে -
View SolutionDelta PQR There is a point O in the interior of. A, B and C are the midpoints of OP, OQ and OR respectively. Prove that Delta ABC And Delta PQR Will be isosceles.
View SolutionTake any point O in the interior of a triangle PQR. Is (i) OP+OQ>PQ? (ii) OQ+OR>QR? (iii) OR+OP>RP?
View Solutionमाना कि O मुलबिन्दु है एवं PQR एक स्वेच्छिक त्रिभुज है | बिन्दु S इस प्रकार है कि
−−→OP.−−→OQ+−−→OR.−−→OS=−−→OR.−−→OP+−−→OQ.−−→OS=−−→OQ.−−→OR+−−→OP.−−→OS
तब बिन्दु S त्रिभुज PQR का है
View SolutionDeltaXYZ in, angleY And angleZ The bisectors of point meet at point O respectively. OP bot YZ , OQ bot ZX And OR bot XY Prove that OP=OQ=OR
View Solution
