In ΔABC, m ∠BAC=90∘, seg DE⊥ side AB, seg DF⊥ side AC, seg AD⊥ side BC.
Prove : A(□AEDF)=√AE×EB×AF×FC)Solution in Tamil
The correct Answer is:∴A(□AEDF)=√AE×EB×AF×FC)
Step by step video, text & image solution for In DeltaABC," m "angleBAC=90^(@)," seg " DEbot" side "AB, " seg "DFbot" side "AC," seg "ADbot" side "BC. Prove : A(squareAEDF)=sqrt(AExxEBxxAFxxFC)) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHALLENGING QUESTIONSBOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Circle
9 Videos
- CHALLENGING QUESTIONSBOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Geometric Constructions
6 Videos
- CHALLENGING QUESTIONSBOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Similarity
9 Videos
- ARITHMETIC PROGRESSION BOOK - CHETAN PUBLICATIONCHAPTER - ARITHMETIC PROGRESSION EXERCISE - ASSIGENMENT -3
10 Videos
- CIRCLEBOOK - CHETAN PUBLICATIONCHAPTER - CIRCLEEXERCISE - Assignment - 3 (Solve any two of the following questions):
3 Videos
Similar Questions
From the end points of a diameter a diameter of circle perpendiculars are drawn to a tngent of the same circle. Show their feet on the tangent are equidistant from the centre of the circle.
View SolutionDraw a ΔABC with side BC=6 cm,∠B=45∘ and ∠A=100∘, then construct a triangle whose sides are 47 times the corresponding sides of ΔABC.
View SolutionBisector of ∠B and ∠C in ΔABC meet each other at P. Line Ap cuts the side BC at Q. Then prove that : APPQ=AB+BCBC

View SolutionWhat is the common difference (d) of the A.P. 2,-2,-6,-10….. ?
View SolutionA circle with centre 'O' is incircle of ΔABC.ΔBCA=90∘ . Radius of the circle is r.
Prove that : 2r = a + b - c.

View SolutionIn the figure, seg DE∣∣ side AC and seg EF∣∣ side BA then prove that ADDB×AFFC=1
View SolutionIn ΔABC, ∠ABC=90∘, AB=12, BC=16 and seg BP is the median drawn to side AC. Find the length of seg BP.
View SolutionIn ΔABC seg MN∣∣ side AC. Seg MN divides ΔABC into two parts equal in area. Determine MBAB.
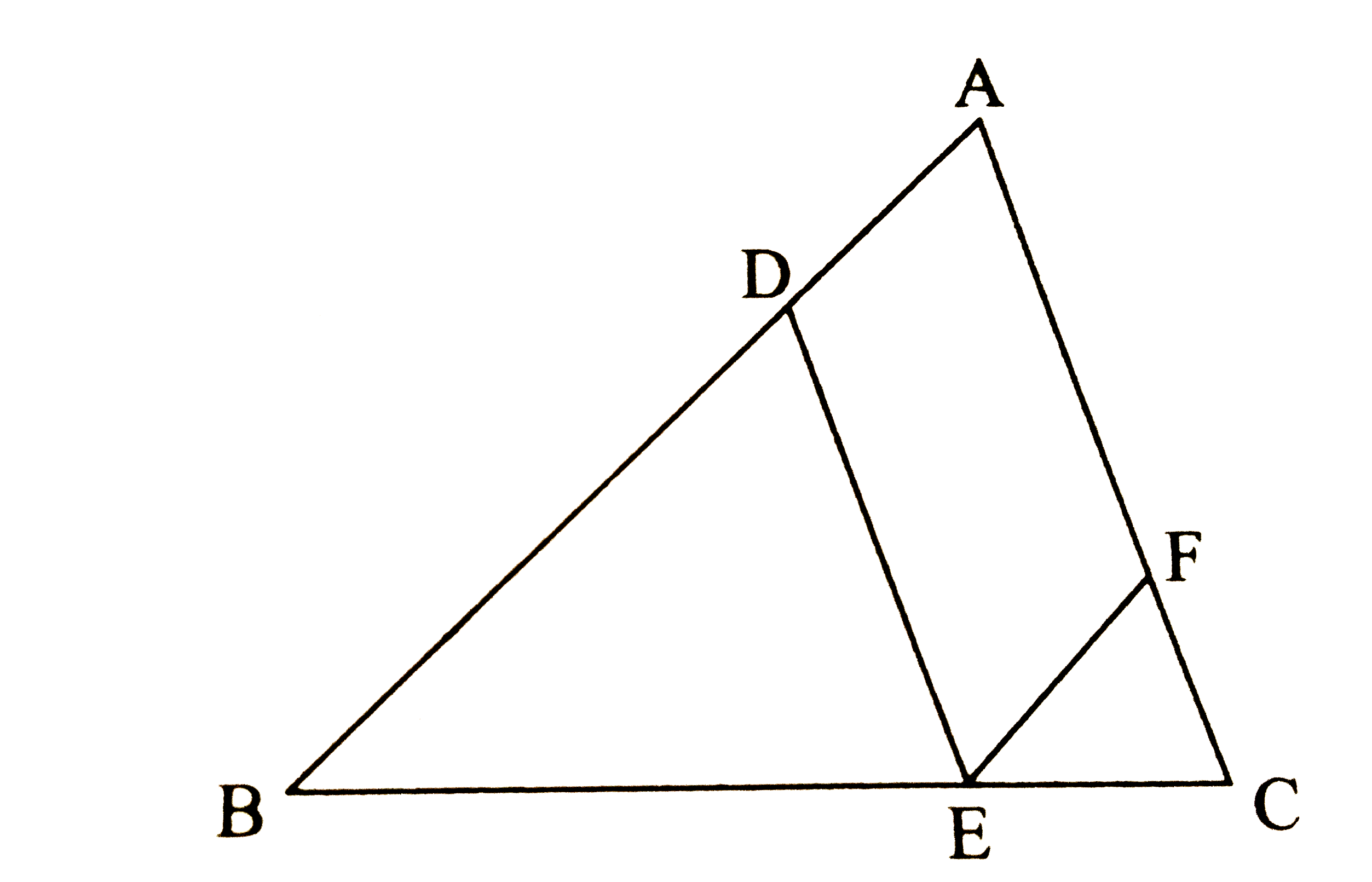
View SolutionIn the adjoining figure,seg DE||side AC and seg DC ||side AP.
Prove that BEEC=BCCP.
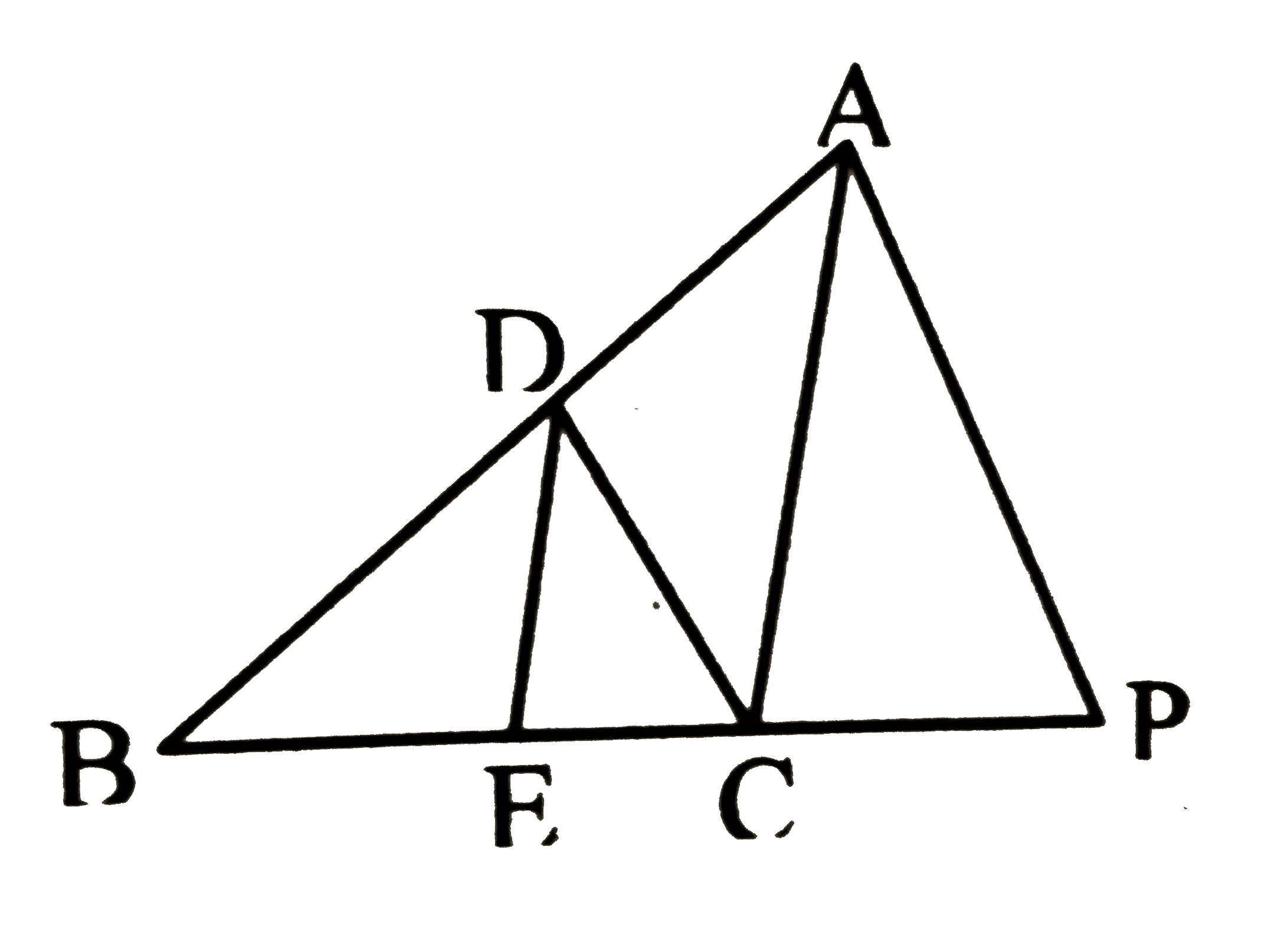
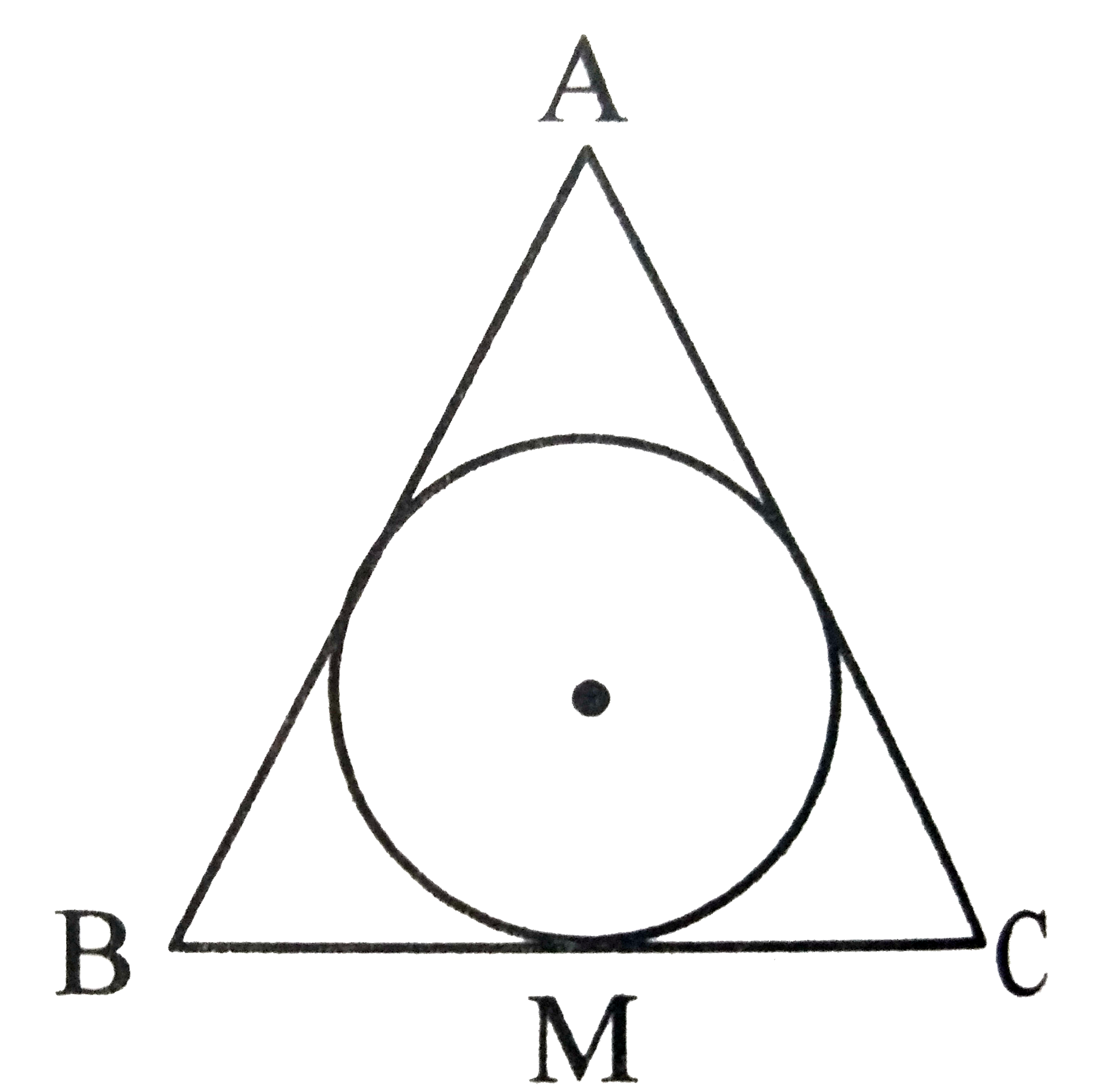
View SolutionIn the adjoining figure, the circle is the incircle of isosceles ΔABC, where seg AB=seg AC. Prove that M bisects BC.
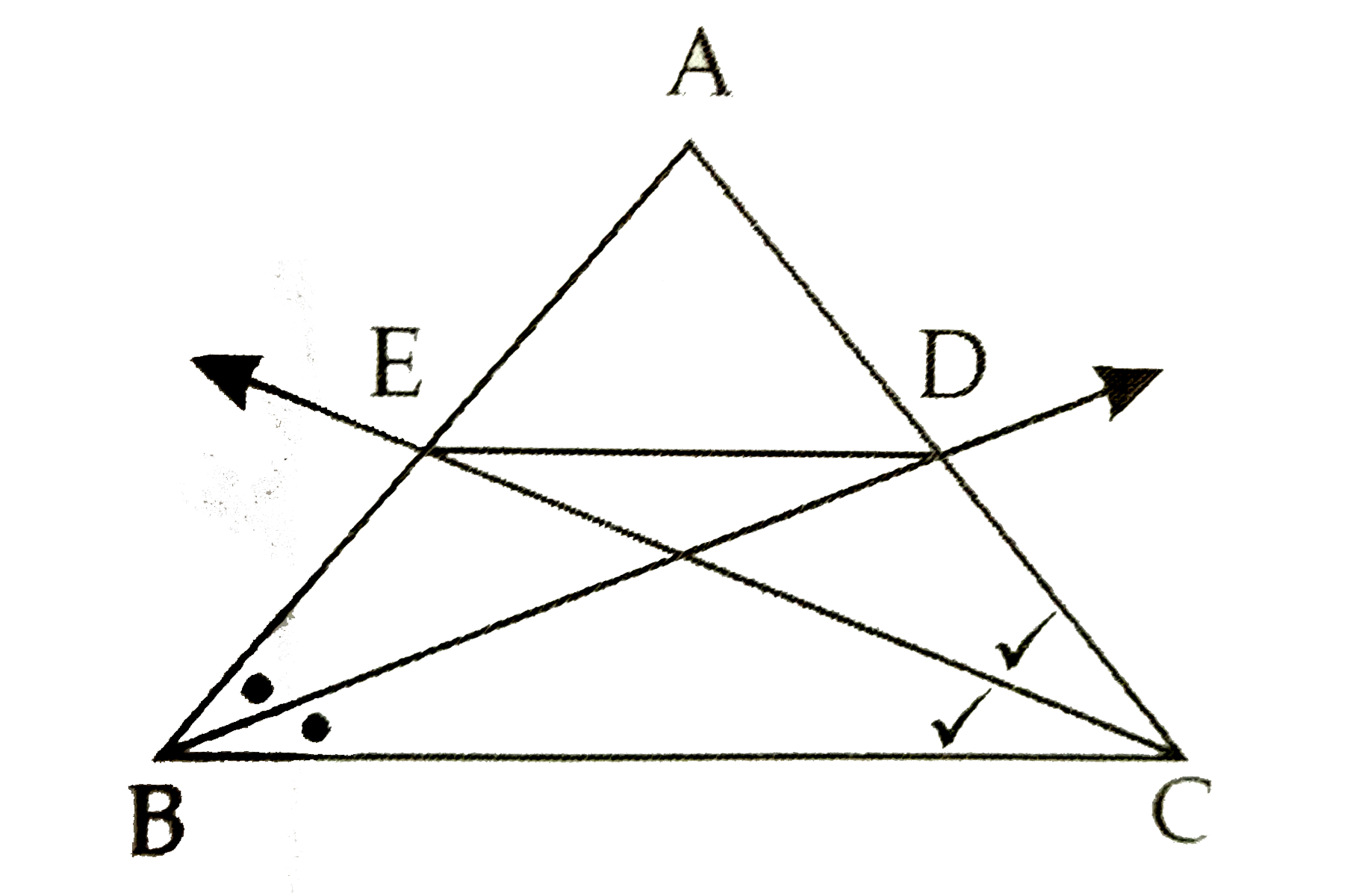
View SolutionIn ΔABC,seg BD bisects ∠ABCandRay CE bisects ∠ACB.if seg AB≅seg AC then prove that ED||BC.
View SolutionIn ΔABC,∠B=90∘,seg DE⊥side AC.AD=6,AB=12,AC=18, , then find AE.
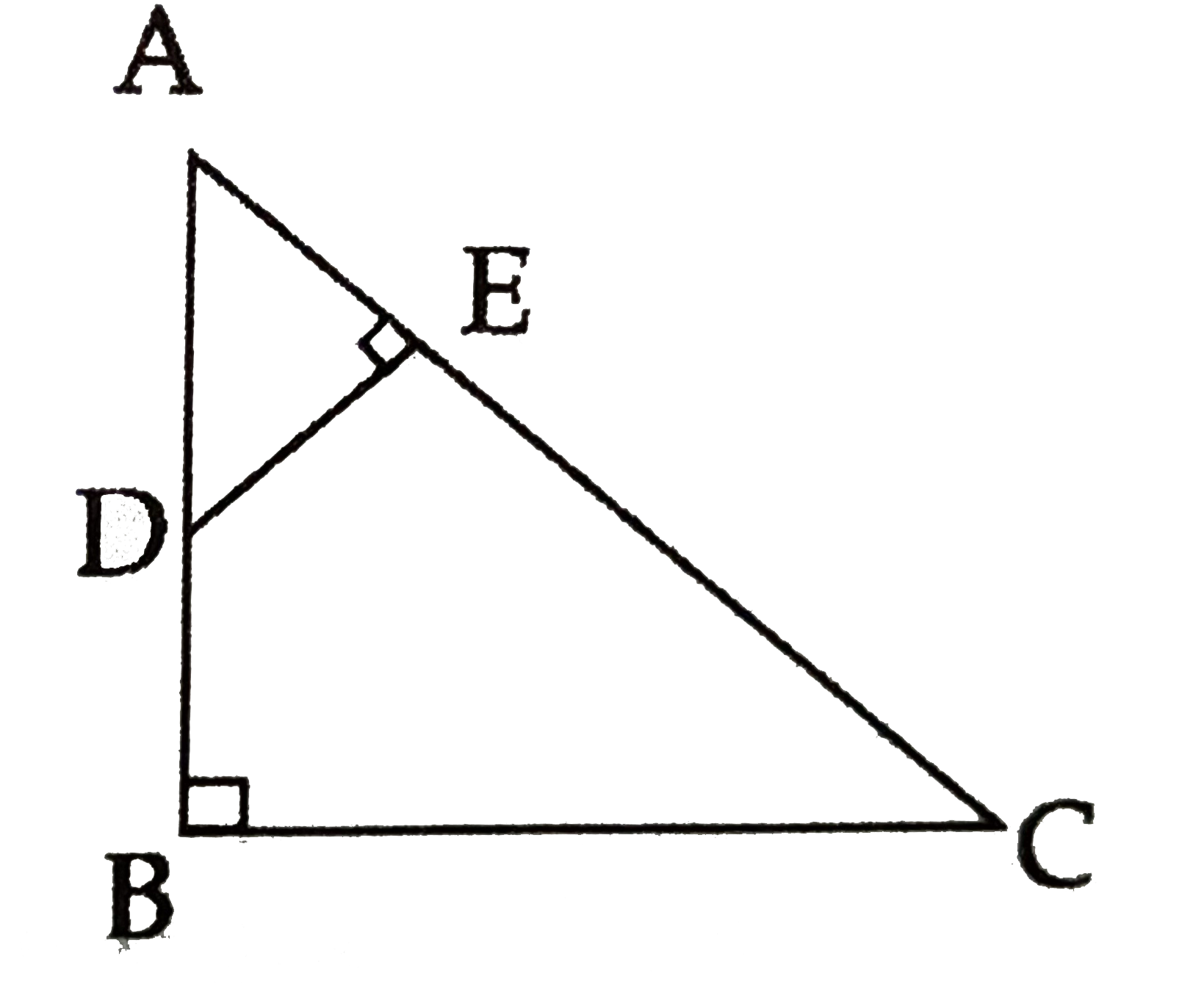
View SolutionE is a point on side CB,C−B−E,InΔABC,AB=AC.If seg AD,BC,B−D−CandsegEF⊥sideAC,A−F−C.Prove that ΔABD~ΔECF.
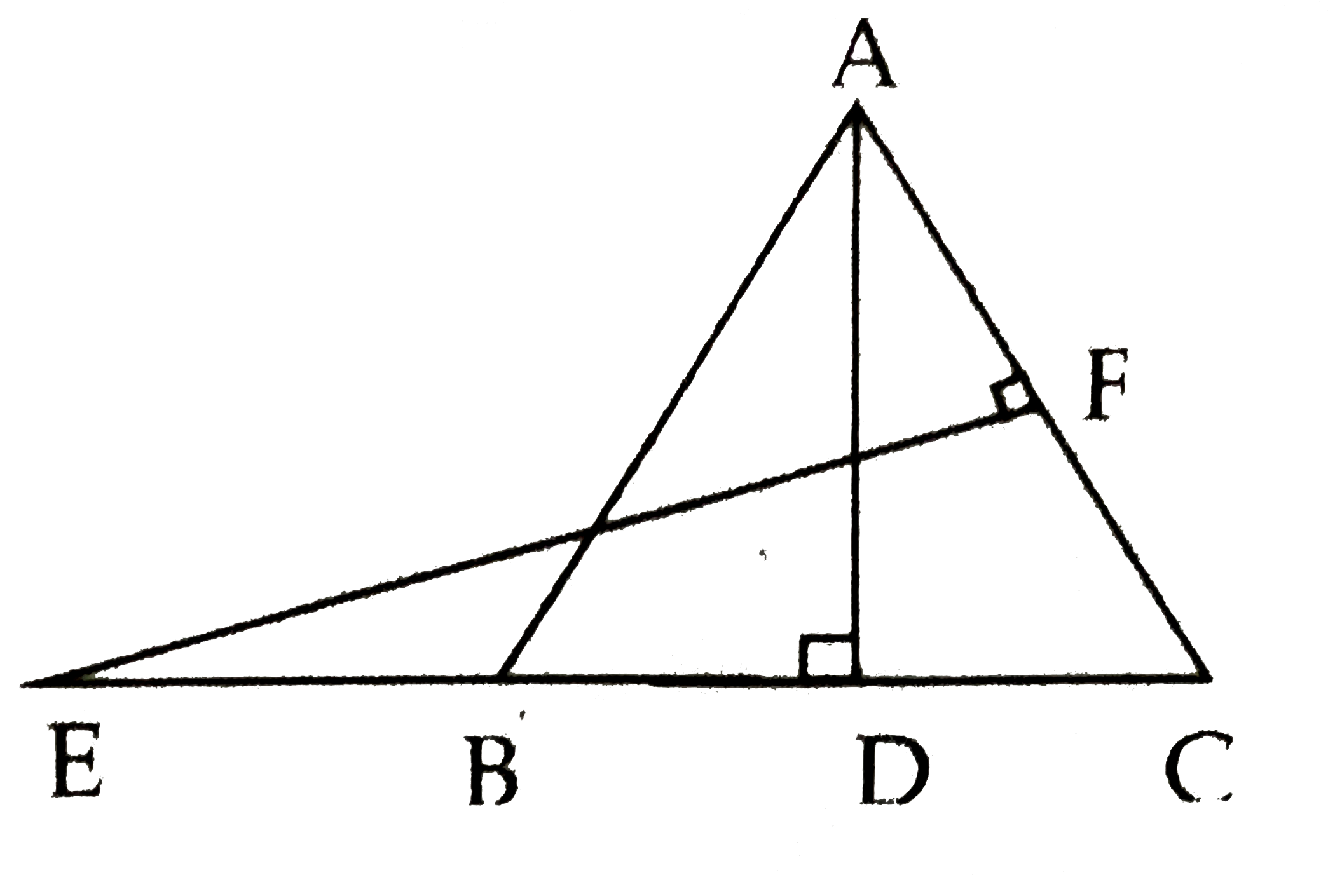
View SolutionIn the adjoining figure seg Ce⊥ side AB, segAD⊥ side BC. Prove that
(i) ΔAEP~ΔCDP
(ii)ΔAEP~ΔADB
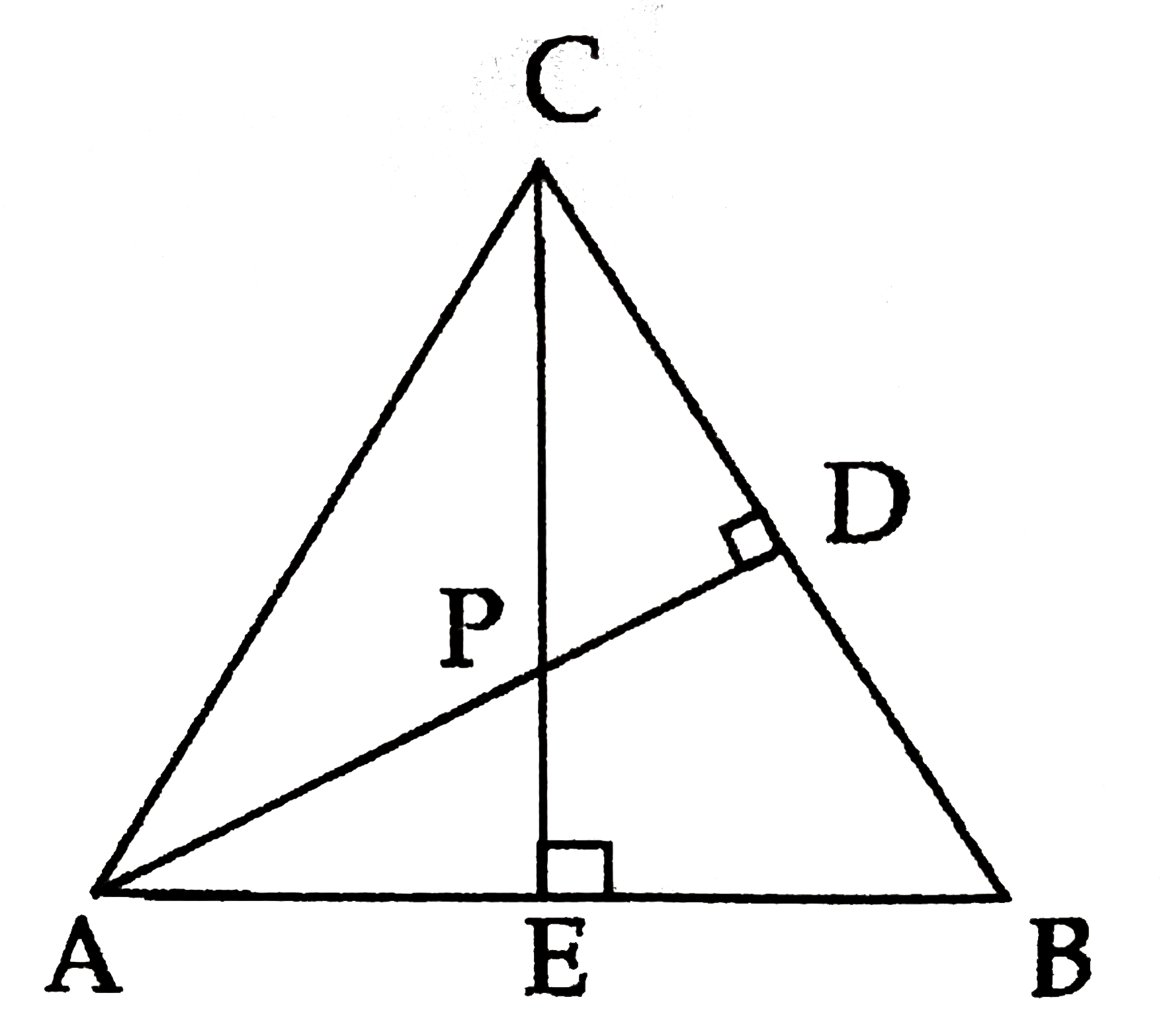
View SolutionLet X be any point on side BC of ΔABC seg XM || side AB and seg XN ||side CA . M - N- T , T - B - X . Prove that : TX2=TB.TC.
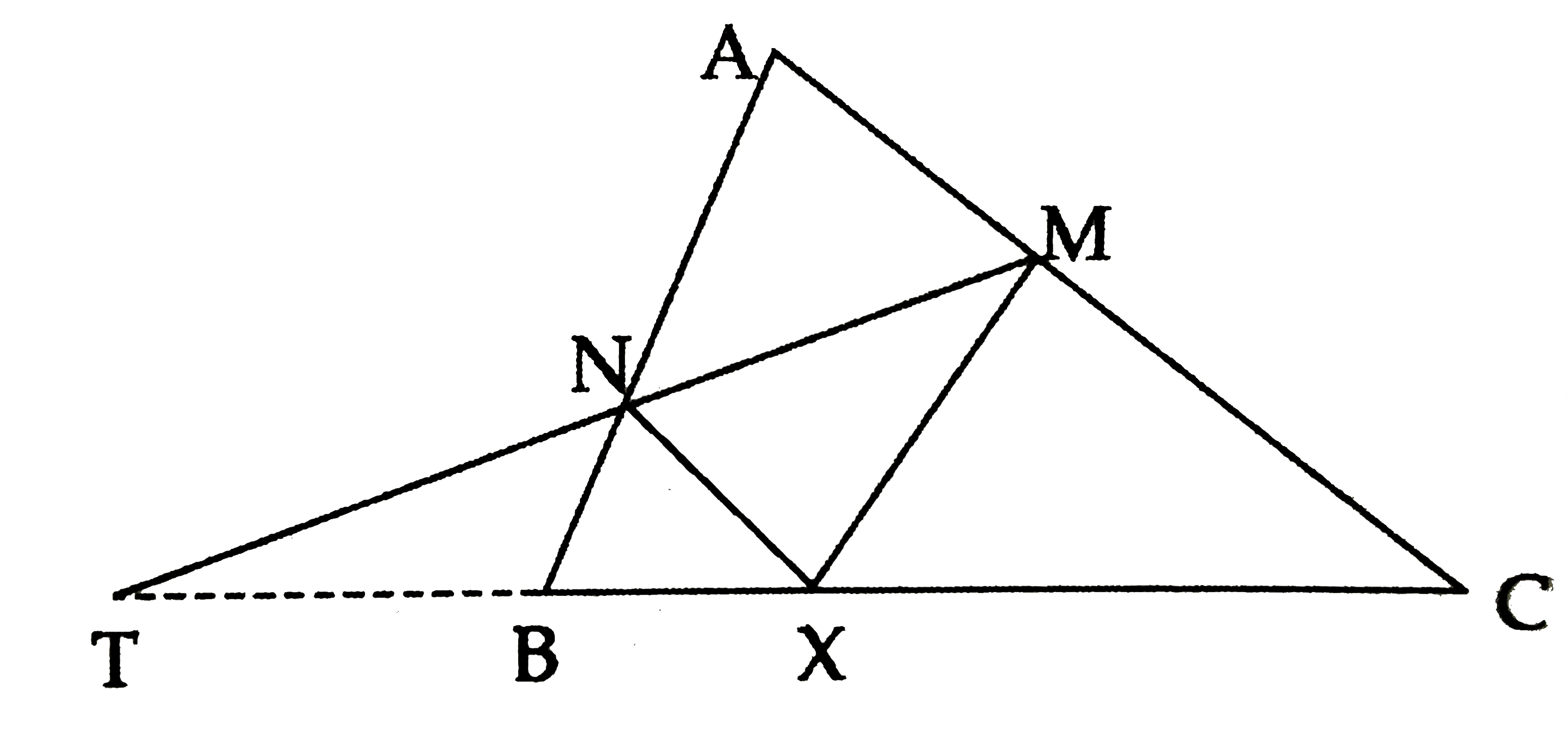
View Solution
