Question

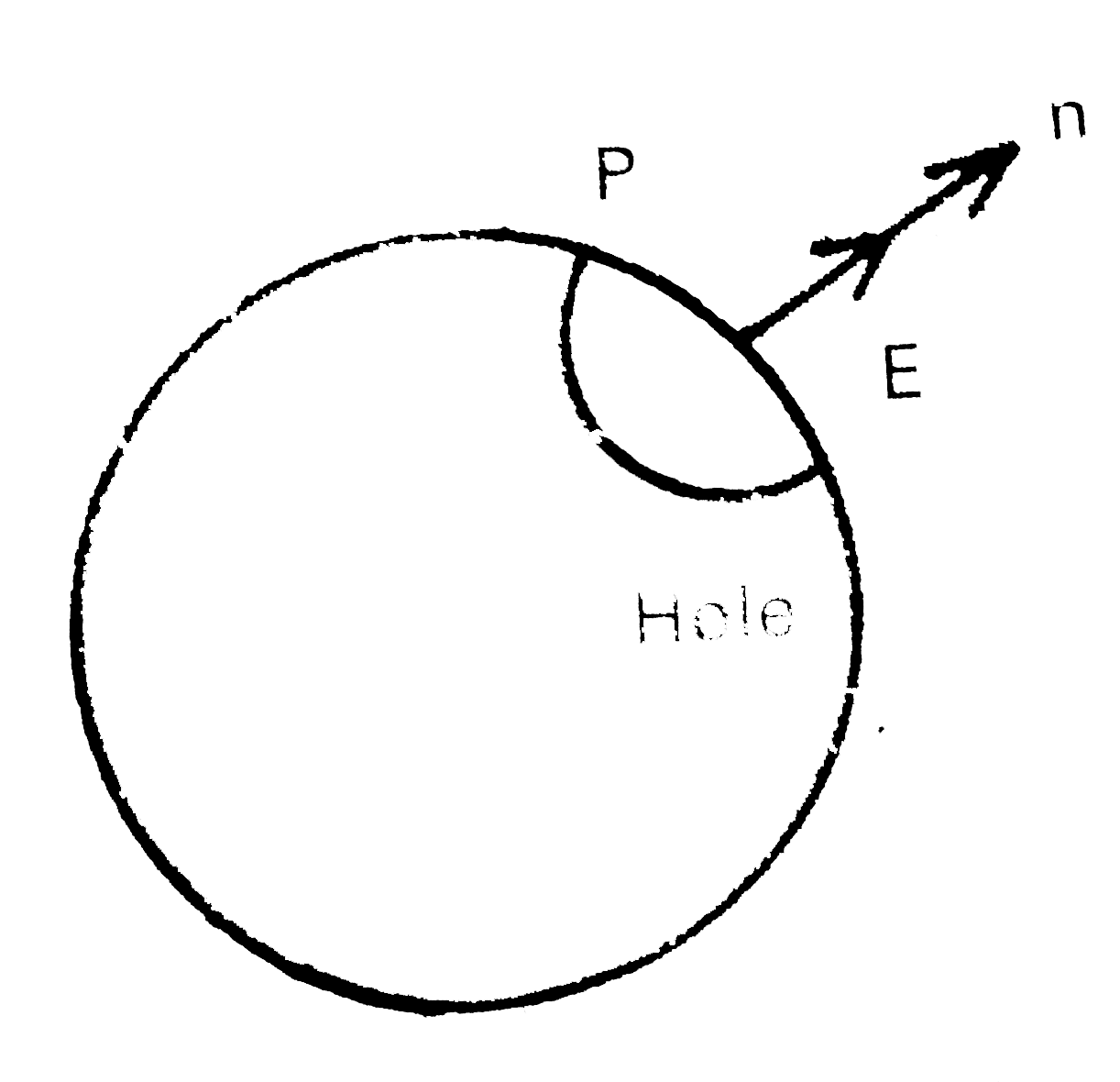
A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is $(\sigma /\epsilon {\epsilon }_0)\hat{n}$, where $\hat{n}$ is the unit vector in the outward normal direction and $\sigma$ is the surface charge density near the hole.

Explanation

Surface charge density near the hole `=sigma`
Unit vector `=hat(n)` (normal directed outwards)
Let P be the point on the hole
the electric field at point P closed to the surface of conductor, according to Gauss's theorem,
`oint E.dS=q/epsi_(0)`
where q is the charge near the hole.
`E ds cos theta=(sigma dS)/epsi_(0)( :' sigma =q/(dS) :. q =sigma dS)` where `dS =` area
`:'` Angle between electric field and area vector is `0^(@)`.
`EdS=(sigma dS)/epsi_(0)`
`E=sigma/epsi_(0)`
`E=sigma/epsi_(0) hat(n)`
This electric field is due to the filled up hole and the field due to the rest of the charged conductor. The two fields inside the conductor are equal and opposite. So, there is no electric field inside the conductor. Outside the conductor, the electric fields are equal and area in the same direction.
So, the electric field at P due to each part `=1/2 E=sigma/(2 epsi_(0)) hat(n)`