Obtain the formula for the electric field due to a long thin wire of uniform linear charge density $λ$ without using Gauss's law.

Text Solution

Verified by Experts

Let us consider a long thin wire of linear charge density $λ$ . We have to find the resultant electric field due to this wire at point P.
Now, consider a very small element of length dx at a distance x from C.

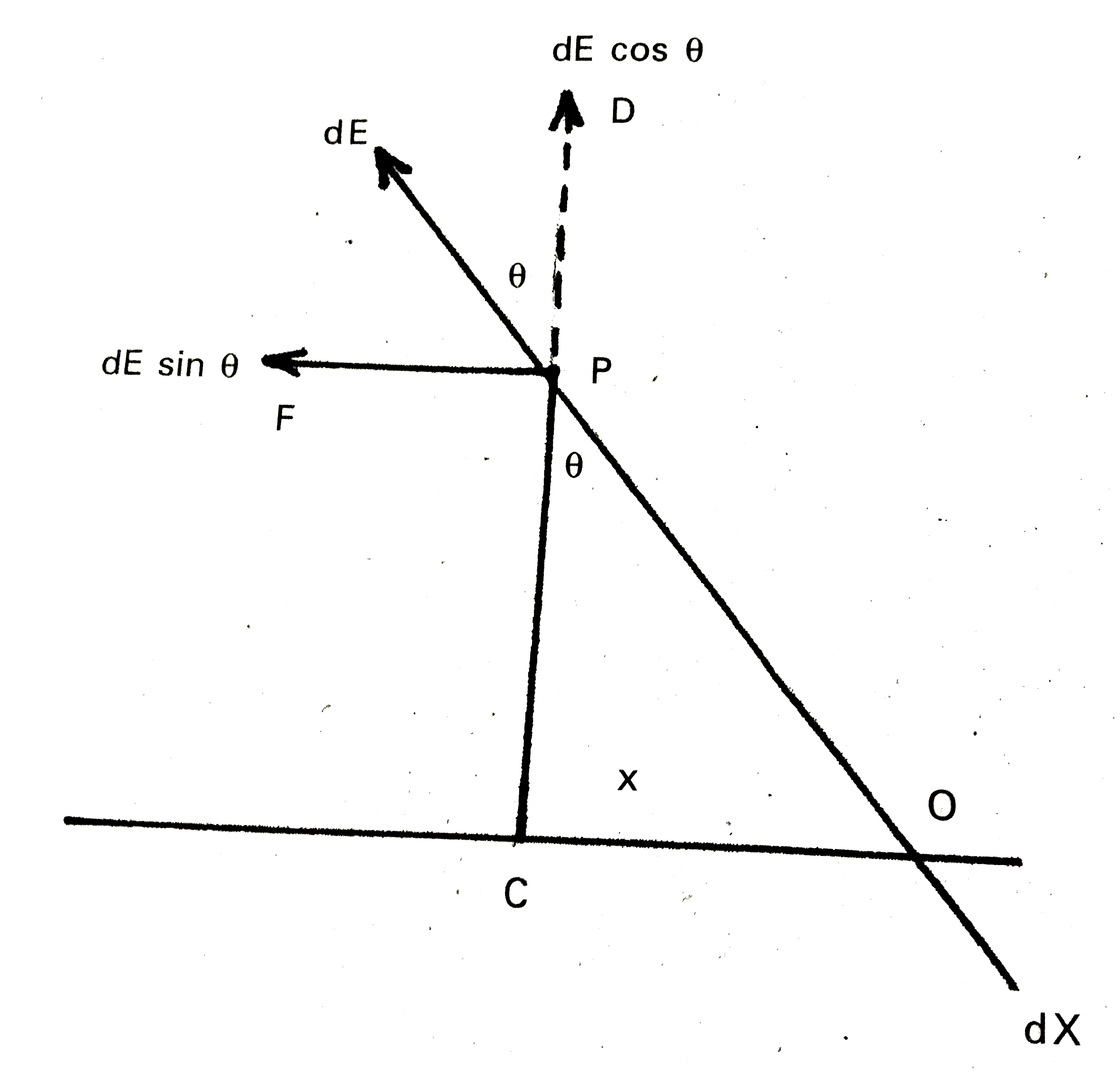
The charge on this elementary portion of length dx
$q = λ d x$ ...(1)
Electric field intensity at point P due to the elementary portion
$d E = \frac{1}{4 π ε_{0}} . \frac{q}{{(O P)}^{2}} = \frac{1}{4 π ε_{0}} \frac{λ d x}{{(O P)}^{2}}$ [ $∵$ from (1)]
Now, in $Δ P C O {(P O)}^{2} = {(P C)}^{2} + {(C O)}^{2}$
${(O P)}^{2} = r^{2} + x^{2}$
$d E = \frac{1}{4 π ε_{0}} \frac{λ d x}{(x^{2} + r^{2})}$ ...(2)
The components of dE are $d E cos θ$ along PD and $d E sin θ$ along PF.
Here, there are so many elementary portion. So all the $d E sin θ$ components balance each other. the resultant electric field at P is due to only $d E cos θ$ components.
The resultant electric field due to elementary component, $d E' = d E cos θ$
$d E' = \frac{1}{4 π ε_{0}} . \frac{λ d x}{(x^{2} + r^{2})} cos θ$ ...(3)
In $Δ O C P tan θ = \frac{x}{r} \Rightarrow x = r tan θ$
Differentiation with respect to $θ$ , we get
$d x = r {sec}^{2} θ d θ$
Putting in equation (3), we get
$d E' = \frac{1}{4 π ε_{0}} \frac{λ . r {sec}^{2} θ d θ cos θ}{(r^{2} + r^{2} {tan}^{2} θ)}$
$d E' = \frac{1}{4 π ε_{0}} \frac{λ . r {sec}^{2} θ d θ cos θ}{r^{2} {sec}^{2} θ}$
$d E' = \frac{1}{4 π ε_{0}} . \frac{λ}{r} cos θ d θ$
As the wire os of infinite length, so integrate within the limits $- \frac{π}{2}$ to $\frac{π}{2}$ , we get
$E' = \int d E' = \frac{1}{4 π ε_{0}} \frac{λ}{r} π / 2 \int - π / 2 cos θ d θ$
$E' = \frac{1}{4 π ε_{0}} . \frac{λ}{r} {[sin θ]}_{- π / 2}^{π / 2} = \frac{1}{4 π ε_{0}} \frac{λ}{r} [sin \frac{π}{20} sin (- \frac{π}{2})]$
$E' = \frac{1}{4 π ε_{0}} \frac{λ}{r} [1 + 1]$
$E' = \frac{2 λ}{4 π ε_{0} r}$
$∴ E' = \frac{λ}{2 π ε_{0} r}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The electric field intensity due to a thin infinity long straight wire of uniform linear charge density $λ$ at O is-

A $\frac{λ}{2 π ε_{0} R}$
B $\frac{λ \sqrt{2}}{2 π ε_{0} R}$
C $\frac{λ \sqrt{5}}{2 π ε_{0} R}$
Dzero

VIKRAM PUBLICATION ( ANDHRA PUBLICATION)-ELECTRIC CHARGES AND FIELDS-ADDITIONAL EXERCISES

Home
Ask Doubt
Profile