A nonumiform but spherically symmetric distribution of charge has charge density ∝ given as follow -
∝=∝0(1−r/R) for prop le R lt brgt ∝=0for r≤R
where ∝0=3Q/πR3 is a constant
( a) Show that the total charge contained in the charge distrubution is Q.
(b) Show that , for the region defined by r≤R, the electric field is identical to that produced by a point charge Q.
Obtain an expression for the electric field in the region r≤R.
(d) Compare your results in part (b) and (c ) r=R.
The correct Answer is:(c ) (kQr/R2)(4−3r/R)
(a) For total charge
q=∫ρdv⇒q=∫ρ0(1−rR)(4πr2dr)=ρx0
4π∫R0(r2−r3R)dr
q=ρ04π[R33−R44R]=ρ4π[R312] …(1)
put ρ0=3QπR3 in equation (1)
q=3QπR3×πR33=Q
(b) From gauss theorem for r≤R
r≤R∮→E.s→S=∑qɛ0E(4πr2)=∑qɛ0
Since sinq=Q for r≤R so E=14π∈0Qr2
(c) E=∑q4πɛ0r2 ...(1)
∑q=∫ρdV=∫r0ρ4πrder=ρ0×4π∫r0r2−r3Rdr
=3QπR2×4π[r23−r24R]
q=12QR2(r33−r44R) ...(2)
Sub. (2) in (1)
E=12Q4πɛ0r2×R3(r33−R44R)=KQrR3(4−3rR)
(d) In (b) r=R⇒E=KQR2 in ( c) r=R⇒E=KQR2.
Similar Questions
Consider a spherical symmetric charge distribution with charge density varying as ρ={[ρ0(1−rR),r≤R][0,,r>R]}The electric field at r ,r≤R will be
View Solution[" Consider a spherical symmetric "],[" charge distribution with charge "],[" density varying as "],[[rho={[rho_(0)(1-(r)/(R)),r<=R],[0],r>R]]
View Solution
Knowledge Check
In a region of space having a spherically symmetric distribution of charge, the electric flux enclosed by a concentric spherical Gaussian surface, varies with radius r as
ϕ=ϕ0r3R3 for r≤R
ϕ=ϕ0 for r > R
where R and ϕ0 are constants.
The volume charge density in the region is given asA3ϕ0ε0r24πε0R5 for r≤R,0 for r gt RB3ϕ0ε04πR3 for r≤R, 0 for r gt RCϕ0ε04πR2r for r≤R, 0 for r gt RD3ϕ0ε0πR3 for r≤R , 0 for r gt RIn a spherical distribution , the charge density varies as ρ(r)=A/r for a<r<b (as shown) where A is constant . A point charge Q lies at the centre of the sphere at r = 0 . The electric filed in the region a<r<b has a constant magnitude for
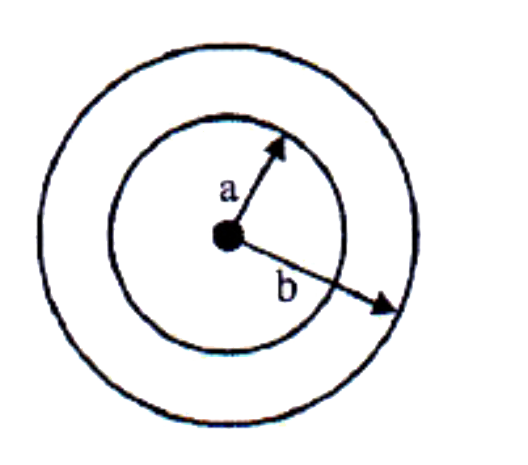 AA = 0BA = QCA=Q2Πa2DA=Q4Πa2
AA = 0BA = QCA=Q2Πa2DA=Q4Πa2
A solid ball of radius R has a charge density ρ given by ρ=ρ0(1−rR)for0≤r≤R The electric field outside the ball is :
View SolutionA solid ball of radius R has a charge density ρ given by ρ=ρ0(1−rR)for0≤r≤R The electric field outside the ball is :
View SolutionA spherical region of space has a distribution of charge such that the volume charge density varies with the radial distance from the centre r as ρ=ρ0r3,0≤r≤R where ρ0 is a positive constant. The total charge Q on sphere is
View SolutionA sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The electric field inside the sphere is
View SolutionIn a spherical distribution , the charge density varies as ρ(r)=A/r for a<r<b (as shown) where A is constant . A point charge Q lies at the centre of the sphere at r = 0 . The electric filed in the region a<r<b has a constant magnitude for

View SolutionFor spherical symmetrical charge distribution, variation of electric potential with distance from centre is given in diagram Given that : V=q4πε0R0 for r≤R0andV=q4πε0r for r≥R0
Then which option (s) are correct :
(1) Total charge within 2R0 is q
(2) Total electrosstatic energy for r≤R0 is non-zero
(3) At r=R0 electric field is discontinuous
(4) There will be no charge anywhere except at r<R0

View Solution
