A solid ball of radius R has a charge density ρ given by ρ=ρ0(1−rR)for0≤r≤R The electric field outside the ball is :
3ρ0R34ε0r2
ρ0R3ε0r2
ρ0R312ε0r2
4ρ0R33ε0r2
To find the electric field outside a solid ball of radius R with a given charge density ρ=ρ0(1−rR) for 0≤r≤R, we will follow these steps:
Step 1: Determine the total charge Qtotal
The total charge Qtotal can be calculated by integrating the charge density over the volume of the sphere. The charge density is given as:
ρ=ρ0(1−rR)
The volume element in spherical coordinates is:
dV=4πr2dr
Thus, the total charge is:
Qtotal=∫R0ρdV=∫R0ρ0(1−rR)4πr2dr
Step 2: Set up the integral
Substituting ρ into the integral:
Qtotal=4πρ0∫R0(1−rR)r2dr
Step 3: Simplify the integral
Distributing r2:
Qtotal=4πρ0(∫R0r2dr−1R∫R0r3dr)
Calculating the integrals:
∫R0r2dr=R33,∫R0r3dr=R44
Substituting these results back into the equation:
Qtotal=4πρ0(R33−1R⋅R44)
Step 4: Combine the terms
Qtotal=4πρ0(R33−R34)
Finding a common denominator (12):
Qtotal=4πρ0(4R312−3R312)=4πρ0⋅R312=4πρ0R312=πρ0R33
Step 5: Calculate the electric field outside the ball
For points outside the sphere (at a distance r from the center where r>R), the electric field E can be calculated using Gauss's law:
E=Qtotal4πϵ0r2
Substituting Qtotal:
E=πρ0R334πϵ0r2=ρ0R312ϵ0r2
Final Answer
The electric field outside the ball is:
E=ρ0R312ϵ0r2
---
Topper's Solved these Questions
Similar Questions
Consider a solid sphere oF radius R and mass density ρ(r)=ρ0(1−r2R2) 0<r≤R. The minimum density oF a liquid in which it will Float is:
View SolutionA ball of radius R carries a positive charges whose volume density at a point is given as ρ=ρ0(1−r/R), Where ρ0 is a constant and r is the distance of the point from the center. Assume the permittivities of the ball and the enviroment to be equal to unity.
(a) Find the magnitude of the electric field strength as a function of the distance r both inside and outside the ball.
(b) Find the maximum intensity Emax and the corresponding distance rm.View SolutionThe current density is a solid cylindrical wire a radius R, as a function of radial distance r is given by J(r)=J0(1−rR) . The total current in the radial regon r = 0 to r=R4 will be :
View SolutionA solid sphere of radius R1 and volume charge density ρ=ρ0r is enclosed by a hollow sphere of radius R2 with negative surface charge density σ, such that the total charge in the system is zero . ρ0 is positive constant and r is the distance from the centre of the sphere . The ratio R2/R1 is
View SolutionA solid non-conduction cylinder of radius R is charge such that volume charge density is proporation to r where r is distance from axis. The electric field E at a distance r(r<R) well depend on r as.
View SolutionA sphere of radius R has a variable charge density ρ(r)=ρ0rn−1(r≤R). If ratio of "potential at centre" and "potential at surface" be 3/2 then find the value of n
View SolutionAn infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
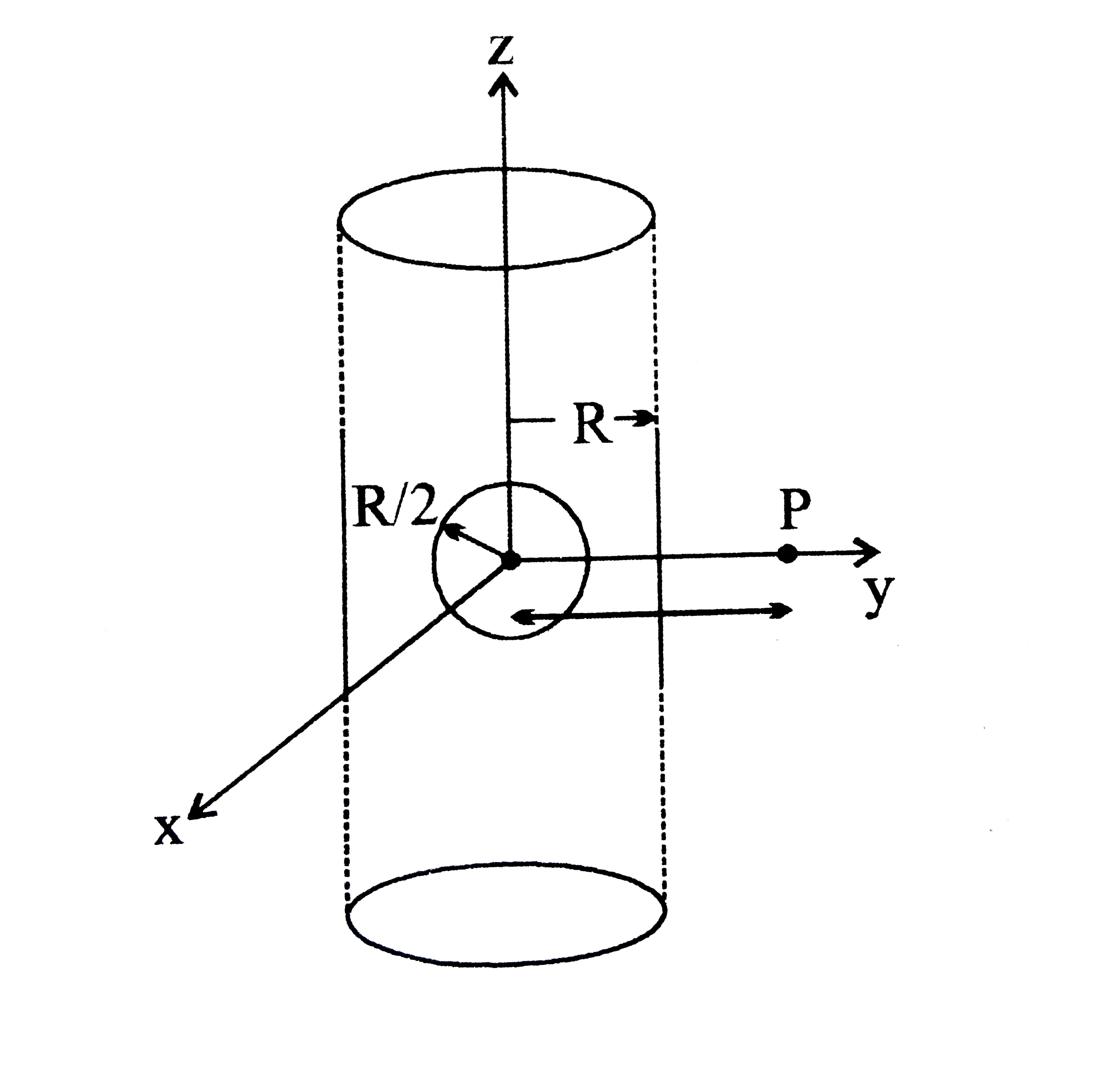 .View Solution
.View SolutionThe mass density of a planet of radius R varie with the distance r form its centre as ρ(r)=p0(1−r2R2). Then the graviational field is maximum at :
View SolutionA ring of radius R is placed in the plane its centre at origin and its axis along the x-asis and having uniformly distributed positive charge. A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velcity , then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represent by :
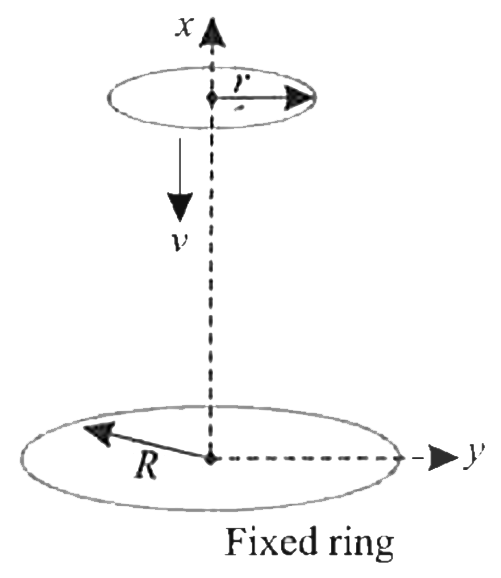 View Solution
View SolutionFigure shows a uniformly charged hemisphere of radius R. It has a volume charge density ρ. If the electric field at a point 2R, above the its center is E, then what is the electric field at the point 2R below its center?
 View Solution
View Solution

