A ring of mass M and radius R sliding with a velocity v0 suddenly enters inthrough surface where the coefficient of friction is μ, as shown in figure.
 .
.
Choose the correct statement (s).
The linear distance moved by the centre of mass before the ring starts rolling is 3v208μg
The net work done by friction force is −38mv20
The loss is kinetic energy of the ring is mv204
The gain in rotational kinetic energy is +mv208.
The correct Answer is:A, C, D
(A) v2=v20−2as at pure rolling v=v02
(V02)2=v20−2μgs⇒s=3v208μg
(B) Wfriction=ΔK⇒Wfriction=Kf−Ki
Wfriction=12m(v02)2(1+K2R2)−12mv20
Wfriction=12mv204(1+1)−12mv20
Wfriction=12mv20[12−1]⇒Wfriction=−14mv20
( C) Wfriction=ΔK,ΔK=14mv20
(D) KErotational=12Iω2
KErotational=12mR2×(v0/2R)2
Krotational=mv208.
Similar Questions
A disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionA cubical block of mass m is sliding on an inclined right angle trough as shown in the figure. If coefficient of friction is μ , find the acceleration of the block.
View Solution
Knowledge Check
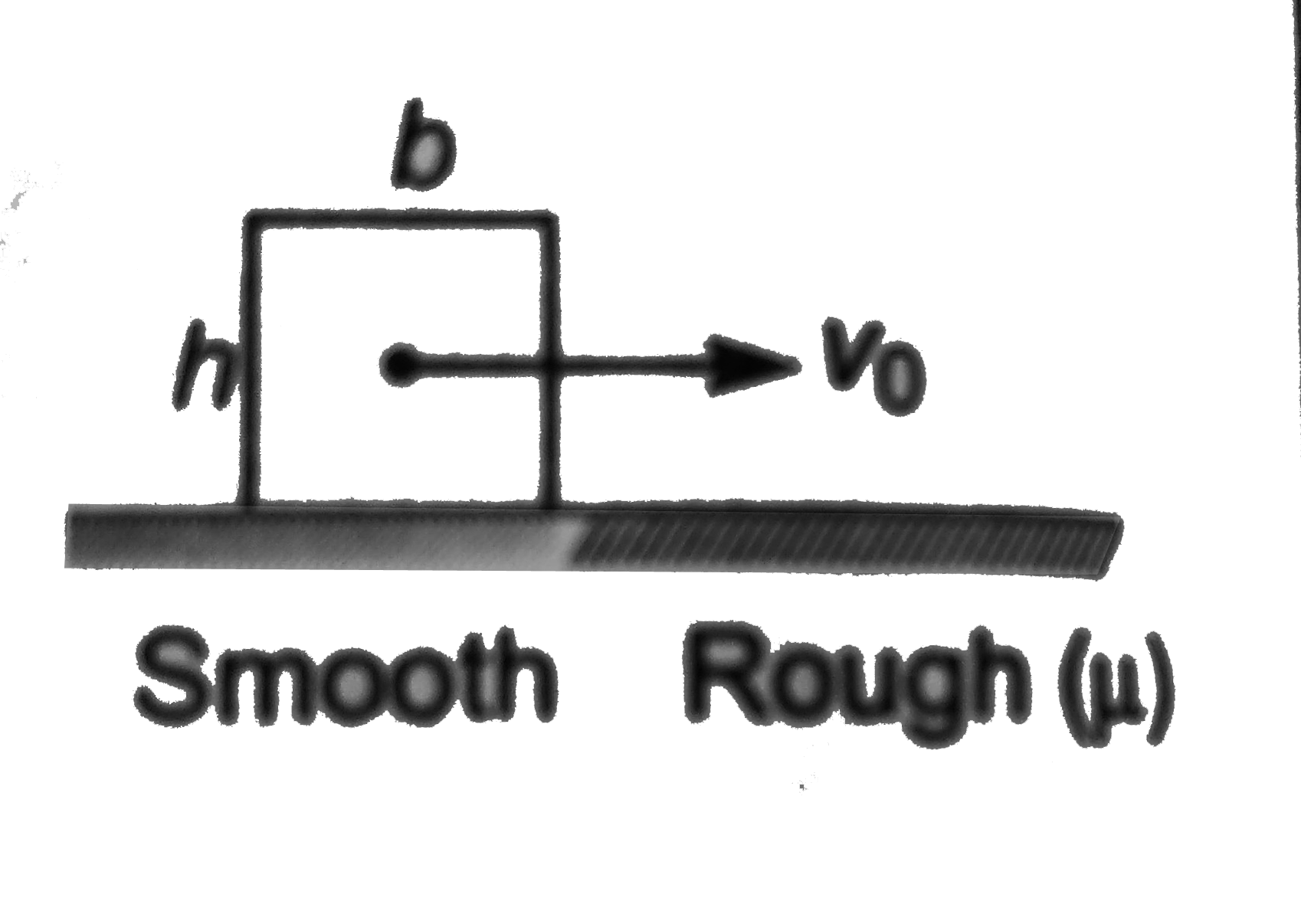
A rectangular block of size (×h) moving with velocity v0 enters on a rough surface where the coefficient of friction is μ as shown in figure. Identify the correct statement.AThenet torque acting on the block about its COM is μmg(h)2 (clockwise)Bthe net torque acting on the block about its COM is zeroCThe net torque acting on the block about its COM is in the anticlockwise senseDNone of the above.A ring of mass m sliding on a smooth surface with velocity v0 enters rough surface with coefficient of kinetic friction μk, then
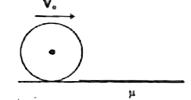 Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208
Athe linear distance moved by centre of mass before the ring starts pure rolling is 3v208μkgBthe gain in kinetic energy is mv208Cthe loss in kinetic energy is mv204Dthe work done by friction force is −3mv208A solid cylinder of mass M and radius R pure rolls on a rough surface as shown in the figure. Choose the correct alternative (s).
 AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3
AThe acceleration of the centre of mass is FMBThe acceleration of the centre of mass is 23FMCThe friction force on the cylinder acts backwardDThe magnitude of the friction force is F3
A sphere of mass M and radius R is moving on a rough fixed surface, having coefficient of friction μ. as shown in Fig. It will attain a minimum linear velocity after time v0>ω0R)

View SolutionA sphere of mass m is rolling without sliding along positive x-axis on a rough horizontal surface of coefficient of friction μ. It elastically collides with a wall and then returns. The correct statement of frictional force (f) acting on the sphere is
View SolutionA block of weight W is kept on a rough horizontal surface (friction coefficient μ). Two forces W/2 each are applied as shown in the choose the correct statement
 .
.
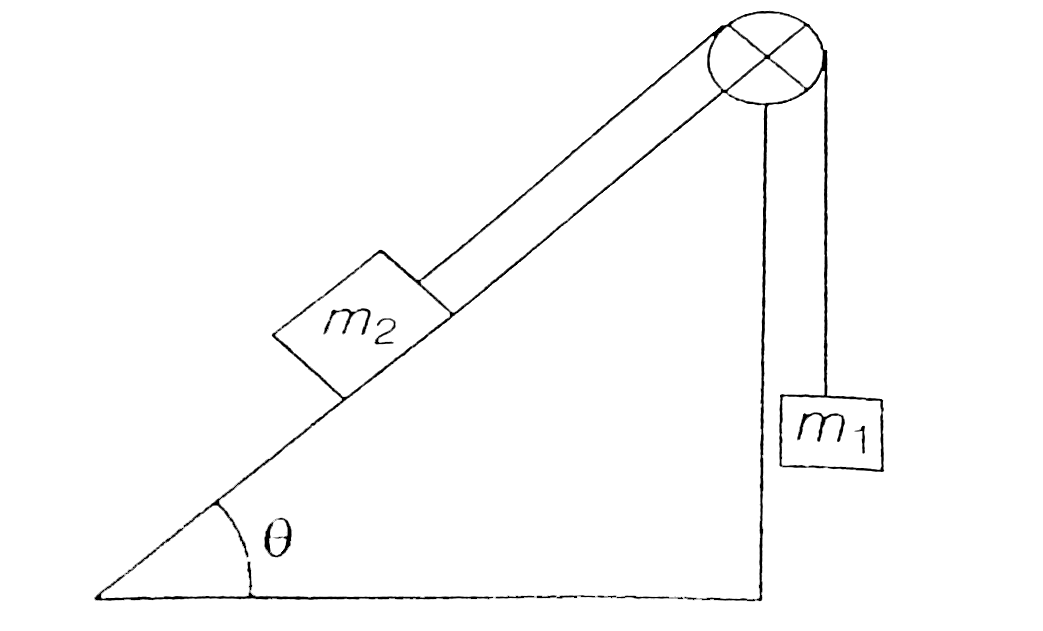
View SolutionIn the figure shown if coefficient of friction is μ, then m2 will start moving upwards if
View SolutionA ring of mass M and radius R is released on an inclined as shown. If the coefficient of friction μ<12tanθ, then during a displacement l:
View Solution
