A diatomic molecule has atoms of masses m1 and m2. The potential energy of the molecule for the interatomic separation r is given by V(r)=−A+B(r−r0)2, where r0 is the equilibrium separation, and A and B are positive constants. the atoms are compressed towards each other from their equilibrium positons and released. what is the vibrational frequency of the molecule?
The correct Answer is:A, B
Figure
Similar Questions
If the potential energy between two molecules is given by U=−Ar6+Br12 , then at equilibrium , separation between molecules , and the potential energy are :
View SolutionIf the potential energy between two molecules is given by U=−Ar6+Br12 , then at equilibrium , separation between molecules , and the potential energy are :
View Solution
Knowledge Check
- Question 1 - Select One
The potential energy U of diatomic molecules as a function of separation r is shown in figure. Identify the correct stateement.
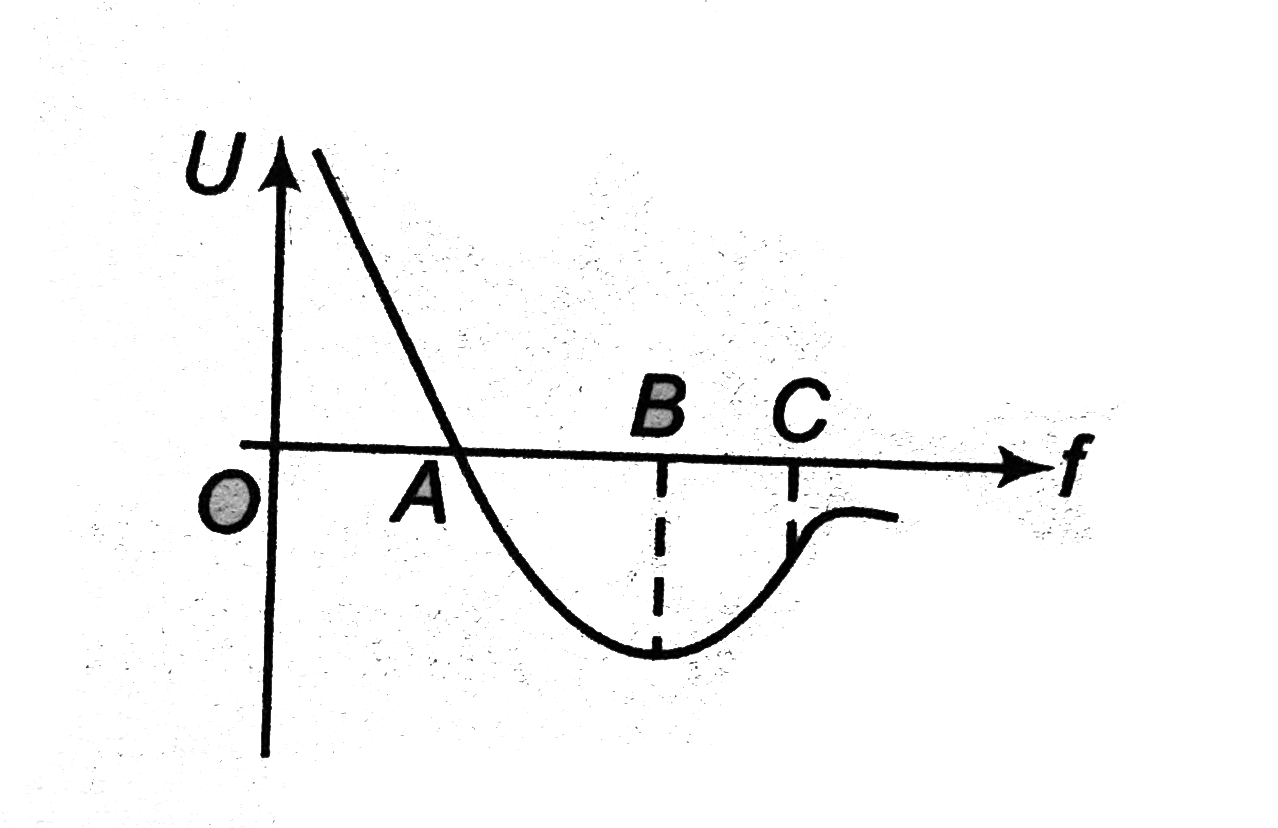 AThe atoms are in equilibrium if r=OABThe force is repulsive only if r lies between A and BCThe force is attractive if r lies between A and BDThe atoms are in equilibrium if r=OB
AThe atoms are in equilibrium if r=OABThe force is repulsive only if r lies between A and BCThe force is attractive if r lies between A and BDThe atoms are in equilibrium if r=OB - Question 2 - Select One
Potential energy in a field is given by U=−Ar6+Br11 then find the value of r for equilibrium position.
Ar=(6A11B)15Br=(11B6A)15Cr=(6B11A)15Dr=(11A6B)15
The potential energy U of diatomic molecules as a function of separation r is shown in figure. Identify the correct stateement.
 View Solution
View SolutionThe potential energy of a two particle system separated by a distance r is given by U(r)=Ar where A is a constant. Find to the radial force Fr, that each particle exerts on the other.
View SolutionThe potential energy of a two particle system separated by a distance r is given by U(r)=Ar where A is a constant. Find to the radial force Fr, that each particle exerts on the other.
View SolutionThe potential energy of a particle in a certain field has the form U=(a/r2)−(b/r) , where a and b are positive constants and r is the distance from the centre of the field. Find the value of r0 corresponding to the equilibrium position of the particle, examine whether this position is stable.
View SolutionThe potential energy of a particle in a certain field has the form U=(a/r2)−(b/r) , where a and b are positive constants and r is the distance from the centre of the field. Find the value of r0 corresponding to the equilibrium position of the particle, examine whether this position is stable.
View SolutionPotential energy in a field is given by U=−Ar6+Br11 then find the value of r for equilibrium position.
View Solution

