The electric field intensity due to a thin infinity long straight wire of uniform linear charge density λ at O is-
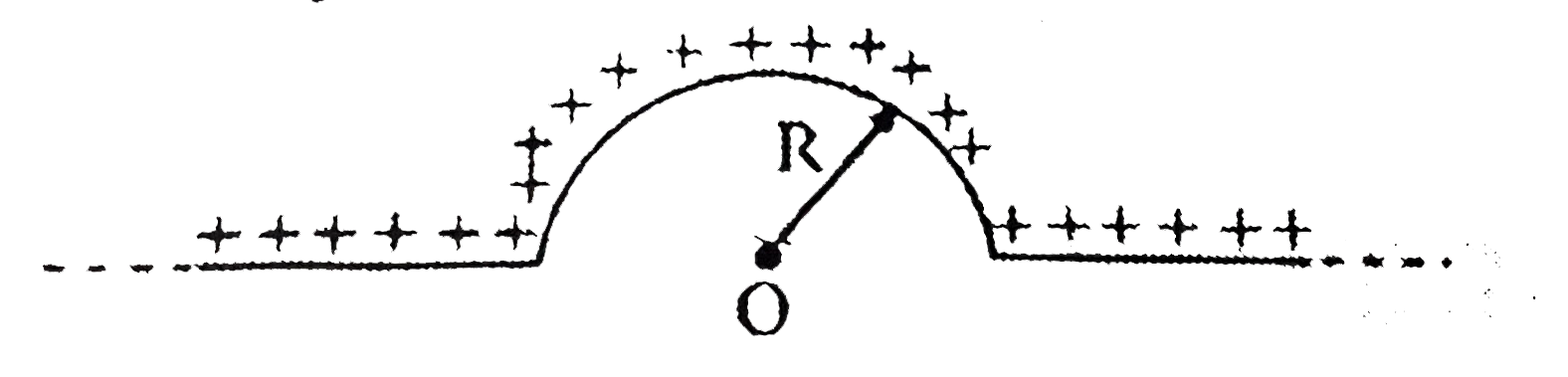
λ2πε0R
λ√22πε0R
λ√52πε0R
zero
The correct Answer is:A
Earc=2kλrsin.θ2
=2kλrsin.180∘2
=λ2πε0R
Topper's Solved these Questions
Similar Questions
State Gauss' law in electrostatic. Using it derive an expression for the electric field due to an infinitely long straight wire of linear charge density λ C/m.
View SolutionWrite the expression of electric field due to an infinitely long, straight, wire having linear charge density λ at a point that is at a distance r from it.
View Solution
Knowledge Check
Electric field of an infinitely long straight wire is proportional to:
ArB1r2C1r3D1r
State Gauss's law in electrostatics. Use this law to derive an expression for the electric field due to an infinitely long straight wire of linear charge density λcm−1
View SolutionState Gauss' law.Using this law obtain the expression for the electric field due to an infinitely long straight conductor of linear charge density λ
(ii) A wire AB of length L has linear charge λ=kx, where x is measured from the end A of the wire. The wire is enclosed by a Gaussian hollow surface.Find the expression for the electric flux through the surface.
View SolutionObtain the formula for the electric field due to a long thin wire of uniform linear charge density λ without using Gauss's law. [Hint. use Coulomb's law directly and evaluate the necessary integral].
View SolutionObtain the formula for the electric field due to a along thin wire of uniform linear charge density λ without using Gauss's law.
View SolutionState Gauss's law on electrostatics and derive an expression for the electric field due to a long straight thin uniformly charged wire (linear charge density ) at a point lying at a distance r from the wire.
View SolutionWhat is the electric field intensity at any point on the axis of a charged rod of length 'L' and linear charge density λ? The point is separated from the nearer end by a.
View SolutionDetermine electric field intensity near an infinitely long straight uniformly charge wire.
Or.
Using Gauss' law expression for electric field intensity at a point situated at a distance 'r' from an infinitely long, uniformly charged straight wire.
View Solution
