Derive an expression for the electric potential at any point P at a distance r from the center of an electric dipole, making angle α with its axis.
Step by step video & image solution for Derive an expression for the electric potential at any point P at a distance r from the center of an electric dipole, making angle alpha with its axis. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
(a) Derive the expression for the electric potential at any point P, at distance r from the centre of an electric dipole, making angle α, with its axis.
(b) Two point charges 4μCand+1μC are separated by a distance of 2m in air. Find the point on the line joining charges at which the net electric field of the system is zero.
View SolutionDerive an expression for the electric potential at any point along the axial line of an electric dipole.
View Solution
Knowledge Check
At a point on the axis of an electric dipole
Athe electric field E is zeroBthe electric potential V is zeroCboth E and V are zeroDneither E nor V is zeroThe electric field of an electric dipole at a point on its axis , at a distance d from the center of the dipole, varies as
A1dB1d2C1d3D1d32
Derive the expression for the electric potential at any point along the axial line of an electric dipole.
View SolutionWhat is the electric potential at a point P, distance r from the mid-point of ann electric dipole of moment p(=2aq) ?
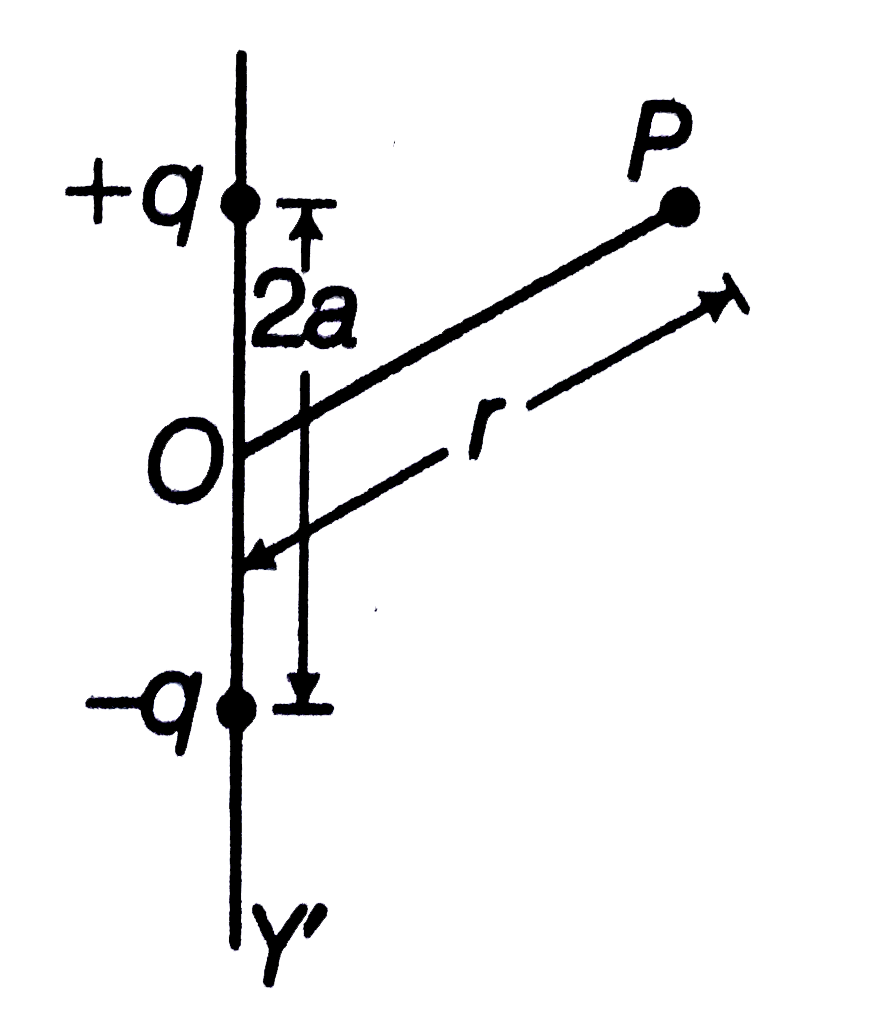
View SolutionThe electric field at a point at a distance r from an electric dipole is proportional to ......
View SolutionDerive an expression for the electric field at any point along the axial line of an electrical dipole.
View SolutionDeive an expression for the electric field at any point on the equatorial line of an electric dipole.
View SolutionA thin circular ring of radius r is charged uniformly so that its linear charge density becomes λ . Derive an expression for the electric field at a point P at a distance x from it along the axis of the ring. Hence, prove that at large distances (r >> r), the ring behaves as a point charge.
View Solution
