A thin circular ring of radius r is charged uniformly so that its linear charge density becomes $λ$ . Derive an expression for the electric field at a point P at a distance x from it along the axis of the ring. Hence, prove that at large distances (r $> >$ r), the ring behaves as a point charge.

Text Solution

Verified by Experts

Let a thin circular ring of radius . is charged unifornmly having a linear charge density $λ$ .. Let Pbe a point on the axis of the ring at a distance .x. from its centre. Consider an element of length Al around a point A of the ring carrying a charge $Δ q = λ Δ I$ Electric field at point P due to this charge element is
$∣ ∣ Δ \to E ∣ ∣ = \frac{1}{4 π \in_{0}} . \frac{Δ q}{{(A P)}^{2}} = \frac{1}{4 π \in_{0}} . \frac{λ Δ I}{(x^{2} + x^{2})}$

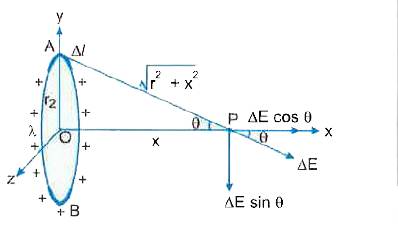
The electric field is directed along AP and thus subtends an angle 0 with the axis of the ring and can be resolved into two components (i) $Δ E$ cos $θ$ along the axis, and (ii) $Δ E$ sin $θ$ normal to the axis of ring. It is clear from symmetry that normal components $Δ E$ sin $θ$ . due to mutually opposite charge elements (say A and B) nullify each other, but their axial components $. Δ E cos θ$ are added up.
$∴$ Net electric field at point P due to whole charged ring will be
$E = \sum Δ E cos θ = \sum \frac{1}{4 π \in_{0}} . \frac{λ Δ l}{(r^{2} + x^{2})} . \frac{x}{\sqrt{r^{2} + x^{2}}}$
$= \frac{λ x}{4 π \in_{0} {(r^{2} + x^{2})}^{3 / 2}} \sum Δ I = \frac{λ . x}{4 π \in_{0} {(r^{2} + x^{2})}^{3 / 2}} .2 π r$
$= \frac{λ r x}{2 \in_{0} {(r^{2} + x^{2})}^{3 / 2}}$
The field $\to E$ is directed along the axis OP of the charged ring If x $> >$ r, then the above relation may be written as
$E = \frac{λ r x}{2 \in_{0} {(x^{2})}^{3 / 2}} = \frac{λ r}{2 \in_{0} x^{2}}$
As total charge on the ring q = $λ .2 π r$ so $λ r = \frac{q}{2 π}$ and hence E = $\frac{q}{4 π \in_{0} x^{2}}$
The above relation shows that electric field is same as that due to a point charge q situated at the centre of ring ie., the charged ring is now behaving as a point charge.

Updated on:21/07/2023

A ring of radius $a$ contains a charge $q$ distributed uniformly over its length. Find the electric field at a point on the axis of the ring at a distance $x$ from the centre.
A $\frac{k q^{2}}{x {(a^{2} + x^{2})}^{\frac{3}{2}}}$
B $\frac{2 k q^{2} x}{{(a^{2} + x^{2})}^{\frac{3}{2}}}$
C $\frac{k q^{2} x}{{(a^{2} + x^{2})}^{\frac{3}{2}}}$
D $\frac{k q^{2}}{2 x {(a^{2} + x^{2})}^{\frac{3}{2}}}$