Two small spheres of masses $M_{1}$ and $M_{2}$ are suspended by weightless insulating threads of lengths $L_{1}$ and $L_{2}$ . The speres carry charges $Q_{1}$ and $Q_{2}$ respectively. The spheres are suspended such that they are in level with one another adn the threads are inclined to the verticle at angles $θ_{1}$ and $θ_{2}$ respectively . Which one of the following conditions is essential for $θ_{1} = θ_{2}$ ?

A

$M_{1} \neq M_{2}$ , but $Q_{1} = Q_{2}$

B

$Q_{1} = Q_{2}$

C

$L_{1} = L_{2}$

D

$M_{1} = M_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Refer to Fig.

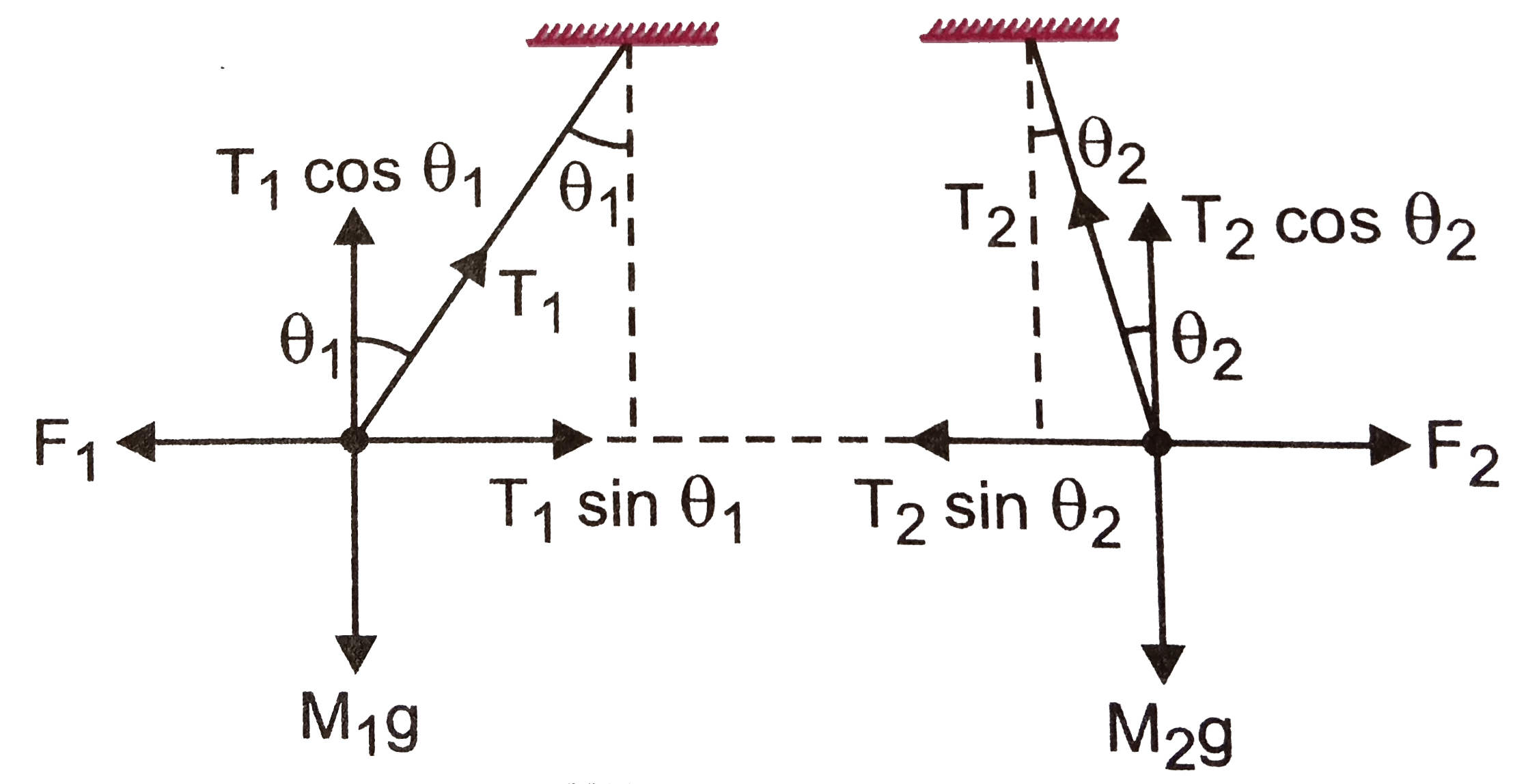
Sphere $1$ will be in equilibrium, when $T_{1} {cos θ}_{1} = M_{1} g$ and $T_{1} {sin θ}_{1} = F_{1}$
$∴ {tan θ}_{1} = \frac{F_{1}}{M_{1} g}$
Similarly, sphere 2 will be in equilibrium, when
$T_{2} {cos θ}_{2} = M_{2} g$ and $T_{2} {sin θ}_{2} = F_{2}$
$∴ {tan θ}_{1} = \frac{F_{2}}{M_{1} g}$
As charges repel eachother with the same force, therefore $F_{1} = F_{2}$ For $θ_{1} = θ_{2}, M_{1} = M_{2}$ .

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two small spheres with mass $m_{1}$ and $m_{2}$ hang from massless insulating threads of length $l_{1}$ and $l_{2}$ . The two spheres carry charges $q_{1}$ and $q_{2}$ respectively. The spheres are hung such that they are on the same horizontal level and the threads are inclined to the vertical at angles $θ_{1}$ and $θ_{1}$ . Which of the condition is required if $θ_{1} = θ_{2}$ ?

AIf $m_{1} = m_{2}$
B $| q_{1} | = | q_{2} |$
C $l_{1} = l_{2}$
D $\frac{q_{1}}{m_{1}} = \frac{q_{2}}{m_{2}}$
Question 2 - Select One
The insulated spheres of radii $R_{1}$ and $R_{2}$ having charges $Q_{1}$ and $Q_{2}$ respectively are connected to each other. There is
ANo change in the energy of the system
BAn increase in the energy of the system
CAlways a decrease in the energy of the system
DA decrease in the energy of the system unless
$Q_{1} R_{2} = Q_{2} R_{1}$
Question 3 - Select One
Two positively charged sphere of masses $m_{1}$ and $m_{2}$ are suspended from a common point at the ceiling by identical insulating massless strings of length $l$ . Charges on the two spheres are $q_{1}$ and $q_{2}$ respectively. Equilibrium both strings make the same angle $θ$ with the vertical. then
A $q_{1} m_{2} = q_{2} m_{2}$
B $m_{1} = m_{2}$
C $m_{1} = m_{2} sin θ$
D $q_{2} m_{1} = q_{1} m_{2}$

PRADEEP-ELECTROSTATICS-Exercise

Home
Ask Doubt
Profile